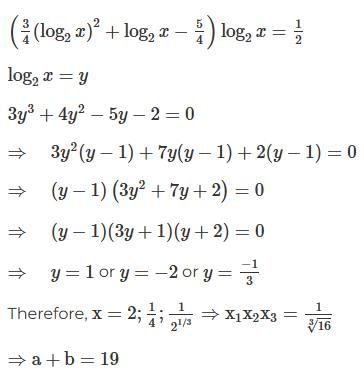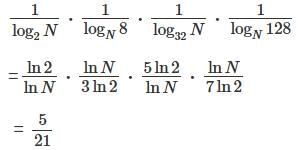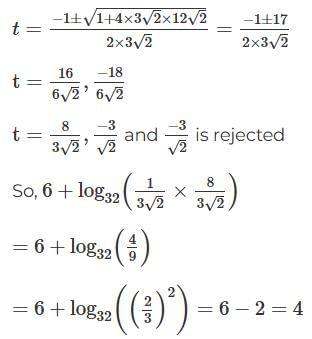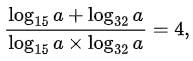Solved Examples: Logarithms | Quantitative Aptitude (Quant) - CAT PDF Download
Q1: If the product of the roots of the equation, 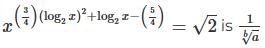 where a, b ∈ N, then the value of (a+b)
where a, b ∈ N, then the value of (a+b)
A: 0
B: 1
C: 18
D: 19
Ans: D
Sol:
Take the log on both sides with base 2
Concept used: Converting exponential form into log form, applying Vieta’s relation (product of roots).
Q2: For 0 < a ≠ 1, find the number of ordered pair (x,y) satisfying the equation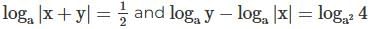
A: 0
B: 1
C: 2
D: 4
Ans: C
Sol:
If x > 0, then x = a/3, y = 2a/3
If x < 0, then y = 2a, x = −a
Therefore, possible ordered pairs = (a/3, 2a/3) and (−a, 2a)
Concept used: Splitting into cases based on positivity/negativity of x, and solving simple linear equations in logs.
Q3: For N > 1, the product  simplifies to
simplifies to
A: 3/7
B: 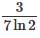
C: 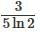
D: 5/21
Ans: D
Sol:
Concept used: Using properties of logarithms and telescoping product simplification.
Q4: The value of the expression (log₁₀2)³ + log₁₀8 ⋅ log₁₀5 + (log₁₀5)³ is
A: rational which is less than 1
B: rational which is greater than 1
C: equal to 1
D: an irrational number
Ans: C
Sol:
log₁₀2 = a and log₁₀5 = b
⇒ a + b = 1; a³ + 3ab + b³ = ?
Now (a + b)³ = 1 ⇒ a³ + b³ + 3ab = 1
Concept used: Substitution (let log₂ = a, log₅ = b), then using expansion (a+b)³ = a³+b³+3ab to simplify.
Q5: The value of  is
is
A: 1
B: 2
C: -4
D: 4
Ans: D
Sol:
Concept used: Change of base formula & log identities (log a – log b = log (a/b), etc.).
Q6: For a real number x, if 1/2, 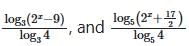 are in arithmetic progression, then the common difference is
are in arithmetic progression, then the common difference is
A: log4 (3/2)
B: log4 (7/2)
C: log4 7
D: log4(23/2)
Ans: B
Sol:
Given 1/2,are in arithmetic progression,
⇒ 1/2, log₄(2x - 9), and log₄(2x + 17/2) are in AP
⇒ 2 log4(2x - 9) = 1/2 + log4(2x + 17/2)
⇒ log4(2x - 9)² = log₄ 2 + log4(2x + 17/2)
⇒ log4(2x - 9)² = log4 2 + log4(2x + 17/2)
⇒ log4(2x - 9)² = log4 2 × (2x + 17/2)
⇒ (2x - 9)² = 2 × (2x + 17/2) [Assuming 2^x = a]
⇒ a² - 18a + 81 = 2a + 17
⇒ a² - 20a + 64 = 0
⇒ (a - 16)(a - 4) = 0
⇒ a = 2x = 16 [4 is rejected as (a - 9) cannot be negative]
Now the first term of the AP = 1/2 and
second term of the AP = log4 (2x - 9) = log4 (16 - 9) = log4 7
Common difference = log4 7 - 1/2 = log4 7 - log4 2 = log4 7/2
Hence, option (a).
Concept used: Setting terms in AP, applying log properties, the quadratic equation for validity, and then finding the common difference.
Q7: For real number a, if 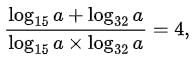 then a must lie in the range
then a must lie in the range
A: 4 < a < 5
B: 2 < a < 3
C: a = 5
D: 3 < a < 4
Ans: A
Sol:
Converting all logs to base 10.
⇒ loga32 + loga15 = 4
⇒ loga(32 × 15) = 4
⇒ a4 = 480
This is possible when 4 < a < 5.
Hence, option (a).
Concept used: Converting to base-10 log, multiplying inside, checking possible range for a (inequalities in log domain).
Q8: If loga30 = A, loga(5/3) = -B and log2a = 1/3, then log3a equals
A: (A + B)/2 - 3
B: 2/(A + B) - 3
C: 2/(A + B - 3)
D: (A + B - 3)/2
Ans: C
Sol:
Since all the 4 options have A + B, lets add A and B.
∴ A + B = loga30 + (-loga(5/3))
= loga30 – loga(5/3) = loga(30 × 3/5)
= loga(18) = loga(2 × 32)
⇒ A + B = loga(2) + 2loga(3)
⇒ A + B = 3 + 2loga(3) [∵ log2a = 1/3 ∴ loga2 = 3]
⇒ loga(3) = (A + B - 3)/2
⇒ log3(a) = 2/(A + B - 3)
Hence, option (c).
Concept used: Using log addition/subtraction rules, substitution, and base conversion to rewrite log(a).
Q9: If p³ = q⁴ = r⁵ = s⁶, then the value of logₛ(pqr) is equal to
A: 47/10
B: 16/5
C: 24/5
D: 1
Ans: A
Sol:
Given, p³ = q⁴ = r⁵ = s⁶ = k
⇒ p³ = k
⇒ p = k¹/³
Similarly,
q = k¹/⁴
r = k¹/⁵
s = k¹/⁶
pqr = k¹/³ × k¹/⁴ × k¹/⁵ = k¹/³ + ¹/⁴ + ¹/⁵ = k⁴⁷/⁶⁰
Now, logₛ(pqr) = logₖ₁/₆ k⁴⁷/⁶⁰ = 47/10
Hence, option (a).
Concept used: Expressing variables in terms of k, multiplying powers, simplifying to single exponent, applying change of base for log.
Q10: The smallest integer n for which 4ⁿ > 17¹⁹ holds, is closest to
A: 33
B: 37
C: 39
D: 35
Ans: C
Sol:
We have, 4ⁿ > 17¹⁹
Taking log on both sides to the base 4,
n × log₄ 4 > 19 × log₄ 17
Now, 17 > 4².
∴ log₄ 17 > 2.
⇒ n × log₄ 4 > 19 × log₄ 17 > 19 × 2
Also, log₄ 4 = 1
∴ n > 38.
Hence, option (c).
Concept used: Taking the log (base 4), comparing the exponent with the benchmark value, and deducing the minimum integer n.
|
167 videos|229 docs|95 tests
|
FAQs on Solved Examples: Logarithms - Quantitative Aptitude (Quant) - CAT
| 1. What are logarithms and how are they used in mathematics? |  |
| 2. How do you convert a logarithmic equation to its exponential form? |  |
| 3. What are common types of logarithms used in mathematics? |  |
| 4. How do logarithmic properties help in solving logarithmic equations? |  |
| 5. What is the significance of the logarithm of 1 and the logarithm of the base? |  |