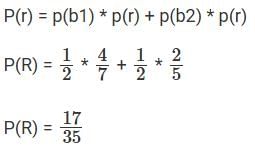Solved Examples: Permutations and Combinations | Quantitative Aptitude (Quant) - CAT PDF Download
 Q1: All 5-letter words formed from "CRANE" (no repetition) are listed alphabetically. What is the rank of "RANCE"?
Q1: All 5-letter words formed from "CRANE" (no repetition) are listed alphabetically. What is the rank of "RANCE"?
A: 92
B: 74
C: 86
D: 99
Ans: D
Sol:
Total words = 5! = 120.
Words starting with A, C, E, N: 4 × 4! = 96.
Next, RA ___: 3! = 6 words (RACNE, RACEN, RANCE, RANEC, RAECN, RAENC).
"RANCE" is the 3rd word in this subset.
Rank = 96 + 3 = 99
Q2: How many 4-digit numbers can be formed using {1, 2, 3, 4, 5} with at least one digit repeated?
A: 505
B: 500
C: 600
D: 625
Ans: A
Sol:
Total numbers = 5 × 5 × 5 × 5 = 625.
Numbers with all distinct digits = 5 × 4 × 3 × 2 = 120.
Answer = 625 − 120 = 505 (A).
Q3: What is the sum of all 4-digit numbers formed by rearranging 1, 2, 3, 4?
A: 66,660
B: 65,000
C: 64,440
D: 60,000
Ans: A
Sol:
Each digit appears 6 times in each place.
Sum = 6×(1+2+3+4)×(1000+100+10+1)
= 66,660 (A).
Q4: How many numbers between 1 and 300 are divisible by 3, 5, or 7?
A: 180
B: 162
C: 120
D: 140
Ans: B
Sol:
|A∪B∪C| = |A| + |B| + |C| − |A∩B| − |A∩C| − |B∩C| + |A∩B∩C|
|A| = numbers divisible by 3
|B| = numbers divisible by 5
|C| = numbers divisible by 7
= 100 + 60 + 42 − 20 − 14 − 8 + 2 = 162
Q5: Find the sum of all 4-digit numbers formed by rearranging 1123.
A: 28,444
B: 29,332
C: 28,886
D: 27,776
Ans: C
Sol:
Total permutations = 4! / 2! = 12.
Digit contributions:
1: 6 times, 2: 4 times, 3: 4 times.
Sum = (6×1 + 4×2 + 4×3) × 1111 = 26 × 1111 = 28,886.
Q6: What is the sum of all 6-digit numbers formed by rearranging 123456?
A: 279,999,720
B: 241,000,000
C: 215,999,996
D: 229,222,222
Ans: A
Sol:
Each digit appears 120 times in each place (6! / 6 = 120).
Sum = 120 × (1+2+3+4+5+6) × 111,111
= 120 × 21 × 111,111
= 279,999,720
Q7: How many numbers from 1 to 1000 are divisible by 2, 3, 5, or 7?
A: 768
B: 772
C: 780
D: 800
Ans: B
Sol:
Apply 4-set inclusion-exclusion:
A ∪ B ∪ C ∪ D| = |A| + |B| + |C| + |D|
- |A ∩ B| - |A ∩ C| - |A ∩ D| - |B ∩ C| - |B ∩ D| - |C ∩ D|
+ |A ∩ B ∩ C| + |A ∩ B ∩ D| + |A ∩ C ∩ D| + |B ∩ C ∩ D|
- |A ∩ B ∩ C ∩ D|
Where,
|A| = numbers divisible by 2
|B| = numbers divisible by 3
|C| = numbers divisible by 5
|D| = numbers divisible by 7
Total = 500 (2) + 333 (3) + 200 (5) + 142 (7) − 166 (6) − 100 (10) − 71 (14) − 66 (15) − 47 (21) − 28 (35) + 33 (30) + 23 (42) + 14 (70) + 9 (105) − 4 (210) = 772 (B).
Q8: Of 22 points on a plane, 8 are on a straight line, 7 are on another straight line and 10 are on a third straight line. How many triangles can be drawn by connecting some three points from these 22? [2018]
A: 22C3
B: 22C3 - (8C3+ 7C3 +10C3)
C: 22C3 + (8C3+ 7C3 +10C3)
D: 8C3+ 7C3 +10C3
Ans: B
Sol:
From the 22 points on a plane we can form 22C3 triangles but it is given that 8 are on one straight line, 7 are on another straight line and 10 more are on another straight line,
so we can form triangles on joining points which are on straight lines so we have to subtract (8C3+ 7C3 +10C3) from the total.
Hence, we can form 22C3 - (8C3+ 7C3 +10C3) triangles.
Q9: A bag contains 4 red and 3 black balls. A second bag contains 2 red and 3 black balls. One bag is selected at random. If from the selected bag one ball is drawn, then what is the probability that the ball drawn is red?
A: 39/70
B: 41/70
C: 29/70
D: 17/35
Ans: D
Sol:
Let Red balls be 'r' and brown balls be 'b'Hence the answer is option D.
Q10: In how many ways can we rearrange the letters of the word MANANA such that no two A’s are adjacent to each other?
A: 3 ! * 5C3
B: 4 ! * 4C3
C: 3 * 4C3
D: 3 ! * 4C3
Ans: C
Sol:
MANANA has 6 letters, of which 3 are A's
Now, let us place the letters that are not As on a straight line. We have MNN. These can be arranged in 3!/2! = 3 ways.
Now let us create slots between these letters to place the As in.
In order to ensure that no two As are adjacent to each other, let us create exactly one slot between any two letters.
M __N __ N
Additionally, let us add one slot at the beginning and end as well as the As can go there also.
__ M __N __ N __
Now, out of these 4 slots, some 3 can be A. That can be selected in 4C3 ways.
So, total number of words = 3 ! * 4C3 ways.
|
167 videos|229 docs|95 tests
|
FAQs on Solved Examples: Permutations and Combinations - Quantitative Aptitude (Quant) - CAT
| 1. What are permutations and combinations, and how do they differ? |  |
| 2. How do I calculate permutations of a set? |  |
| 3. What is the formula for combinations, and how is it used? |  |
| 4. Can you provide a real-life example of using permutations? |  |
| 5. How do I determine when to use permutations versus combinations? |  |