Solved Examples for JEE: Solutions | Chemistry for JEE Main & Advanced PDF Download
Example 1. The molarity of 20% (W/W) solution of sulphuric acid is 2.55 M. The density of the solution is:
(a) 1.25 g cm-3
(b) 0.125 g L-1
(c) 2.55 g cm-3
(d) unpredictable
Ans. (a)
Solution.
Volume of 100 g of solution = 100/d ml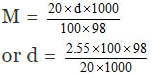
= 1.249 ≈ 1.25
Example 2. The density of a solution containing 13% by mass of sulphuric acid is 1.09 g/mL. Calculate the molarity and normality of the solution-
(a) 1.445 M
(b) 14.45 M
(c) 144.5 M
(d) 0.1445 M
Ans. (a)
Solution.
Volume of 100 gram of the solution = 100/d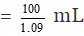
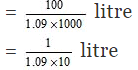
Number of moles of H2SO4 in 100 gram of the solution = 13/98
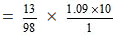
= 1.445 M
Example 3. Calculate the molarity of pure water (d = 1g/L)
(a) 555 M
(b) 5.55 M
(c) 55.5 M
(d) None
Ans. (c)
Solution.
Consider 1000 mL of water
Mass of 1000 mL of water
= 1000 × 1 = 1000 gram
Number of moles of water = 100/18
= 55.5
= 55.5/1
= 55.5 M
Example 4. Calculate the quantity of sodium carbonate (anhydrous) required to prepare 250 ml of 0.1 M solution-
(a) 2.65 gram
(b) 4.95 gram
(c) 6.25 gram
(d) None
Ans. (a)
Solution.
We know that
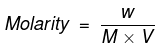
where;
W = Mass of Na2CO3 in gram
M = Molecular mass of Na2CO3 in grams = 106
V = Volume of solution in litres = 250/1000 = 0.25
Molarity = 1/10
Hence, = 1/10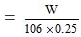
or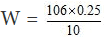
= 2.65 gram
Example 5. The freezing point of a 0.08 molal aqueous solution of NaHSO4 is -0.372°C. The dissociation constant for the reaction
HSO4- ⇌ HSO42-is
(a) 4 × 10-2
(b) 8 × 10-2
(c) 2 × 10-2
(d) 1.86 × 10-2
Ans. (a)
Solution.
ΔTf = Kf × m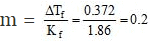
This means that total molal conc. of all particles is 0.2.
NaHSO4 → Na+ + HSO4-
0.08 0.08
HSO4- ⇌ H+ + SO42-
(0.08 - x) x x
The net particle concentration
0.087 = (0.08 - x) + x + x = 0.2
or x = 0.04
Example 6. Find the molality of H2SO4 solution whose specific gravity is 1.98 g ml-1 and 95% by volume H2SO4
(a) 7.412
(b) 8.412
(c) 9.412
(d) 10.412
Ans. (c)
Solution.
H2SO4 is 95% by volume
wt. of H2SO4 = 95g
Vol of solution = 100ml
Moles of H2SO4 = , and weight of solution = 100 × 1.98 = 198 g
Weight of water = 198 - 95 = 103 g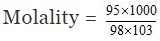
= 9.412
Hence molality of H2SO4 solution is 9.412
Example 7. Calculate molality of 1 litre solution of 93% H2SO4 by volume. The density of solution is 1.84 gm ml-1
(a) 9.42
(b) 10.42
(c) 11.42
(d) 12.42
Ans. (b)
Solution.
Given H2SO4 is 93% by volume
wt. of H2SO4 = 93g
Volume of solution = 100ml
weight of solution = 100 × 1.84 gm
= 184 gm
wt. of water = 184 - 93 = 91 gm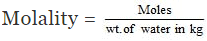
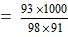
= 10.42
Example 8. Suppose 5gm of CH3COOH is dissolved in one litre of Ethanol. Assume no reaction between them. Calculate molality of resulting solution if density of Ethanol is 0.789 gm/ml.
(a) 0.0856
(b) 0.0956
(c) 0.1056
(d) 0.1156
Ans. (c)
Solution.
 Fig: Acetic acid structure
Fig: Acetic acid structure
Wt. of CH3COOH dissolved = 5g
Eq. of CH3COOH dissolved = 5/60
Volume of ethanol = 1 litre = 1000ml.
Weight of ethanol = 1000 × 0.789 = 789g
Molality of solution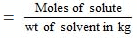
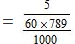
= 0.1056
Example 9. Calculate the molarity and normality of a solution containing 0.5 gm of NaOH dissolved in 500 ml. solution-
(a) 0.0025 M, 0.025 N
(b) 0.025 M, 0.025 N
(c) 0.25 M, 0.25 N
(d) 0.025 M, 0.0025 N
Ans. (b)
Solution.
Wt. of NaOH dissolved = 0.5 gm
Vol. of NaOH solution = 500 ml
Calculation of molarity
0.5 g of NaOH = 0.5/40 moles of NaOH
[∴ Mol. wt of NaOH = 40]
= 0.0125 moles
Thus 500 ml of the solution contain NaOH = 0.0125 moles
1000 ml of the solution contain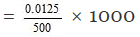
= 0.025 M
Hence molarity of the solution = 0.025 M
Calculation of normality
Since NaOH is monoacidic;
Eq. wt. of NaOH = Mol. wt. of NaOH = 40
0.5 gm of NaOH = 0.5/40 gm equivalents = 0.0125 gm equivalents
Thus 500 ml of the solution contain NaOH = 0.0125 gm equ.
1000 ml of the solution contain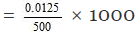
Hence normality of the solution = 0.025 N
Example 10. Calculate the molality and mole fraction of the solute in aqueous solution containing 3.0 gm of urea per 250 gm of water (Mol. wt. of urea = 60).
(a) 0.2 m, 0.00357
(b) 0.4 m, 0.00357
(c) 0.5 m, 0.00357
(d) 0.7m, 0.00357
Ans. (a)
Solution.
Wt. of solute (urea) dissolved = 3.0 gm
Wt. of the solvent (water) = 250 gm
Mol. wt. of the solute = 60
3.0 gm of the solute = 3.0/60 moles = 0.05 moles
Thus 250 gm of the solvent contain = 0.05 moles of solute
1000 gm of the solvent contain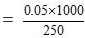
= 0.2 moles
Hence molality of the solution = 0.2 m
In short,
Molality = No. of moles of solute/1000 g of solvent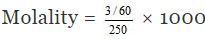
= 0.2 m
Calculation of mole fraction
3.0 gm of solute = 3/60 moles = 0.05 moles
250 gm of water = 250/18 moles = 13.94 moles
Mole fraction of the solute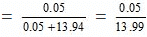
= 0.00357
Example 11. A solution has 25% of water, 25% ethanol and 50% acetic acid by mass. Calculate the mole fraction of each component.
(a) 0.50, 0.3, 0.19
(b) 0.19, 0.3, 0.50
(c) 0.3, 0.19, 0.50
(d) 0.50, 0.19, 0.3
Ans. (d)
Solution.
Since 18 g of water = 1 mole
25 g of water = 25/18 = 1.38 mole
Similarly, 46 g of ethanol = 1 mole
25 g of ethanol = 25/46 = 0.55 moles
Again, 60 g of acetic acid = 1 mole
50 g of acetic acid = 50/60 = 0.83 mole
Mole fraction of water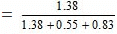
= 0.50
Similarly, Mole fraction of ethanol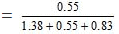
= 0.19
Mole fraction of acetic acid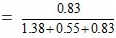
= 0.3
Example 12. 15 gram of methyl alcohol is dissolved in 35 gram of water. What is the mass percentage of methyl alcohol in solution?
(a) 30%
(b) 50%
(c) 70%
(d) 75%
Ans. (a)
Solution.
Total mass of solution = (15 35) gram = 50 gram
mass percentage of methyl alcohol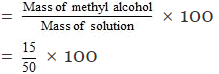
= 30%
Example 13. Calculate the masses of cane sugar and water required to prepare 250 gram of 25% cane sugar solution?
(a) 187.5 gram, 62.5 gram
(b) 62.5 gram, 187.5 gram
(c) 162.5 gram, 87.5 gram
(d) None of these
Ans. (b)
Solution.
Mass percentage of sugar = 25
We know that
Mass percentage
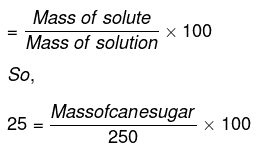
or Mass of cane sugar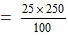
= 62.5 gram
Mass of water = (250 - 62.5) = 187.5 gram
Example 14. The density of a 3M sodium thiosulphate solution (Na2S2O3) is 1.25 g/mL. Calculate
(i) the percentage by mass of sodium thiosulphate,
(ii) the mole fraction of sodium thiosulphate and
(iii) molalities of Na and S2O32-ions -
Solution.
(i) Mass of 1000 mL of Na2S2O3 solution
= 1.25 × 1000 = 1250 g
Mass of Na2S2O3 in 1000 mL of 3M solution
= 3 × Mol. mass of Na2S2O3
= 3 × 158 = 474 g
Mass percentage of Na2S2O3 in solution
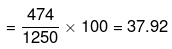
Alternatively,
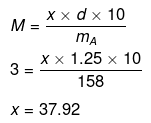
(ii) No. of moles of Na2S2O3 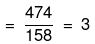
Mass of water = (1250 - 474) = 776 g
No. of moles of water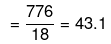
Mole fraction of Na2S2O3
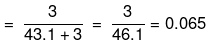
(iii) No. of moles of Na+ ions
= 2 × No. of moles of Na2S2O3
= 2 × 3 = 6
Molality of Na ions
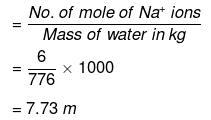
No. of moles of S2 ions = No. of moles of Na2S2O3 = 3
Molality of ions

Example 15. A solution is perpared by dissolving 5.64 gm of glucose in 60g of water. Calculate the following.
(i) mass per cent of each of glucose and water,
(ii) molality of the solution,
(iii) mole fraction of each of glucose and water.
Solution.
(i) Total mass of solution
= 5.64 60 = 65.64 g
Mass per cent of glucose
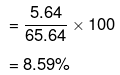
Mass per cent of water
= (100 -Mass per cent of glucose)
= (100 -8.59) = 91.41%
(ii) No. of moles of glucose
=
Mass of water in kg
=
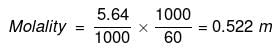
(iii) No. of moles of glucose
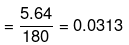
No. of moles of water
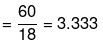
Mole fraction of glucose
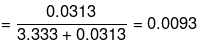
Mole fraction of water
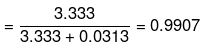
Example 16. The volume of water which must be added to a mixture of 350 cm3 of 6 M HCl and 650 ml of 3 M HCl to get a resulting solution of 3 M concentration is [Ans. D]
(a) 75 mL
(b) 150 mL
(c) 100 mL
(d) 350 mL
Ans. (d)
Solution.
Molarity of mixture of 6 M and 3 M HCl
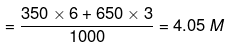
Now, apply dilution formula
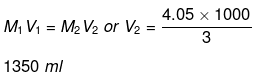
Volume of water to be added
= 1350 - 1000 = 350 ml
Example 17. The mole fraction of CH3OH in an aqueous solution is 0.02 and its density is 0.994 g cm-3. Determine its molarity and molality.
Solution. Let x mole of CH3OH and y mole of water be present in solution.
Mole fraction of CH3OH
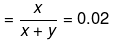
So,

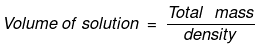
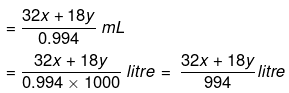
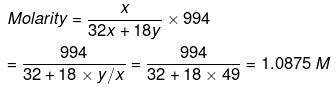
Example 18. Calculate the concentration of NaOH solution in g/mL which has the same normality as that of a solution of HCl of concentration 0.04 g/mL. -
Solution.
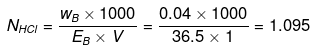
NNaOH º NHCl
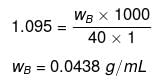
Example 19. How many Na+ ions are present in 50 mL of a 0.5 M solution of NaCl ?
Solution.
Number of moles of NaCl

NaCl → Na+ + Cl¯
Number of moles Na = Number of moles of NaCl = 0.025
Number of ions of Na = 0.025 × 6.023 × 1023 = 1.505 × 1022
Example 20. 250 mL of a Na2CO3 solution contains 2.65 g of Na2CO3. 10 mL of this solution is added to x mL of water to obtain 0.001 M Na2CO3 solution. The value of x is :
(Molecular mass of Na2CO3 = 106 amu)-
(a) 1000
(b) 990
(c) 9990
(d) 90
Ans. (b)
Solution.
Molarity of solution

M1V1 = M2V2
0.1 × 10 = 0.001 (10 x)
x = 990 mL
Example 21. The volumes of two HCl solutions A (0.5 N) and B (0.1 N) to be mixed for preparing 2 L of 0.2 N HCl are -
(a) 0.5 L of A 1.5 L of B
(b) 1.5 L of A 0.5 L of B
(c) 1 L of A 1 L of B
(d) 0.75 L of A 1.25 L of B
Ans. (a)
Solution.
Let x L of A and (2 -x) L of B are mixed.
M1V1 M2V2 = MR (V1 V2)
0.5 × x 0.1 (2 -x) = 0.2 × 2
(0.5 -0.1) x = 0.4 -0.2
0.4 x = 0.2
x = 0.5 L
0.5 L of A and 1.5 L of B should be mixed.
Example 22. Lowering of vapour pressure due to a solute in 1 molal aqueous solution at 100ºC is -
(a) 13.44 mm Hg
(b) 14.12 mm Hg
(c) 31.2 mm Hg
(d) 35.2 mm Hg
Solution.
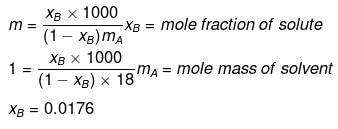
xA = 1 -0.0176 = 0.9824
p = p°xA
= 760 × 0.9824 = 746.62
Dp = p° - p = 760 -746.62
= 13.4
Example 23. The mass of a non-volatile solute (molecular mass = 40) which should be dissolved in 114 g octane to reduce its vapour pressure to 80% will be -
(a) 20 g
(b) 30 g
(c) 10 g
(d) 40 g
Ans. (c)
Solution.
If p° = 100, then p = 80
p = p° xA
80 = 100 × xA
xA = 0.80
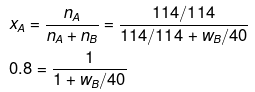
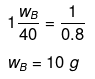
Example 24. A solution of urea in water has boiling point of 100.15ºC. Calculate the freezing point of the same solution if Kf and Kb for water are 1.87 K kg mol-1 and 0.52 K kg mol-1 respectively -
Solution.
ΔTb = (100.15 -100) = 0.15ºC
We know that, ΔTb = molality × Kb
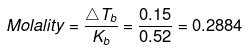
ΔTf = molality × Kf
= 0.2884 × 1.87 = 0.54ºC
Thus, the freezing point of the solution
= -0.54ºC.
Example 25. Calculate the molal depression constant of a solvent which has freezing point 16.6ºC and latent heat of fusion 180.75 J g-1 -
Solution.
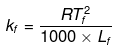
R = 8.314 J K-1 mol-1,
Tf = 16.6ºC = 273 16.6 = 289.6 K,
Lf = 180.75 J g-1
Substituting the values in the above equation,
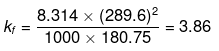
Example 26. The freezing point depression of 0.001 m Kx[Fe(CN)6 ] is 7.10 × 10-3 K. Determine the value of x. Given, Kf = 1.86 K kg mol-1 for water -
Solution. Dx = i × Kf × m
7.10 × 10-3 = i × 1.86 × 0.001
i = 3.817
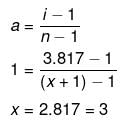
Molecular formula of the compound is
K3 [Fe(CN)6]
Example 27. A certain substance `A' tetramerises in water to the extent of 80%. A solution of 2.5 g of A in 100 g of water lowers the freezing point by 0.3ºC. The molar mass of A is -
(a) 122
(b) 31
(c) 244
(d) 62
Ans. (d)
Solution.
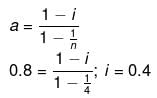
ΔT = iKf × m
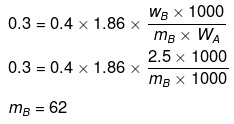
Example 28. van't Hoff factor of Hg2Cl2 in its aqueous solution will be (Hg2Cl2 is 80% ionized in the solution) -
(a) 1.6
(b) 2.6
(c) 3.6
(d) 4.6
Ans. (b)
Solution. 
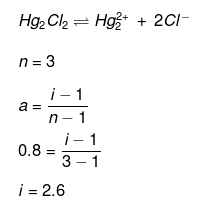
Example 29. Calculate the amount of NaCl which must be added to 100 g water so that freezing point is depressed by 2K. For water, Kf = 1.86 K kg mol-1 -
Solution. NaCl is a strong electrolyte. It is completely dissociated in solution.
Degree of dissociation, a = 1
NaCl Na+1 Cl-1
(n = 2)
No. of particles after dissociation = 1 (n -1) a
= 1 (2 -1) × 1 = 2
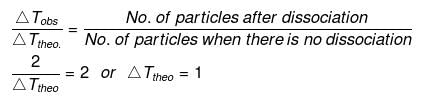
Let w g of NaCl be dissolved in 100 g of water.
So,
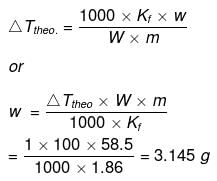
Example 30. The degree of dissociation of Ca(NO3)2 in a dilute solution containing 14 g of the salt per 200 g of water at 100ºC is 70%. If the vapour pressure of water is 760 mm, calculate the vapour pressure of solution -
Solution. Dptheo. = Lowering in vapour pressure when there is no dissociation
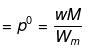
(given, p° = 760 mm, w = 14 g, W = 200 g, M = 18, m = 164)
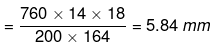
Degree of dissociation
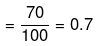
Ca(NO3)2 Ca2+ + 2NO3-
(n = 3)
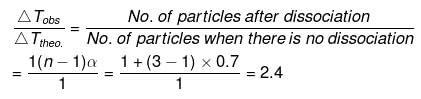
So, ΔTobs. = 2.4 × ΔTtheo. = 2.4 × 5.84
= 14.02 mm
p -ps = Dpobs. = 14.02
ps = ps -14.02 = 760 - 14.02 = 745.98 mm
Example 31. Calculate the normal boiling point of a sample of sea water found to contain 3.5% of NaCl and 0.13% of MgCl2 by mass. The normal boiling point of water is 100ºC and Kb (water) = 0.51 K kg mol-1. Assume that both the salts are completely ionised -
Solution.
Mass of NaCl = 3.5 g
No. of moles of NaCl 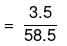
Number of ions furnished by one molecule of NaCl is 2.
So, actual number of moles of particles furnished by sodium chloride = 2 × Similarly, actual number of moles of particles furnished by magnesium chloride
= 3 × Total number of moles of particles
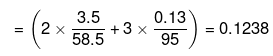
Mass of water = (100 -3.5 -0.13) = 96.37 g
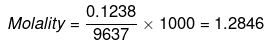
ΔTb = Molality × Kb
= 1.2846 × 0.51 = 0.655 K
Hence, boiling point of sea water = 373.655 K or 100.655ºC.
Example 32. Sea water is 3.5% by mass of a salt and has a density 1.04 g cm-3 at 293 K. Assuming the salt to be sodium chloride, calculate the osmotic pressure of sea water. Assume complete ionization of the salt.
Solution. Mass of NaCl = 3.5 g
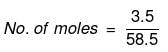
Actual number of moles of particles of solute in solution=
Volume of solution = 1 litre
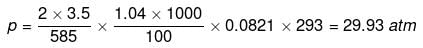
Example 33. Molality of a solution in aqueous medium is 0.8. Calculate its mole fraction and the percentage by mass of solute if molar mass of solute is 60.
Solution. We know that,
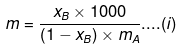
where, xB = mole fraction of solute
mA = molar mass of solvent
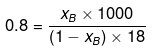
xB = 0.014
Let wB = x g, wA = 100 g
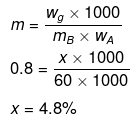
Example 34. A very small amount of a non-volatile solute (that does not dissociate) is dissolved in 56.8 cm3 of benzene (density 0.889 g cm-3). At room temperature, vapour pressure of this solution is 98.8 mm Hg while that of benzene is 100 mm Hg. Find the molality of the solution. If the freezing temperature of this solution is 0.73 degree lower than that of benzene, what is the value of molal freezing point depression constant of benzene?
Solution.
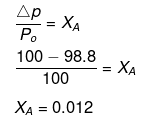
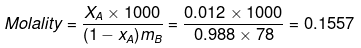
ΔTf = Kf × Molality
0.73 = Kf × 0.1557
Kf = 4.688
Example 35. x g of a non-electrolytic compound (molar mass = 200) is dissolved in 1.0 litre of 0.05 M NaCl solution. The osmotic pressure of this solution is found to be 4.92 atm at 27ºC. Calculate the value of `x'. Assume complete dissociation of NaCl and ideal behaviour of this solution.
(a) 16.52 gm
(b) 24.032 gm
(c) 19.959 gm
(d) 12.35 gm
Ans. (c)
Solution.
(i) For NaCl : p = iCRT = 2 × 0.05 × 0.0821 × 300 = 2.463 atm
(ii) For unknown compound,

Total osmotic pressure p = p1 + p2
4.92 = 2.463 + 0.1231 x
x = 19.959 g
Example 36. The freezing point of a solution containing 50 cm3 of ethylene glycol in 50 g of water is found to be -34ºC. Assuming ideal behaviour, calculate the density of ethylene glycol (Kf for water = 1.86 K kg mol-1).
(a) 1.13 g/cm3
(b) 2.00 g/cm3
(c) 1.8 g/cm3
(d) 2.25 g/cm3
Ans. (a)
Solution.
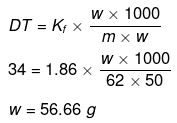
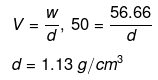
Example 37. Match the boiling point with Kb for x, y and z if molecular weight of x, y and z are same.
b. pt | Kb | |
x | 100 | 0.68 |
y | 27 | 0.53 |
z | 253 | 0.98 |
Solution. Molal elevation constant may be calculated as,
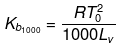
(where, Tºb = boiling point of pure solvent Lv = latent heat of vaporization.)
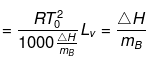
(here, ΔHV = molar latent heat of vaporization).
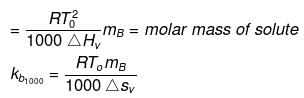
here, ΔSV = entropy of vaprization.
By considering ΔSV as almost constant, Kb µ Tº.
Kb(x) = 0.68 ; Kb (y) = 0.53 and Kb (z) = 0.98.
Example 38. 1.22 g C6H5COOH is added into two solvents and data of ΔTb and Kb are given as -
(a) ln 100 g CH3COCH3; ΔTb= 0.17; Kb = 1.7 kg kelvin/mol
(b) ln 100 g benzene; ΔTb = 0.13; Kb = 2.6 kg kelvin/mol
Find out the molecular weight of C6H5COOH in both cases and inerpret the result.
Solution.
(a)
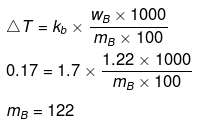
(b)
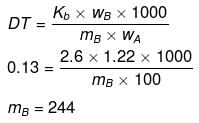
(Abnormally double molecular mass of benzoic acid, it shows association of benzoic acid in benzene).
Example 39. How much C2H5OH should be added to 1 litre H2O so that it will not freeze at -20ºC?
Kf = 1.86ºC/m
Solution. Mass of 1 litre water = 1000 g
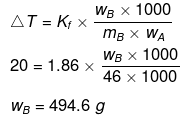
Example 40. Calculate the molarity of each of the ions in solution when 3.0 litre of 4.0 M NaCl and 4.0 litre of 2.0 M CoCl2 are mixed and diluted to 10 litre.
Solution. Molarity Na = 1.2 M
Molarity Co2+ = 0.8 M
Molarity Cl- = 2.8 M
Total Cl- ions = 28 mole.
Example 41. Calculate the molarity of each ion in solution after 2.0 litre of 3.0 M AgNO3 is mixed with 3.0 litre of 1.0 M BaCl2.
Solution.
BaCl2+ 2AgNO3 → 2AgCl +Ba(NO3)2
Initial 3 6 -_
mole
Final - -6 (ppt) 3
mole
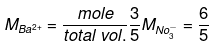
Example 42. 1.2 kg ethylene glycol was added in a car radiator containing 9 litre water. The freezing of water was just prevented when car was running in the Himalayan valley at temperature -4ºC. Sudden thunderstorm in the valley lowered the temperature to -6ºC. Calculate the amount of ice separated.
Solution.
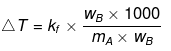
A → Solute; B → Solvent
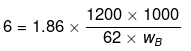
wB = 6000 g
weight of ice = (Total weight of H2O) - (wt. of H2O at 6°C) = 9000 - 6000 = 3000 g = 3 kg
Example 43. The vapour pressure of a solvent decreased by 10 mm of mercury when a non-volatile solute was added to the solvent. The mole fraction of the solute in the solution is 0.2. What should be the mole fraction of the solvent, if the decrease in the vapour pressure is to be 20 mm of mercury.
(a) 0.8
(b) 0.6
(c) 0.4
(d) 0.2
Ans. (b)
Solution.
Mole fraction of solute
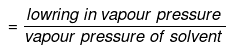
Comparing under the two conditions,
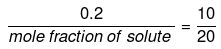
or mole fraction of solute = 0.4
mole fraction of solvent = (1 -0.4) = 0.6
Example 44. Three solutions of HCl having normality 12 N, 6 N and 2 N are mixed to obtain a solutions of 4 N normality. Which among the following volume ratio is correct for the above three components?
(a) 1 : 1 : 5
(b) 1 : 2 : 6
(c) 2 : 1 : 9
(d) 1 : 2 : 4
Ans. (b)
Solution.
Use Hit & Trial Method.
N1V1 + N2V2 + N3V3 = NR(V1 + V2 + V3)
12 × 1 6 × 2 2 × 6 = NR(9)
NR = 4
Example 45. Two solutions of H2SO4 of molarities x and y are mixed in the ratio of V1 mL : V2 mL to form a solution of molarity M1. If they are mixed in the ratio of V2mL : V1mL, they form a solution of molarity M2. Given V1. Given V1/V2 => 1 and =
, then x : y is -
(a) 2 : 1
(b) 4 : 1
(c) 1 : 2
(d) 3 : 1
Ans. (a)
Solution.
Molarity of the mixture can be calculated as.
M1V1 + M2V2 = MR(V1 + V2)
where, MR = resultant solution
(V1 × x) × (V2 × y) = M1(V1 + V2)
(V2 × x) × (V1 × y) = M2(V1 + V2)
Dividing equation (i) by equation (ii), we get
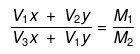
Substituting 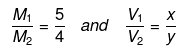 we can calculate x : y.
we can calculate x : y.
Example 46. Isuling (C2H10O5)n is dissolved in a suitable solvent and the osmotic pressure (p) of solutions of various concentrations (g/cc) C is measured at 20ºc. The slope of the plot of p against 'C' is found to be 4.65 × 10-3. The molecular weight of insulin is -
(a) 4.8 × 105
(b) 9 × 105
(c) 3 × 105
(d) 5.17 × 106
Ans. (d)
Solution.
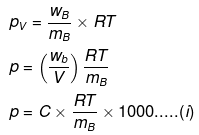
where C = concentration in g/cc,
Comparing eqs. (i) and (ii), ...(ii)

Example 47. Compound PdCl4.6H2O is a hydrated complex; 1 molal aqueous solution of it has freezing point 269.28 K. Assuming 100% ionization of complex, calculate the molecular formula of the complex (Kf for water = 1.86 K kg mol-1)
(a) [Pd(H2O)6]Cl4
(b) [Pd(H2O)4Cl2]Cl 2.2H2O
(c) [Pd(H2O)3Cl3]Cl.3H 2O
(d) [Pd(H2O)2Cl4].4H 2O
Ans. (c)
Solution.
ΔT = i × Kf × m
(273 -269.28) = i × 1.86 × 1
3.72 = i × 1.86
i = 2
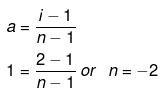
Thus, the complex should give two ions in the solution, i.e., the complex will be [Pd(H2O)3Cl3]Cl.3H2O]
Example 48. pH of 0.1 M monobasic acid is measured to be 2. Its osmotic pressure at a given temperature T K is -
(a) 0.1 RT
(b) 0.11 RT
(c) 1.1 RT
(d) 0.01 RT
Ans. (b)
Solution.
HA H+ A-
t = 0 C 0 0
teq C -C∝ C∝ C∝
[H ] = Ca, [H ] = 10-pH
Cα = 10-2
0.1 α = 10-2
a = 0.1
a = ; 0.1 =
i = 1.1
p = iCRT
= 1.1 × 0.1 × RT = 0.11 RT
Example 49. Lowering of vapour pressure in 1 molal aqueous solution at 100ºC is -
(a) 13.44 mm Hg
(b) 14.12 mm Hg
(c) 31.2 mm Hg
(d) 35.2 mm Hg
Ans. (a)
Solution.
Molality and mole fraction are related as follows:
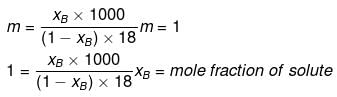
mA = molar mass of solvent
xB = 0.0176, xA = 0.9824
p = p°AxA
p = 760 × 0.9824 = 746.624
Δp = p°A - p = 760 - 746.624 = 13.4 mm Hg.
Example 50. Calculate normality of the mixture obtained by mixing 100ml of 0.1N HCl and 50ml of 0.25N NaOH solution.
(a) 0.0467 N
(b) 0.0367 N
(c) 0.0267 N
(d) 0.0167 N
Ans. (d)
Solution.
Molal eq. of HCl = 100 × 0.1 = 10
Molal eq. of NaOH = 50 × 0.25 = 12.5
HCl and NaOH neutralize each other with equal eq.
Eq. of NaOH left = 12.5 - 10 = 2.5
Volume of new solution = 100 + 50 = 150 ml.
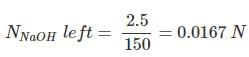
Hence normality of the mixture obtained is 0.0167 N
Example 51. 300 ml 0.1 M HCl and 200 ml of 0.03M H2SO4 are mixed. Calculate the normality of the resulting mixture-
(a) 0.084 N
(b) 0.84 N
(c) 2.04 N
(d) 2.84 N
Ans. (a)
Solution.
For HCl For H2SO4
V1 = 300 ml V2 = 200 ml
N1 = M × Basicity N2 = M × Basicity
= 0.1 × 1 = 0.1 = 0.03 × 2 = 0.06
Normality of the mixture
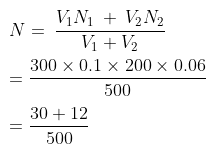
= 0.084 N
Example 52. In what ratio should a 6.5 N HNO3 be diluted with water to get 3.5 N HNO3?
(a) 6 : 7
(b) 7 : 6
(c) 5 : 6
(d) 6 : 5
Ans. (b)
Solution.
N1V1 = N2V2
6.5 V1 = 3.5 (V1 x)
6.5 V1 = 3.5 V1 3.5 x
3 V1 = 3.5 x
Example 53. Calculate the amount of each in the following solutions -
(i) 150 ml of N/7 H2SO4
(ii) 250 ml of 0.2M NaHCO3
(iii) 400 ml of N/10 Na2CO3
(iv) 1052 g of 1 m KOH.
(a) 52g, 2.12g, 4.2g, 1.05g
(b) 1.05g, 4.2g, 2.12g, 52g
(c) 1.05g, 2.12g, 52g, 4.2g
(d) 4.2g, 2.12g, 1.05g, 52g
Ans. (b)
Solution.
(i) Eq. wt. of H2SO4
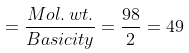
Amount of H2SO4 per litre (strength) = Normality × Eq. wt. = × 49 = 7 g/litre
Amount in 150 ml 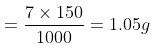
(ii) Molecular wt. of
NaHCO3 = 23 1 12 48 = 84
Amount of NaHCO3 required to produce 1000 c.c. of one molar solution = 84 g
Amount present per litre in 0.2 M solution = 84 × 0.2 = 16.8 g
Amount present in 250 c.c.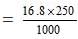
= 4.2 g
(iii) Equivalent weight of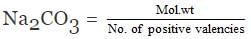
= 53
Amount of Na2CO3 = Normality × Eq. wt. = × 53 = 5.3 g/litre
Amount present in 400 c.c.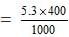
= 2.12 g
(iv) We know that 1 molal solution of a substance contains 1000 g of solvent.
Wt. of KOH in 1052 g of 1 m KOH solution = 1052 - 1000 = 52 g
Example 54. How many kilograms of wet NaOH containing 12% water are required to prepare 60 litres of 0.50 N solution ?
(a) 1.36 kg
(b) 1.50 kg
(c) 2.40 gm
(d) 3.16 kg
Ans. (a)
Solution.
One litre of 0.50 N NaOH contains = 0.50 × 40g = 20 g = 0.020 kg
60 litres of 0.50 N NaOH contain
= 0.020 × 60 kg = 1.20 kg NaOH
Since the given NaOH contains 12% water, the amount of pure NaOH in 100 kg of the given NaOH = 100 - 12 = 88 kg
Thus 88 kg of pure NaOH is present in 100 kg wet NaOH
1.20 kg of pure NaOH is present in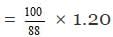
= 1.36 kg wet NaOH
Example 55. Calculate the vapour pressure of a solution at 1000C containing 3g of cane sugar in 33g of water. (At wt. C = 12 , H = 1 , O = 16)
(a) 760 mm
(b) 756.90 mm
(c) 758.30 mm
(d) None
Ans. (b)
Solution.
Vapour pressure of pure water (solvent) at 1000C, p° = 760 mm.
Vapour pressure of solution, p = ?
Wt. of solvent, W = 33g
Wt. of solute, w = 3g
Mol. wt. of water (H2O), M = 18
Mol. wt. of sugar (C12H22O11),
m = (12 × 12) + (22 × 1) + (11 × 16) = 342
According to Raoult's law,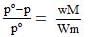
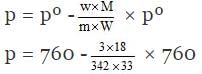
(pº for H2O = 760 mm)
= 760 - 3.19 = 756.90 mm
Example 56. Osmotic pressure of a sugar solution at 24°C is 2.5 atmospheres. Determine the concentration of the solution in gm mole per litre.
(a) 0.0821 moles/litre
(b) 1.082 moles/litre
(c) 0.1025 moles/litre
(d) 0.0827 moles/litre
Ans. (c)
Solution.
Here it is given that
p = 2.5 atm, T = 24 273 = 297K, S = 0.0821 lit. atm. deg-1 mol-1, C = ?
We know that p = CST
or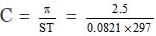
= 0.1025 moles/litre
Example 57. Twenty grams of a substance were dissolved in 500 ml. of water and the osmotic pressure of the solution was found to be 600 mm of mercury at 15ºC. Determine the molecular weight of the substance-
(a) 1120
(b) 1198
(c) 1200
(d) None of these
Ans. (c)
Solution.
Here it is given that
w = 20 gm ; V = 500 ml.
= 500/1000 = 0.5 litre
p = 600 mm = 600/760 atm;
T = 15 273 = 2880A
m = ?
According to Van't Hoff equation,
pV = nST pV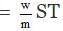
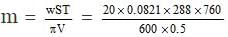
= 1198
Example 58. Blood plasma has the following composition (milli-equivalents per litre). Calculate its osmotic pressure at 370C.
Na = 138 , Ca2 = 5.2, K = 4.5, Mg2 = 2.0 , Cl¯ = 105, HCO3¯ = 25, PO43-= 2.2 , SO42-= 0.5,
Proteins = 16, Others = 1.0
(a) 7.47 atm
(b) 7.30 atm
(c) 7.29 atm
(d) 7.40 atm
Ans. (a)
Solution.
Since for calculating osmotic pressure we require millimoles/litre therefore
Na+= 138 Ca2+ = 5.2/2 = 2.6, K = 4.5,
Mg2+ = 2.0/2 = 1.0 , Cl¯ = 105,
HCO3¯ = 24,PO43-= 2.2/3 = 0.73,
SO42-= 0.5/2 = 0.25 , Proteins = 16,
others = 1.0
Total = 294.18 millimoles/litre = 294.18/1000
= 0.294 moles/litre
Now since p = CST
= 0.294 × 0.0821 × .310 = 7.47 atm
Example 59. 0.15g of a substance dissolved in 15g of solvent boiled at a temperature higher by 0.2160C than that of the pure solvent. Calculate the molecular weight of the substance. Molal elevation constant for the solvent is 2.160C.
(a) 216
(b) 100
(c) 178
(d) None of these
Ans. (b)
Solution.
Here it is given that
w = 0.15 g, DTb = 0.2160C
W = 15g Kb = 2.160C
m = ?
Substituting values in the expression,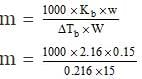
= 100
Example 60. A solution of 0.450 gm of urea (mol. wt 60) in 22.5 g of water showed 0.1700C of elevation in boiling point. Calculate the molal elevation constant of water-
(a) 0.17ºC
(b) 0.45ºC
(c) 0.51ºC
(d) 0.30ºC
Ans. (c)
Solution. Fig: Structure of urea
Fig: Structure of urea
Wt. of solute, w = 0.450 g
Wt. of solvent, W = 22.5 g
Mol. wt of solute, m = 60
Molal elevation constant Kb = ?
Boiling point elevation, DTb = 0.1700C
Substituting these values in the equation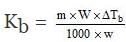
=
= 0.510C
Example 61. Calculate the boiling point of a solution containing 0.45g of camphor (mol. wt. 152) dissolved in 35.4g of acetone (b.p. 56.30C); Kb per 100 gm of acetone is 17.20C.
(a) 56.446°C
(b) 52.401°C
(c) 56.146°C
(d) 50.464°C
Ans. (a)
Solution.
Here it is given that
w = 0.45 g, W = 35.4, m = 152,
Kb = 17.2 per 100gm
Now we know that ΔTb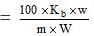
(Note that this is expression when Kb is given per 100g of the solvent)
Substituting the values in the above expression.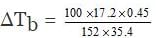
= 0.1460C
Now we know that
B.P. of solution (T) - B.P. of solvent (T0) = DT
B.P. of solution (T) = B.P. of solvent(T0) DT
Hence B.P. of solution = 56.3 0.146
= 56.4460C
Example 62. The freezing point of 0.2 molal K2SO4 is _1.1ºC. Calculate Van't Haff factor and percentage degree of dissociation of K2SO4. Kf for water is 1.86º
(a) 97.5
(b) 90.75
(c) 105.5
(d) 85.75
Ans. (a)
Solution.
ΔTf = freezing point of water -freezing point of solution = 0º C - (1.1º C) = 1.1º
We know that,
ΔTf = i × Kf × m
1.1 = i × 1.86 × 0.2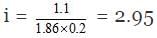
But we know
i = 1 (n - 1) a
2.95 = 1 (3 - 1) a = 1 2a
a = 0.975
Van't Haff factor (i) = 2.95
Degree of dissociation = 0.975
Percentage degree of dissociation = 97.5
|
334 videos|660 docs|300 tests
|
FAQs on Solved Examples for JEE: Solutions - Chemistry for JEE Main & Advanced
| 1. What are the eligibility criteria for the exam? |  |
| 2. How can I apply for the exam? |  |
| 3. What is the exam pattern and syllabus for the language exam? |  |
| 4. Are there any study materials or reference books available for the exam preparation? |  |
| 5. What is the passing criteria for the language exam? |  |






















