Solved Examples: States of Matter | Chemistry for JEE Main & Advanced PDF Download
Ex.1 When 2 gm of a gaseous substance A is introduced into an initially evacuated flask at 25oC, the pressure is found to be 1 atm. 3 gm another gaseous substance B is then added to it at the same temperature and pressure. The final pressure is found to be 1.5 atm. Assuming ideal gas behaviour, calculate the ratio of the molecular weights of A and B.
Sol. Let MA and MB be the molecular weights of A and B.
Using PV = nRT for A, we get :
 ...(i)
...(i)
and using Dalton's Law : PTotal =  ⇒ 1.5 =
⇒ 1.5 =  ...(ii)
...(ii)
Solving (i) and (ii), we get 
Ex.2 Which of the two gases, ammonia and hydrogen chloride, will diffuse faster and by what factor ?
Sol. By Graham's Law :
 ⇒
⇒ 
Thus, ammonia will diffuse 1.46 times faster than hydrogen chloride gas.
Ex.3 The ratio of rate of diffusion of gases A and B is 1 : 4 and their molar mass ratio is 2 : 3. Calculate the composition of the gas mixture initially effusing out.
Sol. By Graham's Law :
 ⇒
⇒  ⇒
⇒ 
⇒ Mole ratio of gas A and B effusing out =  [moles ∝ pressure]
[moles ∝ pressure]
Ex.4 At 30oC and 720 mm of Hg, the density of a gas is 1.5 g/lt. Calculate molecular mass of the gas. Also find the number of molecules in 1 cc of the gas at the same temperature.
Sol. Assuming ideal behaviour and applying ideal gas equation :
PV = nRT
Another form of gas equation is PM0 = dRT
⇒ M0 =  =
=  (T = 30 273 K)
(T = 30 273 K)
⇒ M0 = 39.38
Now number of molecules = n x N0
 = 2.29 x 1019
= 2.29 x 1019
Ex.5 The pressure exerted by 12 gm of an ideal gas at temperature toC in a vessel of volume V litre is one atm. When the temperature is increased by 10o at the same volume, the pressure rises by 10% calculate the temperature t and volume V. (molecular mass of the gas = 120 gm/mole)
Sol. Using Gas equation : PV = nRT
We have, P x V = 0.1 x R x t ...(1)
and 1.1 P x V = 0.1 x R x (t + 10) ...(2)
Using (i) and (ii), we have : 
⇒ t = 100 k or t = - 173oC
Putting the value of t in (i), we get :
⇒ 1 x V = 0.1 x 0.0821 x 100 ⇒ V = 0.821 L
Ex.6 Assuming that the air is essentially a mixture of nitrogen and oxygen in mole ratio of 4 : 1 by volume. Calculate the partial pressures of N2 and O2 on a day when the atmospheric pressure is 750 mm of Hg. Neglect the pressure of other gases.
Sol. From Dalton's Law of partial pressure, we have
Partial pressure of nitrogen =  x P and Partial pressure of oxygen =
x P and Partial pressure of oxygen = 
Now, , and
⇒  x 750 = 600 mm of Hg and
x 750 = 600 mm of Hg and  = 150 mm of Hg
= 150 mm of Hg
Ex.7 An open vessel at 27oC is heated until three fifth of the air has been expelled, Assuming that the volume of the vessel remains constant, find the temperature to which the vessel has been heated.
Sol. In the given questions, volume is constant. Also, as the vessel is open to atmosphere, the pressure is constant. This means that the gas equation is simply reduced to the following form :
nT = constant (Use PV = nRT)
or n1 T1 = n2 T2
Now let n1 = initial moles and n2 = final moles
⇒ n2 = 2/5 x n1 (as 3/5th of the air has been expelled)
⇒ T2 =  =
=  =
= 
⇒ T2 =  = 750 K = 477oC
= 750 K = 477oC
Ex.8 When 3.2 gm of sulphur is vaporized at 450oC and 723 mm pressure, the vapour occupies a volume of 780 m, what is the formula for the sulphur under these conditions ?
Sol. The molecular weight = no. of atoms x atomic mass
So let us find the molecular weight of S from the data given.

⇒ Number of atoms = 
Hence, molecular formula of sulphur = S8
Ex.9 A spherical balloon of 21 cm diameter is to be filled with H2 at NTP from a cylinder containing the gas at 20 atm at 27oC. If the cylinder can hold 2.80L of water, calculate the number of balloons that can be filled up.
Sol. The capacity of cylinder = 2.80 L
Let n = moles of hydrogen contained in cylinder and n0 = moles of hydrogen required to fill one balloon.
n = 
 (Note : the balloons are being filled at S.T.P.)
(Note : the balloons are being filled at S.T.P.)
=  =
= 
⇒ Number of balloons that can be filled = n/n0 = 10.50 ≈ 10
Ex.10 A mixture containing 1.12L of H2 and 1.12L of D2 (deuterium) at S.T.P. is taken inside a bulb connected to another bulb by a stop-cock with a small opening. The second bulb is fully evacuated; the stop-cock is opened for a certain time and then closed. The first bulb is found to contain 0.05 gm of H2. Determine the % age composition by weight of the gases in the second bulb.
Sol. In the first bulb :
Initial moles of H2 = 1.12 / 22.4 = 1/20
Initial moles of D2 = 1.12/22.4 = 1/20
Now after opening of stop-cock, mass of H2 left in the first bulb = 0.05
⇒ Moles of H2 = 0.05/2 = 1/40
⇒ Moles of H2 effused into second bulb = 1/20 - 1/40 = 1/40
Let n be number of moles of D2 effused.
From Graham's Law :
⇒  = moles of D2 in second bulb.
= moles of D2 in second bulb.
In the second bulb :
The mass of H2 gas = 1/40 x 2 = 0.05 gm
The mass of D2 gas = √2/80 x 4 = 0.07 gm
⇒ Total mass = 0.05 0.07 = 0.12 gm
⇒ % of H2 = 0.05/1.12 x 100 = 41.67 %
⇒ % of D2 = 0.07/1.12 x 100 = 58.13 %
Ex.11 The pressure in a bulb dropped from 2000 mm to 1500 mm of Hg in 47 min when the contained O2 leaked through a small hole. The bulb was then completely evacuated. A mixture of oxygen and another gas (B) of molecular weight 79 in the molar ratio of 1 : 1 at a total pressure of 4000 mm of Hg was introduced. Find the molar ratio of the two gases remaining in the bulb after a period of 74 min.
Sol. Now as P ∝ n (moles), we define the rate of diffusion as the drop in the pressure per second. First we try to find the rate of diffusion of the gas B.
The rate of diffusion of O2 = R0 = (2000 - 1500)/47 = 10.638 mm/min.
Assuming that gas B was present alone in the bulb. Let the rate of diffusion of B = RB.
From Graham's Law of diffusion, we have :


Now the bulb contains mixture of O2 and B in the mole ration of 1 : 1 at total pressure of 4000 mm Hg.
 of Hg
of Hg
As the pressure and temperature conditions are same for both gases in the second case (same bulb), so the rate of diffusion will remain same in the second case also.
Let X0 and XB be the final pressure in the bulb after leakage for 74 minutes.



As P x n
⇒ Ratio of moles is given as : XO : XB = 1 : 1235
Ex.12 A 672 ml of a mixture of oxygen-ozone at N.T.P. were found to be weigh 1 gm. Calculate the volume of ozone in the mixture.
Sol. Let V ml of ozone are there in the mixture
⇒ (672 - V) m; = vol. of oxygen
Mass of ozone at N.T.P. = 
Mass of oxygen at N.T.P. 

Ex.13 A 20 L flask contains 4.0 gm of O2 & 0.6 gm of H2 at 100oC. If the contents are allowed to react to form water vapors at 100oC, find the contents of flask and there partial pressures.
Sol. H2 reacts with O2 to form water [H2O(g)]

⇒ 2 moles of H2 = 1 mole of O2 = 2 moles of H2O
Here masses of H2 and O2 are given, so one of them can be in excess. So first check out which of the reactants is in excess.
Now, Moles of O2 = 4/32 = 0.125 and Moles of H2 = 0.6/2 = 0.3
Since 1 mole of O2 ≡ 2 moles of H2
⇒ 0.125 moles of O2 ≡ 2 x 0.125 moles of H2
i.e. 0.25 moles of H2 are used, so O2 reacts completely whereas H2 is in excess.
⇒ Moles of H2 in excess = 0.3 - 0.25 = 0.05 moles.
Also, 2 moles of H2 ≡ 2 moles of H2O
⇒ 0.25 moles of H2 ≡ 0.25 moles of H2O are produced.
⇒ Total moles after the reaction = 0.05 (moles of H2) 0.25 (moles of H2O) = 0.3
⇒ The total pressure PTotal at the end of reaction is given by :

Now partial pressure of A = mole fraction of A x PTotal
Ex.14 The compressibility factor for 1 mole of a van Waals gas at 0oC and 100 atm pressure is found to be 0.5. Assuming that the volume of gas molecular is negligible, calculate the van der Waals constant `a'.
Using van der Waal's equation of state :

Now : V - nb  V(given)
V(given)
⇒ The equation is reduced to : 
or 


Also, 
Substitute the values of V and T :
⇒ a = 1.25 litre2 mol-2 atm.
Ex.15 Calculate the pressure exerted by 5 mole of CO2 in one litre vessel at 47oC using van der waals equation. Also report the pressure of gas if it behaves ideally in nature. (a = 3.592 atm litre2 mol-2, b = 0.0427 litre mol-1)
Using van der waals equation of state :

Substituting the given values, we get :

If the gas behaves ideally, then using : PV = nRT

Solved Examples
IIT-JEE MAINS
Ex.1 A gas occupies 300 ml at 27oC and 730 mm pressure. What would be its volume at STP-
(A) 162.2 ml (B) 262.2 ml (C) 362.2 ml (D) 462.2 ml
Sol. (B)
Given at T1 = 300 K, T2 = 273 K (STP)
V1 = 300 ml =  litre, P1 =
litre, P1 =  atm. P2 = 1 atm., V2 = ?
atm. P2 = 1 atm., V2 = ?
Q  =
=  ,
,
 =
= 
V2 = 0.2622 litre = 262.2 ml.
Ex.2 A truck carrying oxygen cylinders is filled with oxygen at -23oC and at a pressure of 3 atmosphere in Srinagar, Kashmir. Determine the internal pressure when the truck drives through Madras, Tamil Nadu. Where the temperature is 30oC -
(A) 2.64 atm. (B) 1.64 atm. (C) 1 atm. (D) 3.64 atm.
Sol. (D)
P1 = 3 atm., P2 = ?
T1 = - 23 + 273 = 250 K
T2 = 273 + 30 = 303 K.
 =
=  ,
,
 =
= 
P2 =  = 3.64 atm.
= 3.64 atm.
Ex.3 The density of a gas at -23oC and 780 torr is 1.40 gram per litre. Which one of the following gases is it -
(A) CO2 (B) SO2 (C) Cl2 (D) N2
Sol. (D)
PV = nRT
 x 1 = n x .082 x (273 - 23)
x 1 = n x .082 x (273 - 23)
n = 
n = 0.0501 moles.
Q .0501 moles of the gas weigh = 1.40 gm.
1 mole of gas weigh =  = 28 gram.
= 28 gram.
So gas is N2.
Ex. 4 Calculate the weight of CH4 in a 9 litre cylinder at 16 atm and 27oC (R = 0.08 lit. atm/k) -
(A) 96 gm (B) 86 gm (C) 80 gm (D) 90 gm
Sol. (A)
Given P = 16 atm, V = 9 litre.
T = 300 K, mCH4 = 16, R = 0.08 litre atm/k.
PV = w/m x R x T
16 x 9 =  x 0.08 x 300
x 0.08 x 300
w = 96 gm.
Ex. 5 What is the density of sulphur dioxide (SO2) at STP -
(A) 2.86 gm/lit. (B) 1.76 gm/lit (C) 1.86 gm/lit (D) None of these.
Sol. (A)
The gram molecular weight of SO2 = 64 gm/mole.
Since 1 mole of SO2 occupies a volume of 22.4 litres at S.T.P.
Density of SO2 = = 2.86 gm/lit.
= 2.86 gm/lit.
Ex.6 5gm of XeF4 gas was introduced into a vessel of 6 litre capacity at 80oC. What is the pressure of the gas in atmosphere -
(A) .21 atm (B) .31 atm (C) .11 atm (D) .41 atm.
Sol. (C)
Given V = 6 litre, T = 353 K, R= 0.082, W = 5gm. m= 207.3
PV =  x R x T
x R x T
P x 6 =  x 0.082 x (273 80)
x 0.082 x (273 80)
P =  = .11 atm.
= .11 atm.
Ex.7 Calculate the temperature at which 28 gm N2 occupies a volume of 10 litre at 2.46 atm-
(A) 300 K (B) 320 K (C) 340 K (D) 280 K
Sol. (A)
Given wN2 = 28gm ,
P = 2.46 atm, V = 10 litre. mN2 = 28,
Q PV =  RT
RT
2.46 x 10 =  x 0.0821 x T
x 0.0821 x T
T = 300 K.
Ex.8 A mixture of gases at 760 mm pressure contains 65% nitrogen, 15% oxygen and 20% Carbon dioxide by volume. What is the partial pressure of each in mm -
(A) 494, 114, 252 (B) 494, 224, 152
(C) 494, 114, 152 (D) None of these.
Sol. (C)
P'N2 = 760 x  = 494 mm
= 494 mm
P'O2 = 760 x  = 114 mm
= 114 mm
P'CO2 = 760 x  = 152 mm.
= 152 mm.
Ex.9 0.45 gm of a gas 1 of molecular weight 60 and 0.22 gm of a gas 2 of molecular weight 44 exert a total pressure of 75 cm of mercury. Calculate the partial pressure of the gas 2 -
(A) 30 cm of Hg (B) 20 cm of Hg (C) 10 cm of Hg (D) 40 cm of Hg.
Sol. (A)
No. of moles of gas 1 = n1 = = 
= 0.0075
No. of moles of gas 2 = n2 =  =
= 
= 0.0050
Total no. of moles = n1 n2
= 0.0075 0.0050 = 0.0125
P2 partial pressure of gas 2 =  x 75 = 30 cm of Hg.
x 75 = 30 cm of Hg.
Ex. 10 The total pressure of a sample of methane collected over water is 735 torr at 29oC. The aqueous tension at 29oC is 30 torr. What is the pressure exerted by dry methane -
(A) 605 torr (B) 205 torr (C) 405 torr (D) 705 torr
Sol. (D)
Ptotal = Pdry methane Pwater
735 = Pdry methane 30
Pdry methane = 735 - 30 = 705 torr.
Ex.11 The odour from a gas A takes six seconds to reach a wall from a given point. If the molecular weight of gas A is 46 grams per mole and the molecular weight of gas B is 64 grams per mole. How long will it take for the odour from gas B to reach the same wall from the same point. Approximately -
(A) 6 Sec (B) 7 Sec (C) 8 Sec (D) 9 Sec
Sol. (B)
 =
= 
 =
=  = 1.18
= 1.18
Time taken for the odour of B to reach the wall = 1.18 x 6 = 7.08 sec  7 sec.
7 sec.
Ex.12 1 litre of oxygen effuses through a small hole in 60 min. and a litre of helium at the same temperature and pressure effuses through the same hole in 21.2 min. What is the atomic weight of Helium -
(A) 2.99 (B) 3.99 (C) 2.08 (D) 1.99
Sol. (B)
 =
=  =
=  =
= 
= 
Squaring both of sides =  =
=  MHe =
MHe =  = 3.99
= 3.99
Since Helium is monoatomic so
Atomic weight = Molecular weight = 3.99
Ex.13 What is the temperature at which oxygen molecules have the same r.m.s. velocity as the hydrogen molecules at 27oC -
(A) 3527oC (B) 4227oC (C) 4527oC (D) 4000oC
Sol. (C)
r.m.s. velocity C = 
For oxygen Co2 = 
For CH2 at 27oC = 
When Co2 = CH2
 =
= 

T =  = 4800 K.
= 4800 K.
Then in oC T = 4800 - 273 = 4527oC
Ex.14 Calculate the total kinetic energy in joules, of the molecules in 8 gm of methane at 27oC -
(A) 1770.5 Joule (B) 1870.5 joule (C) 1970.5 joule (D) 1670.5 joule
Sol. (B)
EK (For 1 mole) = RT = 3741 Joule.
Total energy of 8 gm of methane
= 1/2 mole of methane
=  = 1870.5 Joule.
= 1870.5 Joule.
Ex.15 Calculate the root mean square velocity of SO2 at S.T.P. -
(A) 3.26 x 104 cm/sec (B) 1.26 x 102 cm/sec
(C) 1.26 x 104 cm/sec (D) 3.26 x 102 cm/sec
Sol. (A)
vrms of SO2 =
=  = 3.26 x 104 cm/sec.
= 3.26 x 104 cm/sec.
Ex.16 Calculate the number of atoms in 1 g of helium
(A) 1.506 x 1023 atoms (B) 1.605 x 1032 atoms (C) 1.056 x 1025 atoms (D) None of these
Sol. (A)
Atomic mass of He = 4
4 g of He contain = 6.023 x 1023 atoms
1 g of He contains =
 = 1.506 x 1023 atoms.
= 1.506 x 1023 atoms.
Ex.17 7.00 g of a gas occupies a volume of 4.1 litres at 300 K and 1 atmosphere pressure. Calculate the molecular mass of the gas -
(A) 40 g mol-1 (B) 42 g mol-1 (C) 48 g mol-1 (D) 45 g mol-1
Sol. (B)
PV = nRT , n = PV/RT
n =  = mol
= mol
now n =  = =
= = 
Thus, molecular mass of gas = 7 x 6
= 42 g mol-1
Ex.18 Calculate density of ammonia at 30oC and 5 atm. pressure -
(A) 3.03 g/litres. (B) 3.82 g/litres (C) 3.42 g/litres. (D) 4.42 g/litres.
Sol. (C)
PV = nRT, or PV =  RT or P =
RT or P =  x
x  or P = d x
or P = d x 
d = MP/RT ; d =  = 3.42 g/litres.
= 3.42 g/litres.
Ex.19 3 moles of a gas are present in a vessel at a temperature of 27oC . Calculate the value of gas constant (R) in terms of kinetic energy of the molecules of gas -
(A) 7.4 x 10-4 KE per degree kelvin.
(B) 4.5 x 10-4 KE per degree kelvin.
(C) 7.4 x 10-5 KE per degree kelvin.
(D) None of these
Sol. [A] K.E. for 1 mole = 3/2 RT
K.E. for 3 moles = 9/2 RT. or R =  KE =
KE = 
= 7.4 x 10-4 KE per degree kelvin.
Ex.20 In the following diagram, container of NH3 gas and container of HCl gas, connected through a long tube, are opened simultaneously at both ends; the white NH4Cl ring first formed will be at Q point. If OP = 40cm, then find OQ -

(A) 35 cm (B) 23.74 cm (C) 30 cm (D) 31.25 cm
Sol. [B]
Let OQ = x cm so QP = (40 - x) cm
Diffused volume of NH3 gas = Area of T.S. of tube x Distance travelled by NH3 gas
 = A x OQ = Ax
= A x OQ = Ax
{Where A is area of T.S. of tube}
Similarly in the same time,
Diffused volume of HCl gas = Area of T.S. of tube x Distance travelled by HCl gas
VHCl = A x QP = A (40 - x)
From Graham's Law of diffusion
⇒  =
= 
⇒  =
=  = 1.46
= 1.46
⇒  = 1.46
= 1.46
⇒ x = 23.74 cm
OQ = 23.74 cm
Ex.21 The root mean square velocity of hydrogen is times than that of nitrogen. If T is the temperature of the gas, then :
(A)  =
=  (B)
(B)  >
>  (C)
(C)  <
<  (D)
(D)  =
= 
Sol. [C] Vrms =  =
=  =
=  ;
;
=
 x
x  =
= 
=  =
= 
= 5 =  x 14
x 14
 x 5 =
x 5 =  x 14
x 14
 >
> 
Ex.22 A jar contains a gas and a few drops of water. The pressure in the jar is 830 mm of Hg. The temperature of the jar is reduced by 1% . The vapour pressure of water at two temperature are 30 and 25 mm of Hg. Calculate the new pressure in jar.
(A) 792 mm of Hg (B) 817 mm of Hg (C) 800 mm of Hg (D) 840 mm of Hg
Sol. [B] Pgas = Pdry gas Pmoisture at T K
or Pdry = 830 - 30 = 800
Now at T2 = 0.99 T1 ;
at constant volume = 
Pdry =  = 792 mm
= 792 mm
Pgas = Pdry Pmoisture
= 792 25 = 817 mm
Ex.23 Calculate relative rate of effusion of O2 to CH4 through a container containing O2 and CH4 in 3 : 2 mass ratio.
(A)  (B)
(B)  (C)
(C)  (D) None of these
(D) None of these
Sol. [B] =
=  =
= 
=  x
x  x
x  =
= 
Ex.24 At what temperature will average speed of the molecule of the second member of the series CnH2n be the same of Cl2 at 627oC ?
(A) 259.4 K (B) 400 K (C) 532.4 K (D) None of these
Sol. [C] Second member of CnH2n series =C3H6 = 42
=  =
=  =
=  =
= 
T2 = 532.4 K
Ex.25 80 mL of O2 takes 2 minute to pass through the hole. What volume of SO2 will pass through the hole in 3 minute ?
(A)  (B) 120 x
(B) 120 x  (C)
(C)  (D) None of these
(D) None of these
Sol. [A] =
=  =
=  =
=  ;
;
 =
=  =
= ; V2 =
; V2 = 
Ex.26 The density of a gas filled electric lamp is 0.75 kg/m3. After the lamp has been switched on, the pressure in it increases from 4 x 104 Pa to 9 x 104 pa. What is increases in URMS ?
(A) 100 (B) 200 (C) 300 (D) None of these
Sol. [B] U1 = 
DUrms =  (
( -
-  )
)
=  (300 - 200)
(300 - 200)
=  x 100 = 200
x 100 = 200
Ex.27 If one mole each of a monoatomic and diatomic gases are mixed at low temperature then CP/CV ratio for the mixture is :
(A) 1.40 (B) 1.428 (C) 1.5 (D) 1.33
Sol. [C] Cv =  = 2R
= 2R
Cp =  = 3R
= 3R
 = 1.5
= 1.5
Ex.28 If one mole of a monatomic gas (g = 5/3) is mixed with one mole of a diatomic gas (g = 7/5), the value of g for the mixture is :
(A) 1.4 (B) 1.5 (C) 1.53 (D) 3.07
Sol. [B]

Thus, for mixture of 1 mole each,
Cv =  and Cp =
and Cp = 
Thus,  =
=  = 1.5
= 1.5
Ex.29 The average speed at temperature ToC of CH4(g) is  x 103 ms-1. What is the value of T ?
x 103 ms-1. What is the value of T ?
(A) 240.55oC (B) -32.45oC (C) 3000oC (D) -24.055oC
Sol. [B] =
=  =
= 
 =
=  x 106
x 106
T =  = 240.55 K
= 240.55 K
ToC = 240.55 - 273 = -32.45oC
Ex.30 The intercept on y-axis and slope of curve plotted between P/T vs T
For an ideal gas having 10 moles in a closed rigid container of volume 821. L. (P = pressure in atm and T = Temp. in K , log10 2 = 0.30) are respectively
(A) 0.01, 0 (B) 0.1, 1 (C) 0.1,0 (D) 10,1
Sol. [B] Intercept on y-axis
= log10 = log10
= log10 = -1.0
= -1.0
 v/s curve
v/s curve  =
= 
Intercept =  =
=  = 0.1, slope = 0
= 0.1, slope = 0
Ex.31 Two vessels connected by a valve of negligible volume. One container (I) has 2.8 g of N2 at temperature T1 (K) The other container (II) is completely evacuated. The container (I) is heated to T2 (K) while container (II) is maintained at T2/3(K). volume of vessel (I) is half that of vessel (II). If the valve is opened then what is the weight ratio of N2 in both vessel (WI/WII) ?
(A) 1 : 2 (B) 1 : 3 (C) 1 : 6 (D) 3 : 1
Sol. [C] 
Let x mole of N2 present into vessel II and P is final pressure of N2
P(2V) = xR(T2/3) and P (V) = (0.1 - x) RT2
⇒ 2 = 
⇒ x = 0.6/7 mole
 x 28 ⇒ 2.4 g N2
x 28 ⇒ 2.4 g N2
II has 2.4 g N2 and I has 0.4 g of N2;
 =
=  ⇒ 1 : 6
⇒ 1 : 6
Ex.32 7 moles of a tetra-atomic non-linear gas `A' at 10 atm and T K are mixed with 6 moles of another gas B at K and 5 atm in a closed, rigid vessel without energy transfer with surroundings. If final temperature of mixture was  K, then gas B is ? (Assuming all modes of energy are active)
K, then gas B is ? (Assuming all modes of energy are active)
Sol. 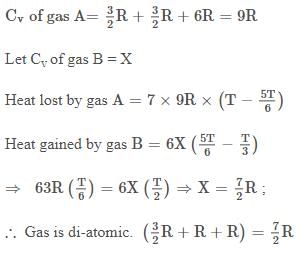
|
352 videos|596 docs|309 tests
|
|
352 videos|596 docs|309 tests
|

|
Explore Courses for JEE exam
|

|


















