Solved Examples for JEE: Thermodynamics | Chemistry for JEE Main & Advanced PDF Download
Example 1. Show that pressure of a fixed amount of an ideal gas is a state function 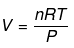
Solution.

 =
= 

Example 2. Calculate work done for the expansion of a substance 3m3 to 5m3 against.
(a) Constant pressure = 105 Pa
(b) A veriable pressure = (10 + 5V) Pa
Solution.
(a) W = -PdV = -105(5-3) = -2 ×105 J
(b)
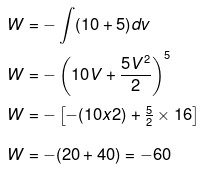
Example 3. Calculate change in internal energy for a gas under going from state-I
(300 K, 2 ×10-2 m3) to state -II (400 K, 4 ×10-2 m3) for one mol. of vanderwaal gas.
(a) If gas is ideal [Cv = 12 J/K/mol]
(b) If gas is real

Cv = 12 J/k/ mol
a = 2 J.m./mol2
Solution.
(a) DU = nCV(T2 - T1)
= 1 × 12 ×100 = 1200 J
(b)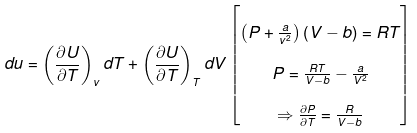
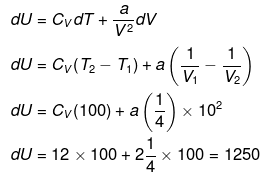
Example 4. One mole of an ideal gas is expanded isothermally at 300 K from 10 atm to 1 atm. Calculate q, w, DU & DH under the following conditions.
(i) Expansion is carried out reversibly.
(ii) Expansion is carried out irreversibly
Solution.
Isothermal process
(i) For ideal gas ΔU = 0, ΔH = 0
q = - w
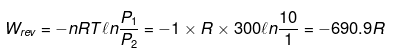
(ii)
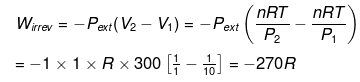
Example 5. Calculate work done for an ideal gas (ln 2 = 0.7)
 Solution.
Solution.
w = -nRT ln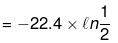
= 22.4 × 0.7 = 15.68
Example 6. Calculate w = ? (ln 2 = 0.7)
 Solution.
Solution.
P - V Relation from plot
y = mx + C
1 = m + C .............(1)
4 = 2m + C .............(2)
⇒ m = 3, C = -2
Hence,


Example 7. One mole an ideal gas is expanded from (10 atm, 10 lit) to (2 atm, 50 litre) isothermally. First against 5 atm then against 2 atm. Calculate work done in each step and compare it with single step work done with 2 atm.
Solution.
(i) P1V1 = P2V2
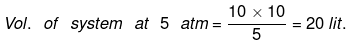 wirrev = - Pext(V2 - V1) = - 5 (20 - 10) = - 50 atm lit.
wirrev = - Pext(V2 - V1) = - 5 (20 - 10) = - 50 atm lit.
(ii) Work done against 2 atm
P1 V1 P2 V2
P2 V2
5 atm 20 lit 2 atm 50 lit
wirrev = - Pext(V2 - V1) = - 2 (50 - 20) = - 60 atm lit.
wtotal = - 50 - 60 = - 110 atm lit.
P1 V1 P2 V2
P2 V2
10 atm 10 lit 2 atm 50 lit
w = - 2 (50 - 10) = - 80 lit
magnitude of work done in more than one step is more than single step work done.
Example 8. For 1 mole of monoatomic gas. Calculate w, DU, DH, q

Solution.
Isochoric process
w = 0
q = dU = Cv (T2 - T1)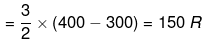
DH = CpΔT = R (400 - 300) = 250 R
Example 9. One mole of an non linear triatomic ideal gas is expanded adiabatically at 300 K from 16 atm to 1 atm.
Calculate Work done under the following conditions.
(i) Expansion is carried out reversibly.
(ii) Expansion is carried out irreversibly
Solution.
q = 0
w = DU = Cv(T2 - T1)
Cv for triatomic non linear gas = 3R
(i) For rev. process. , r = 4/3
, r = 4/3
ΔU = w = 3R (150 - 300) = - 450 R
(ii) n = 1
- Pext (V2 - V1) = Cv (T2 - T1)



-16T2 T1 = 48 T2 - 48 T1
49 T1 = 64 T2
T2 = 229.69
wirr = Cv(T2 - T1) 3R (229.69 - 300)
= - 210.93 R
Example 10. One mole of an non linear triatomic ideal gas is compressed adiabatically at 300 K from 1 atom to 16 atm.
Calculate Work done under the following conditions.
(i) Expansion is carried out reversibly. (ii) Expansion is carried out irreversibly.
Solution.
q = 0 Adiabatic process
(i)
wrev = DU = Cv(T2 - T1)


w = 3R (600 - 300) = 900 R
(ii)


- (T2 - 16 T1) = 3R (T2 - T1)
- T2 16 T1 = 3T2 - 3T1
4T2 = 19 T1
w = ΔU = 3R (1425 - 300) = 3375 R
Example 11. Calculate work done in process BC for 1 mol of an ideal gas if total 600 cal heat is released by the gas in whole process.

Solution.
For cyclic process
dU = 0
q = - w
PV1 =1× R × 300
PV2 =1× R × 400
⇒ P(V2 - V1) = R (400 - 300)
q = - (wBA + wAC + wCB)
- 600 = - (0 + (-) 2) × (400 - 300) + wCB
wCB = 800 cal
Example 12. Calculate entropy change in each step for an ideal gas (monoatomic)

Solution. 
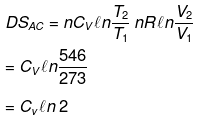
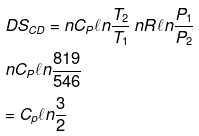
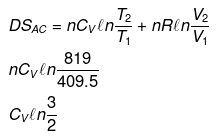
Example 13. One mole of an ideal gas is expanded isothermally at 300 K from 10 atm to 1 atm. Find the values of
ΔSsys, ΔSsurr & ΔStotal under the following conditions.
(i) Expansion is carried out reversibly.
(ii) Expansion is carried out irreversibly
(iii) Expansion is free.
Solution.
(i) 


(ii)

ΔU = 0 = q + w
qirr = pext)(v2 - v1)



(iii) Free expansion ΔT = 0
w = 0
q = 0


Example 14. One mole of an non linear triatomic ideal gas is expanded adiabatically at 300 K from 16 atm to 1 atm. Find the values of DSsys, DSsurr & DStotal under the following conditions.
(i) Expansion is carried out reversibly.
(ii) Expansion is carried out irreversibly
(iii) Expansion is free.
Solution.
For non-linear tri-atomic ideal gas
Cv = 3R, Cp = 4R
(i)
q = 0
ΔSsurr = - ΔSsys = 0
ΔStotal = 0
(ii) First of all we will have to calculate the temperature of the gas after it has undergoes the said adiabatic reversible expansion we have q = 0
ΔU = q + w
nCv (T2 - T1) = - pext (v2 - v1)
T2 = 229.68 K


= - 1.068 R + 2.77 R
= 1.702 R
ΔStotal =ΔSsys = 1.702 R
(iii) In free adiabatic expansion we have
w = 0
q = 0
ΔT = 0


Example 15. For the reaction
N2 + 2O2 → 2NO2
Given : at 1 atm, 300 K
SN2 = 180 J /mol/K Cp(N2) = 30 J/mol/K
SO2 = 220 J /mol/K Cp(O2) = 30 J/mol/K
SNO2 = 240 J /mol/K Cp(NO2) = 40 J/mol/K
Calculate
(i) ΔS300 K, 1 atm
(ii) ΔS400 K, 1 atm
(iii) ΔS300 K, 5 atm
(iv) ΔS400 K, 5 atm
Solution.
(i) (ΔSr)300 = 2SNO2 - 2SO2 - SN2
= 2 × 240 - 2 × 220 - 180
= -140 J mol-1k-1
(ΔCp)r = 2Cp(NO2)- 2Cp(O2) - Cp(N2)
= 2 × 40 - 2 × 30 - 30
= -10 J mol-1k-1
(ii) (ΔSr)400 = (ΔSr)300 (ΔCp)r ln
= - 140 - 10 ln (4/3)
= - 142.88 J mol-1k-1
(iii) (ΔSr)300k, 5 atm
= (ΔSr)300k, 1 atm ΔngRln
= - 140 (-1)Rln (1/5)
= - 140 R ln 5
=- 140 8.314 ln 5
= - 126.62 J mol-1k-1
(iv) (ΔSr)400k, 5 atm
= (ΔSr)400k, 1 atm - R ln
= 142.88 R ln 5
=-129.5 J mol-1k-1
Example 16. From the T-S diagram of a reversible carnot engine calculate:
(i) efficiency
(ii) workdone per cycle
(iii) Heat taken from the source and rejected to sink
(iv) In order to illuminate 10000 bulbs of 40 watt power each calculate the no. of cycle per second the above must go through.
Solution.
(i)
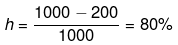
(ii) qrev1-2 = ∫Tds = 1000 x 100 J
q3-4 = ∫Tds = - 200 x 100 J
qnet = 800 × 100 = 80 kJ
W = -80 kJ
(iii) 105 J,
2 × 104 J
(iv) 5
Example 17. Calculate entropy change
H2O(l, 1 atm, 100ºC) → H2O (g, 1 atm, 110ºC)
H2O(l, 1 atm, 100ºC) → H2O (g, 2 atm, 100ºC)
ΔHvap = 40 kJ/mol Cp(l) = 75 J/mol /K Cp(g) = 35 J/mol/K
Solution.
For 1 mol
(i) H2O(l, 1 atm, 100ºC) → H2O (g, 1 atm, 100ºC) → H2O(g, 1 atm, 110ºC)
(A) (B) (C)
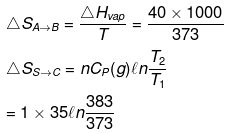
(ii) H2O(l, 1 atm, 100ºC) → H2O (g, 1 atm, 100ºC) → H2O(g, 2 atm, 100ºC)
(A) (B) (C)
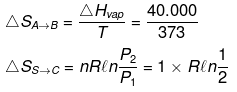
|
352 videos|596 docs|309 tests
|
FAQs on Solved Examples for JEE: Thermodynamics - Chemistry for JEE Main & Advanced
| 1. What is thermodynamics? |  |
| 2. What are the laws of thermodynamics? |  |
| 3. How do the laws of thermodynamics apply to everyday life? |  |
| 4. What is the difference between heat and temperature in thermodynamics? |  |
| 5. Can thermodynamics be applied to biological systems? |  |
|
352 videos|596 docs|309 tests
|



















