Open App

SSC CGL Exam > SSC CGL Notes > Quantitative Aptitude for SSC CGL > Solved Examples: Triangles

Solved Examples: Triangles | Quantitative Aptitude for SSC CGL PDF Download

Question 1: In a $△$ ABC, D and E are two points on sides AB and AC such that DE is parallel to BC and AD : DB = 2 : 1. If AE = 8 cm, then find the length of AC.

a) 12 cm
b) 10 cm
c) 16 cm
d) 20 cm

Solved Examples: Triangles | Quantitative Aptitude for SSC CGL

View Answer

Answer (A)

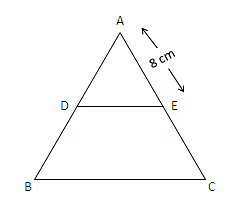
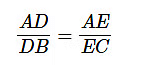
Solved Examples: Triangles | Quantitative Aptitude for SSC CGL

Here, 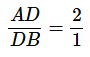Solved Examples: Triangles | Quantitative Aptitude for SSC CGL and AE = 8 cm

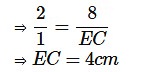
Solved Examples: Triangles | Quantitative Aptitude for SSC CGL
Here, AC = AE+EC = 4+8 = 12 cm

Question 2: In a $△$ ABC, Points D and E are on sides AB and AC such that DE is parallel to BC and AD : DB = 3 : 1 and AE = 18 cm. Then find AC.

a) 26 cm
b) 24 cm
c) 28 cm
d) 32 cm

View Answer

Answer (B)

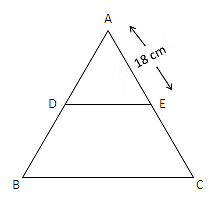
Given, DE is parallel to BC.
Then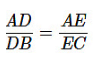

Here,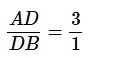
AE= 18 cm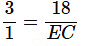
Solved Examples: Triangles | Quantitative Aptitude for SSC CGL

⇒ EC = 6 cm
AC = AE+EC = 6+18 = 24 cm

Question 3: In a $△$ ABC, points D and E are on the sides of AB and AC respectively such that DE is parallel to BC and AD : AB = 2 : 5 and AE = 4 cm. Then find AC.

a) 10 cm
b) 14 cm
c) 12 cm
d) 9 cm

View Answer

Answer (B)

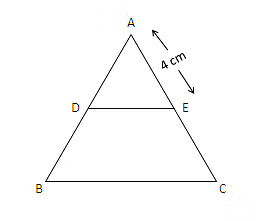
Given, DE is parallel to BC.
Then, 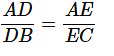Solved Examples: Triangles | Quantitative Aptitude for SSC CGL

Here,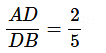 Solved Examples: Triangles | Quantitative Aptitude for SSC CGL

AE= 4 cm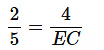
Solved Examples: Triangles | Quantitative Aptitude for SSC CGL

⇒ EC = 10 cm
AC = AE+EC = 4+10 = 14 cm

Question 4: The coordinates of the vertices of a right-angled triangle are A (6, 2), B(8, 0) and C (2, -2). The coordinates of the orthocentre of triangle PQR are

a) (2, -2)
b) (2, 1)
c) (6, 2)
d) (8, 0)

View Answer

Answer (C)
Given that the coordinates of a right-angled triangle are A (6, 2), B(8, 0) and C (2, -2).
We know that the distance between two points(a, b) &(c, d) is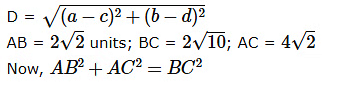
Solved Examples: Triangles | Quantitative Aptitude for SSC CGL

Therefore, angle A is right angled.
Since it is a right angled triangle, the 2 sides adjacent to the right angle will be altitudes. The third altitude must meet at the vertex at which these 2 sides meet.
Hence, the vertex that contains the right angle is the orthocentre. From the points given, we can clearly see that (6, 2) is the orthocentre. Option C is the right answer.

Question 5: find the area of an equilateral triangle if the height of the triangle is 24 cm.
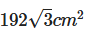
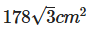
a) Solved Examples: Triangles | Quantitative Aptitude for SSC CGL
b)
c)
d)

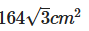
View Answer

Answer (A)
Given,
AD = 24 cm and ABC is an equilateral triangle
In an equilateral triangle all the angles are equal to 60°

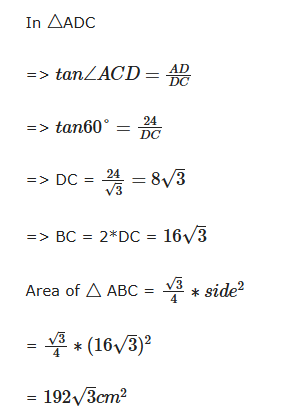
Solved Examples: Triangles | Quantitative Aptitude for SSC CGL

Question 6: Three sides of a triangular meadow are of length 28 m, 45 m and 53 m long respectively. Find the cost of sowing seeds(in rupees per sq.m) in the meadow at the rate of 12 rupees per sq.m.

a) 7560
b) 6860
c) 7960
d) 7860

View Answer

Answer (A)
Given the sides of triangle are 28 m, 45 m and 53 m
Since,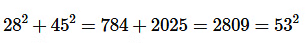 Solved Examples: Triangles | Quantitative Aptitude for SSC CGL

=> The given sides are of right angled triangle as,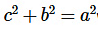 Solved Examples: Triangles | Quantitative Aptitude for SSC CGL

where a, b, c are the sides of the triangle

.=> Area of triangular field 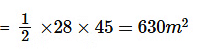Solved Examples: Triangles | Quantitative Aptitude for SSC CGL

=> Cost of sowing seeds =

Question 7: In a triangle PQR, internal angular bisectors of $∠ 𝑄$ and $∠ 𝑅$ intersect at a point O. If $∠ 𝑃$ = $110 \circ$ then what is the value of $∠ 𝑄 𝑂 𝑅$ ?
a) $125 \circ$
b) $135 \circ$
c) $145 \circ$
d) $115 \circ$

View Answer

Answer (C)

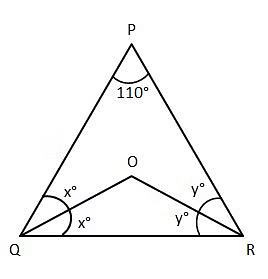
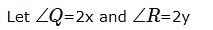
Sum of angles in a triangle=180
2x+2y+110=180
2x+2y=70
x+y=35
Similarly in the triangle QOR we have

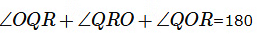
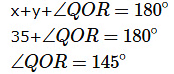
Solved Examples: Triangles | Quantitative Aptitude for SSC CGL

Question 8: In a triangle XYZ, XA is the angle bisector onto YZ. If the semiperimeter of the triangle is 12 and XY=12 ,YZ=6 then what is the ratio of YA:AZ ?

a) 2:3
b) 2:1
c) 1:2
d) 3:2

View Answer

Answer (B)

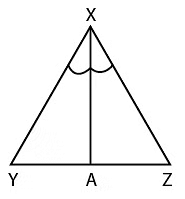
In triangle XYZ we have s=12
(x+y+z)/2 =12
x+y+z=24
12+6+y=24
y=6
Angle bisector divides the opposite side in the ratio of other sides i.e
XY/XZ=YA/AZ
YA/AZ=12/6
YA/AZ=2:1

Question 9: In a triangle ABC, AX is the angle bisector onto BC. If the semiperimeter of the triangle is 9 and AB=4 ,BC=6 then what is the ratio of BX:XC ?

a) 2:3
b) 2:1
c) 1:2
d) 3:2

View Answer

Answer (C)

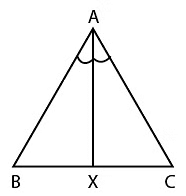
In triangle ABC we have s=9
(a+b+c)/2 =9
a+b+c=18
4+6+b=18
b=8
Angle bisector divides the opposite side in the ratio of other sides i.e
AB/AC=BX/XC
BX/XC=4/8
BX/XC=1:2

Question 10: In an equilateral triangle,if h-R=15 cm where h=height of the triangle and R=circumradius then what is the area of the triangle ?

a) 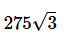Solved Examples: Triangles | Quantitative Aptitude for SSC CGL
b)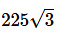
c)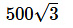
d)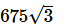

View Answer

Answer (D)

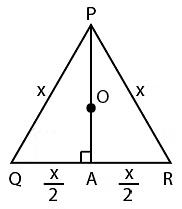
In an equilateral triangle,all the points such as orthocentre,centroid,circumcenter coincide.
Let the triangle be PQR and the circumcentre be O. let median intersect QR at A
Centroid divides median in the ratio 2:1.PA=h,OA=R
OA=15 cm
Therefore (PO:OA)=2:1
PO:15=2:1
PO=30
PA=PO+OP
PA=30+15
PA=45
PA is also the altitude using it side of the triangle can be calculated.

The document Solved Examples: Triangles | Quantitative Aptitude for SSC CGL is a part of the SSC CGL Course Quantitative Aptitude for SSC CGL.

All you need of SSC CGL at this link: SSC CGL

	Quantitative Aptitude for SSC CGL 314 videos\|170 docs\|185 tests

Quantitative Aptitude for SSC CGL

314 videos|170 docs|185 tests

Join Course for Free

Top Courses for SSC CGL

View all

FAQs on Solved Examples: Triangles - Quantitative Aptitude for SSC CGL

1. What are the different types of triangles based on their angles?

Ans. The different types of triangles based on their angles are equilateral, isosceles, and scalene triangles.

2. How do you calculate the area of a triangle?

Ans. The area of a triangle can be calculated using the formula: Area = 1/2 * base * height.

3. What is the Pythagorean theorem and how is it used in triangles?

Ans. The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the other two sides. It is commonly used to find the length of a side in a right triangle.

4. How can you determine if three given side lengths form a triangle?

Ans. To determine if three given side lengths form a triangle, you can use the triangle inequality theorem which states that the sum of any two sides of a triangle must be greater than the third side.

5. How do you find the missing angle in a triangle?

Ans. To find the missing angle in a triangle, you can use the fact that the sum of all angles in a triangle is always 180 degrees. Subtract the known angles from 180 degrees to find the missing angle.

Related Exams

SSC CGL Quant

About this Document

	4.68/5 Rating
	Nov 22, 2024 Last updated

Document Description: Solved Examples: Triangles for SSC CGL 2024 is part of Quantitative Aptitude for SSC CGL preparation. The notes and questions for Solved Examples: Triangles have been prepared according to the SSC CGL exam syllabus. Information about Solved Examples: Triangles covers topics like and Solved Examples: Triangles Example, for SSC CGL 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Solved Examples: Triangles.

Introduction of Solved Examples: Triangles in English is available as part of our Quantitative Aptitude for SSC CGL for SSC CGL & Solved Examples: Triangles in Hindi for Quantitative Aptitude for SSC CGL course. Download more important topics related with notes, lectures and mock test series for SSC CGL Exam by signing up for free. SSC CGL: Solved Examples: Triangles | Quantitative Aptitude for SSC CGL

Description

Full syllabus notes, lecture & questions for Solved Examples: Triangles | Quantitative Aptitude for SSC CGL - SSC CGL | Plus excerises question with solution to help you revise complete syllabus for Quantitative Aptitude for SSC CGL | Best notes, free PDF download

Information about Solved Examples: Triangles

In this doc you can find the meaning of Solved Examples: Triangles defined & explained in the simplest way possible. Besides explaining types of Solved Examples: Triangles theory, EduRev gives you an ample number of questions to practice Solved Examples: Triangles tests, examples and also practice SSC CGL tests

	Quantitative Aptitude for SSC CGL 314 videos\|170 docs\|185 tests

Quantitative Aptitude for SSC CGL

314 videos|170 docs|185 tests

Join Course for Free

Download as PDF

Explore Courses for SSC CGL exam

Top Courses for SSC CGL

Explore Courses

Signup for Free!

Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

Start learning for Free

10M+ students study on EduRev

Solved Examples: Triangles | Quantitative Aptitude for SSC CGL

Previous Year Questions with Solutions

Summary

MCQs

past year papers

Sample Paper

Exam

shortcuts and tricks

Free

Extra Questions

Important questions

Objective type Questions

ppt

Solved Examples: Triangles | Quantitative Aptitude for SSC CGL

study material

Semester Notes

Viva Questions

mock tests for examination

practice quizzes

pdf

Solved Examples: Triangles | Quantitative Aptitude for SSC CGL

video lectures

;

Additional Information about Solved Examples: Triangles for SSC CGL Preparation

Solved Examples: Triangles Free PDF Download

The Solved Examples: Triangles is an invaluable resource that delves deep into the core of the SSC CGL exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the Solved Examples: Triangles now and kickstart your journey towards success in the SSC CGL exam.

Importance of Solved Examples: Triangles

The importance of Solved Examples: Triangles cannot be overstated, especially for SSC CGL aspirants. This document holds the key to success in the SSC CGL exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

Solved Examples: Triangles Notes

Solved Examples: Triangles Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to Solved Examples: Triangles. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, Solved Examples: Triangles Notes on EduRev are your ultimate resource for success.

Solved Examples: Triangles SSC CGL Questions

The "Solved Examples: Triangles SSC CGL Questions" guide is a valuable resource for all aspiring students preparing for the SSC CGL exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study Solved Examples: Triangles on the App

Students of SSC CGL can study Solved Examples: Triangles alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the Solved Examples: Triangles, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of Solved Examples: Triangles is prepared as per the latest SSC CGL syllabus.

Education Revolution