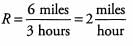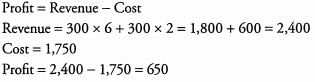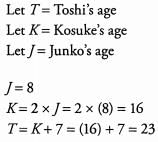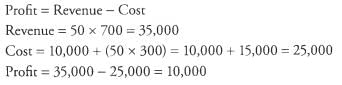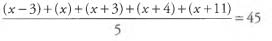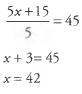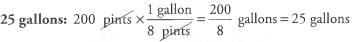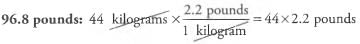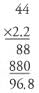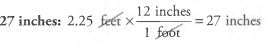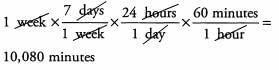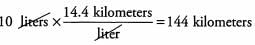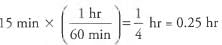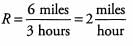Solved Examples - Word Problems - GMAT PDF Download

Section - 1
Translate and solve the following problems.
Ques 1: There are five more computers in the office than employees. If there are 10 employees in the office, how many computers are there?
Ans: Let c = number of computers
Let e = number of employees
c = e+ 5
If e = 10, then c = (10) + 5
c=15

Ques 2: If -5 is 7 more than z, what is z/4?
Ans: - 5 = z + 7
z = -12
z/4 = - 3

Ques 3: Two parking lots can hold a total of 115 cars. The Green lot can hold 35 fewer cars than the Red lot. How many cars can the Red lot hold?
Ans: Let g= the number of cars that the Green lot can hold
Let r = the number of cars that the Red lot can hold
g + r = 115
g = r - 35
(r— 35) + r= 115
2 r - 3 5 = 115
2 r= 150
r = 7 5

Ques 4: Norman is 12 years older than Michael. In 6 years, he will be twice as old as Michael. How old is Norman now?
Ans:


Ques 5: 3 lawyers earn an average of $300 per hour. How much money have they earned in total after each has worked 4 hours?
Ans:  Each lawyer worked 4 hours, earning $300 per hour.
4 x $300 = $1,200
There are 3 lawyers.
$1,200 x 3 = $3,600

Section - 2
Translate and solve the following problems.
Ques 6: Movie theater X charges $6 per ticket, and each movie showing costs the theatre $1,750. If 300 people bought tickets for a certain showing, and the theater averaged $2 in concessions (popcorn, etc.) per ticket-holder, what was the theater's profit for that showing?
Ans:


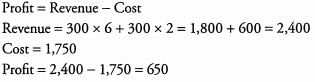
Ques 7: Toshi is 7 years older than his brother Kosuke, who is twice as old as their younger sister Junko. If Junko is 8 years old, how old is Toshi?
Ans:


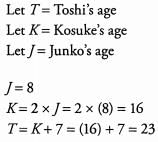
Ques 8: A plane leaves Chicago in the morning and makes three flights before returning. The first flight traveled twice as far as the second flight, and the second flight traveled three times as far as the third flight. If the third flight was 45 miles, how many miles was the first flight?
Ans:


Ques 9: It costs a certain bicycle factory $10,000 to operate for one month, plus $300 for each bicycle produced during the month. Each of the bicycles sells for a retail price of $700. The gross profit of the factory is measured by total income from sales minus the production costs of the bicycles. If 50 bicycles are produced and sold during the month, what is the factory's gross profit?
Ans:


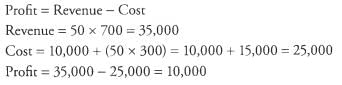
Ques 10: Arnaldo earns $11 for each ticket that he sells, and a bonus of $2 per ticket for each ticket he sells over 100. If Arnaldo was paid $2,400, how many tickets did he sell?
Ans: 

Ques 11: If the average of the five numbers x - 3, x, x +3, x +4, and x + 11 is 45, what is the value of x?
Ans:



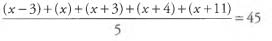
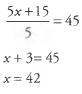
Section - 3
Translate and solve the following unit conversion problems.
Ques 12: An American football field is 100 yards long. What is this length in feet? (1 yard = 3 feet)
Ans:
 

Ques 13: How many gallons of water would it take to fill a tank with a capacity of 200 pints? (1 gallon = 8 pints)
Ans:


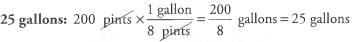
Ques 14: A 44 kilogram suitcase weighs how much in terms of pounds? (1 kilogram = 2.2 pounds)
Ans: 

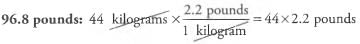
Perform long multiplication to find the product.

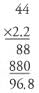
Because the two terms we’re multiplying contain, collectively, one decimal place, include a decimal place in the product. That is, place the decimal not at the end (968.) but between the 6 and the 8 (96.8).

Ques 15: The weather man reported that Boston received 2.25 feet of snow yesterday. How many inches of snow did Boston receive? (1 foot = 12 inches)
Ans:


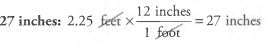
Ques 16: How many minutes are in a week?
Ans: One week contains 7 days and each of those days has 24 hours (7 x 24 = 168 total hours). Each of those hours has 60 minutes (168 x 60 = 10,080 total minutes). Using conversion ratios:


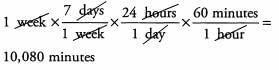
Ques 17: Joe's car can travel 36 miles per gallon of fuel. Approximately how many kilometers can the car travel on 10 liters of fuel? (5 miles = approximately 8 kilometers; 1 gallon = approximately 4 liters)
Ans: Convert miles per gallon to kilometers per liter by multiplying by the conversion ratios such that both the miles and gallons units are canceled out:

The car has 10 liters of fuel in the tank.


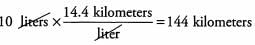
Section - 4
Translate and solve the following rate problems.
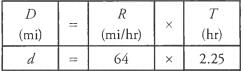
Ques 18: Jiang begins driving away from Marksville at a constant speed of 64 miles per hour. How far will she be from Marksville after 2 hours and 15 minutes?
Ans: The D = R T formula allows us to solve for Jiang’s distance. Note that the time must be converted so that it is expressed only in hours rather than hours and minutes.

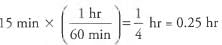
Therefore, 2 hours and 15 minutes is equivalent to 2.25 hours.



Ques 19: Tom begins the 180-mile drive from Smithton to Johnsonville at 1:00 pm. He drives at a speed of 60 miles per hour for 2 hours. He completes the rest of the drive at a speed of 45 miles per hour. At what time will he arrive in Johnsonville?
Ans: To solve this problem, we can split Tom’s journey into two portions: the first portion when he traveled 60 miles per hour and the second portion when he traveled 45 miles per hour.
For the first portion, we know that Tom traveled for 2 hours at 60 miles per hour. We can use these values in the D = R T formula to figure out how far he went.

Since Tom traveled 120 miles during the first portion of his journey he has 180 - 120 = 60 miles to travel during the second part. We know that, during this portion, he traveled at 45 miles per hour, allowing us to use the D = RT equation to calculate how long this portion of the journey took.

Tom s entire journey took 3 hours and 20 minutes: 2 hours for the first portion and 1 hour 20 minutes for the second portion. Finally, we must add 3 hours and 20 minutes to Toms starting time of 1:00 pm to calculate when Tom completed his journey, 4:20 pm.

Ques 20: If Roger walks to a store that is 3 miles away in 2 hours, and then runs home along the same path in 1 hour, what is Roger's average rate, in miles per hour, for the round trip?
Ans:  We can find the average rate by dividing the total distance traveled by the total time spent traveling. In this case, Roger travels 3 miles to and back from a store, covering a total of 6 miles in 3 hours. Thus, we can calculate his average rate using the relationship