Solved Numericals for Gauss, Stokes and Green's Theorem | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) PDF Download
Solved Numericals
Q1: Let C be the curve of intersection of the cylinder x2 + y2 = 4 and the plane z - 2 = 0. Suppose C is oriented in the counterclockwise direction around the 𝑧-axis, when viewed from above. If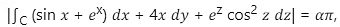
then the value of 𝛼 equals _______.
Ans: 16
C is the curve of intersection of the cylinder x2 + y2 = 4 and the plane z − 2 = 0
So, S : x2 + y2 = 4
Also, 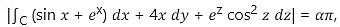
Hence 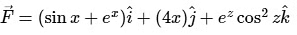
So, curl 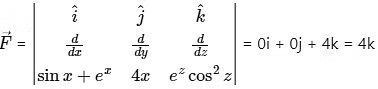
Hence  =
=
Now, S is a circle of radius 4
So, putting x = 2cosθ, y = 2sinθ we get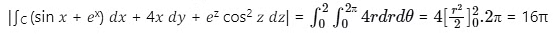
Therefore απ = 16π while implies α = 16.
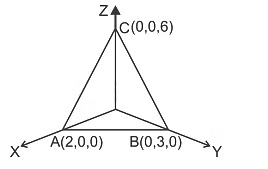
Q2. By applying Stokes theorem, the value of 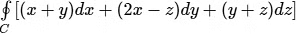 where C is the boundary of the triangle with vertices (2, 0, 0), (0, 3, 0) and (0, 0, 6), is
where C is the boundary of the triangle with vertices (2, 0, 0), (0, 3, 0) and (0, 0, 6), is
Solution: By stokes theorem: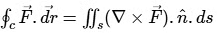
Calculation:
Given:
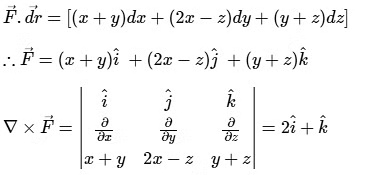
Equation of the plane through A, B, C is
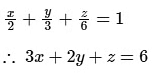
∴ ϕ = 3x + 2y + z - 6 represents equation of the surface.
Vector normal to the surface is given by gradient:
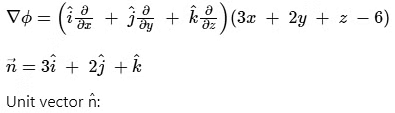

A (2, 0, 0), B (0, 3, 0) and C (0, 0, 6)
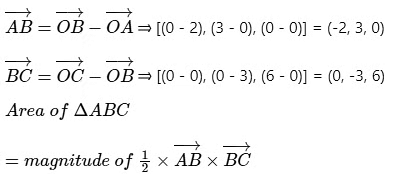
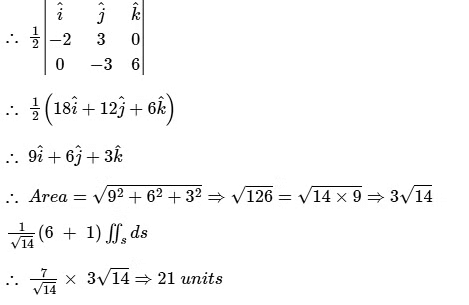
Q3. If C is the circle x2 + y2 = 1 taken in anti-clockwise direction then ∫c[(x2015 y2016 + 2014y) dy + (x2016 y2015 + 2017x) dy] will be
Solution: Green's theorem: Let C be a positively oriented, piecewise smooth, simple closed curve in the plane and let D be a region bounded by C. If P(x,y) and Q(x,y) have continuous first partial derivative on an open region that contains D, Then
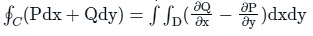
∫c[(x2015 y2016 + 2014y) dy + (x2016 y2015 + 2017x) dy]
Use green's theorem
∫ ∫c (2016 x2015 y2015+ 2017 - 2016 x2015 y2015 -2014) dx dy
= 3 ∫ ∫c ds
= 3 x area of circle
= 3π
Q4: The area of the region enclosed by a simple closed curve C will be _________.
Solution: Green's Theorem:
Let C be the positively oriented, smooth, and simple closed curve in a plane, and S be the region bounded by the C. If M and N are the functions of (x, y) defined on the open region containing S, then:
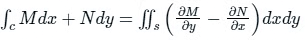
Using Green's theorem,

Putting M = y and and N = - x, we get:
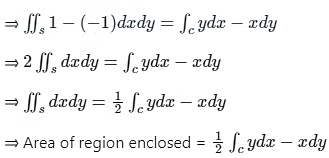
∴ The area of the region enclosed by a simple closed curve C will be 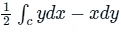 .
.
Q5. The value of 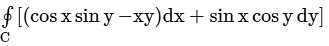 where C is the circle x2 + y2 = 1, is:
where C is the circle x2 + y2 = 1, is:
Solution: Green's Theorem:
Let C be the positively oriented, smooth, and simple closed curve in a plane, and S be the region bounded by the C. If M and N are the functions of (x, y) defined on the open region containing S, then:
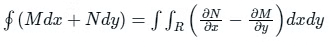
Green Theorem is useful for evaluating a line integral around a closed curve C.
Calculation:
We have,
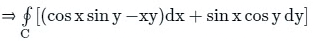 On comparing, we get⇒ M = cos x sin y - x y
On comparing, we get⇒ M = cos x sin y - x y
⇒ N = sin x cos y
On differentiating M partially with respect to 'y'

On differentiating N partially with respect to 'x'
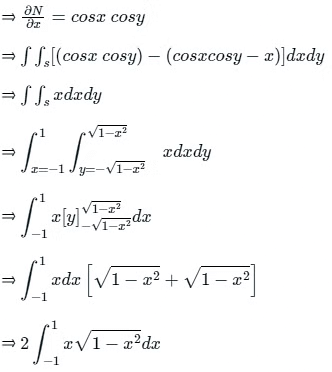
⇒ Let 1 - x2 = t
⇒ On differentiating, we get
⇒ - 2x dx = dt
When x = -1
⇒ 1 - 1 = 0 = t
When x = 1
⇒ 1 - 1 = 0 = t
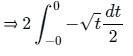 ⇒ 2 × 0⇒ 0
⇒ 2 × 0⇒ 0
Q6. Evaluate ∮c y3dx - x3dy where c is positively oriented circle of radius 2 centered at origin.
Solution:
Calculations:
In this particular case, it's cleaner to apply Green's Theorem in polar coordinates. The equality of the line integral around the positively oriented circle of radius 2 centered at origin to a double integral over the region D enclosed by the curve is as follows:
∮C P dx + Q dy = ∫∫D (dQ/dx - dP/dy) dA
We first need to compute dQ/dx and dP/dy:
dQ/dx = d(-x3)/dx = -3x2 dP/dy = d(y3)/dy = 3y2
Then, dQ/dx - dP/dy = -3x2 - 3y2
In polar coordinates, x = rcos(θ) and y = rsin(θ), and the area element dA in polar coordinates is r dr dθ.
Replacing x and y with these and simplifying gives:
dQ/dx - dP/dy = -3r2(cos2(θ) + sin2(θ)) = -3r2.
So, by Green's Theorem, the line integral ∮C P dx + Q dy is equal to the double integral
∫ (from 0 to 2π) ∫ (from 0 to 2) -3r2 × r dr dθ.
Compute this double integral to obtain the final result. Let's do this:
= ∫ (from 0 to 2π) [(-3/4 × r4) from 0 to 2] dθ = ∫ (from 0 to 2π) (-3/4 × 16) dθ = -12 × ∫ (from 0 to 2π) dθ = -12 × [θ from 0 to 2π] = -12 × 2π = -24π.
The value of ∮C y3 dx - x3 dy around the given circle in the positive direction is -24π.
Q7. As shown in the figure, 𝐶 is the arc from the point (3, 0) to the point (0, 3) on the circle x2 + y2 = 9. The value of the integral 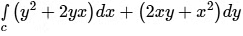 is _____ (up to 2 decimal places).
is _____ (up to 2 decimal places).
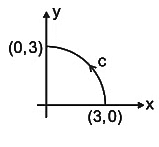 Ans: 0
Ans: 0
According to Green’s theorem
Here, M = y2 + 2yx
N = 2xy + x2
Q8. The line integral of function  in the counter clock wise direction, along the circle x
in the counter clock wise direction, along the circle x
Solution:
Green's theorem:
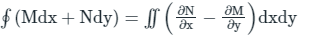
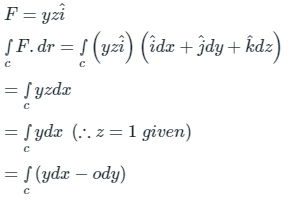
From Green’s Theorem
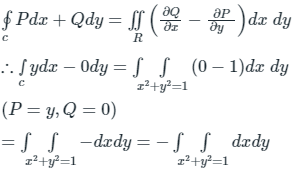
= - Area of circle (x2 + y2 = 1)
= - π × (1)2
= - π
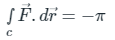
Q9. If 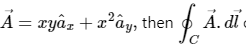 over the path shown in the figure is
over the path shown in the figure is
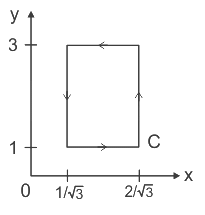 Solution:
Solution:
Green’s Theorem
If “R” is a closed region of xy plane bounded by 1 or more simple curves ‘C’ and M(x, y), N(x, y) are continuous functions in a region “R” then we have
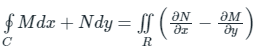
Given vector is:
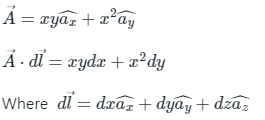
Using Green’s theorem
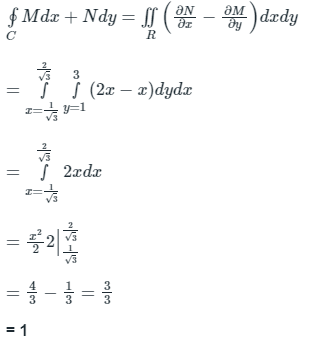
Q10. Green's theorem is used to-
Solution: Green's theorem
- It converts the line integral to a double integral.
- It transforms the line integral in xy - plane to a surface integral on the same xy - plane.
If M and N are functions of (x, y) defined in an open region then from Green's theorem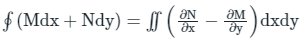
|
44 videos|109 docs|58 tests
|
FAQs on Solved Numericals for Gauss, Stokes and Green's Theorem - Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE)
| 1. How do Gauss, Stokes, and Green's Theorems relate to mechanical engineering applications? |  |
| 2. Can you give an example of how Gauss's Theorem is applied in mechanical engineering? |  |
| 3. How is Stokes's Theorem used in stress analysis in mechanical engineering? |  |
| 4. In what scenarios is Green's Theorem most commonly applied in mechanical engineering? |  |
| 5. How can knowledge of Gauss, Stokes, and Green's Theorems benefit a mechanical engineering student or professional? |  |
















