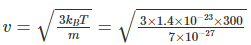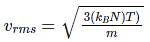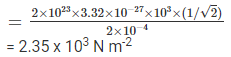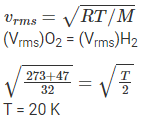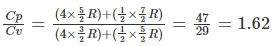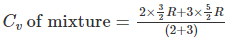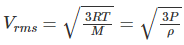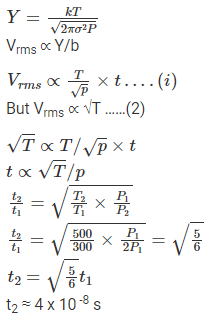Solved Questions on Kinetic Theory of Gases | Physical Chemistry PDF Download
Q.1. N moles of a diatomic gas in a cylinder is at a temperature T. Heat is supplied to the cylinder such that the temperature remains constant but n moles of the diatomic gas get converted into monoatomic gas. What is the change in the total kinetic energy of the gas?
(a) 0
(b) (5/2)nRT
(c) (½)nRT
(d) (3/2)nRT
Correct Answer is Option (c)
Initial kinetic energy of the system Ki = (5/2)RTN
Final kinetic energy of the system Kf = (5/2)RT(N-n) + (3/2)RT(2n)
Kf – Ki =ΔK = nRT(3 – 5/2) = (½)nRT
Q.2. The value closest to the thermal velocity of a Helium atom at room temperature (300 K) in m s–1 is [kB = 1.4 × 10–23 J/K; mHe = 7 × 10–27 kg]
(a) 1.3 × 103
(b) 1.3 × 105
(c) 1.3 × 102
(d) 1.3 × 104
Correct Answer is Option (a)
(3/2)kBT = ½mv2
= 1.3 x 103 ms-1
Q.3. The temperature, at which the root mean square velocity of hydrogen molecules equals their escape velocity from the earth, is closest to
[Boltzmann constant, kB = 1.38 × 10–23 J/K,
Avogadro Number, NA = 6.02 × 1026/ kg,
Radius of Earth: 6.4 × 106 m,
Gravitational acceleration on Earth = 10 m s–2]
(a) 104 K
(b) 800 K
(c) 650 K
(d) 3 × 105 K
Correct Answer is Option (a)
The escape speed of the molecule,Root mean square velocity,
So for ve = vrms ⇒ 2gR = 3(kBN)T/m
T = 2gRm/3kBN = (2 x 10 x 6.4 x 106 x 2 x 10-3)/(3 x1.38 x 10-23 x 6.02 x 1023) = 104 K
Q.4. Cooking gas containers are kept in a lorry moving with uniform speed. The temperature of the gas molecules inside will
(a) increase
(b) decrease
(c) remain the same
(d) decrease for some, while the increase for others.
Correct Answer is Option (c)
It is the relative velocities between molecules that are important. Root mean square velocities are different from lateral translation.
Q.5. One kg of a diatomic gas is at a pressure of 8 × 104 N/m2. The density of the gas is 4 kg/m3. What is the energy of the gas due to its thermal motion?
(a) 3 × 104 J
(b) 5 × 104 J
(c) 6 × 104 J
(d) 7 × 104 J
Correct Answer is Option (b)
The thermal energy or internal energy is 5 2 U RT for diatomic gases. (degree of freedom for diatomic gas = 5)
But PV = RT
V = mass/density = 1kg/(4 kg/m3) = (¼)m3
P = 8 x 104 N/m2
U = (5/2) x 8 x 104 x ¼ = 5 x 104 J
Q.6. The mass of a hydrogen molecule is 3.32 × 10–27/ kg. If 1023 hydrogen molecules strike, per second, a fixed wall of area 2 cm2 at an angle of 45° to the normal, and rebound elastically with a speed of 103 m s–1, then the pressure on the wall is nearly
(a) 2.35 × 103 N m–2
(b) 4.70 × 103 N m–2
(c) 2.35 × 102 N m–2
(d) 4.70 × 102 N m–2
Correct Answer is Option (a)
As pi = pf
Net force on the wall,
F = dp/dt = 2npfcos450 = 2nmvcos450
Here, n is the number of hydrogen molecules striking per second.
Pressure = F/A = (2nmvcos450)/Area
Q.7. The specific heats, CP and CV of gas of diatomic molecules, A, is given (in units of J mol–1 K–1) by 29 and 22, respectively. Another gas of diatomic molecules, B, has the corresponding values 30 and 21. If they are treated as ideal gases, then
(a) A has a vibrational mode but B has none.
(b) A has one vibrational mode and B has two.
(c) A is rigid but B has a vibrational mode.
(d) Both A and B have a vibrational mode each.
Correct Answer is Option (a)
Here Cp and Cv of A are 29 and 22 and Cp and Cv of B are 30 and 21.
γ = Cp/Cv = 1 + 2/f
For A, Cp/Cv = 1 + 2/f ⇒ f = 6
Molecules A has 3 translational, 2 rotational and 1 vibrational degree of freedom
For B, Cp/Cv = 1 + 2/f ⇒ f = 5
i.e., B has 3 translational and 2 rotational degrees of freedom.
Q.8. A gas mixture consists of 3 moles of oxygen and 5 moles of argon at temperature T. Considering only translational and rotational modes, the total internal energy of the system is
(a) 20 RT
(b) 12 RT
(c) 4 RT
(d) 15 RT
Correct Answer is Option (d)
U = (f1/2)n1RT + (f2/2)n2RT
U = (5/2)(3RT) + (3/2)(5RT)
U = 15RT
Q.9. An ideal gas has molecules with 5 degrees of freedom. The ratio of specific heats at constant pressure (CP) and at constant volume (CV) is
(a) 6
(b) 7/2
(c) 5/2
(d) 7/5
Correct Answer is Option (d)
An ideal gas has molecules with 5 degrees of freedom, then
Cv = (5/2)R and Cp = (7/2)R
Cp/Cv = (7/2)R/(5/2)R
Cp/Cv = 7/5
Q.10. Which of the following shows the correct relationship between the pressure ‘P’ and density of an ideal gas at constant temperature?
(a) 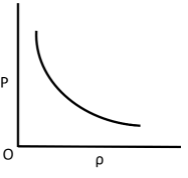
(b) 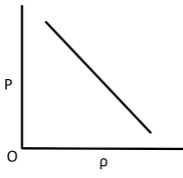
(c) 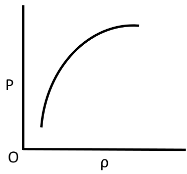
(d) 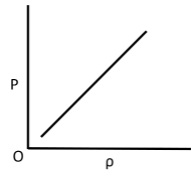
Correct Answer is Option (d)
Ideal gas equation, PV = nRT
As the temperature is constant.
PV = constant
P(m/ρ) = constant
P ∝ ρ (for given m)
Q.11. At what temperature is the root mean square velocity of a hydrogen molecule equal to that of an oxygen molecule at 47°C?
(a) 80 K
(b) –73 K
(c) 3 K
(d) 20 K.
Correct Answer is Option (d)
Q.12. A gaseous mixture consists of 16 g of helium and 16 g of oxygen. The ratio CP /CV of the mixture is
(a) 1.4
(b) 1.54
(c) 1.59
(d) 1.62
Correct Answer is Option (d)
For 16g of helium, n1 = 16/4 = 4
For 16g of oxygen, n2 = 16/32 = ½
For a mixture of gases
Cv = (n1Cv1 + n2Cv2)/(n1 + n2) where Cv = (f/2)R
Cp =( n1Cp1 + n2Cp2)/(n1 + n2) where Cp = ([f/2] + 1)R
For helium, f = 3 ,n1 = 4
For oxygen, f =5, n2 = ½
Q.13. In an ideal gas at temperature T, the average force that a molecule applies on the walls of a closed container depends on T as Tq. A good estimate for q is
(a) 2
(b) 1
(c) 4/5
(d) 4/7
Correct Answer is Option (d)
Pressure, P = ⅓(mN/V)V2rms
P = (mN)T/V
If the gas mass and temperature are constant then
P ∝ (Vrms)2 ∝ T
So, force ∝ (Vrms)2 ∝ T
I.e., Value of q = 1
Q.14. Two moles of helium gas is mixed with three moles of hydrogen molecules (taken to be rigid). What is the molar specific heat of mixture at constant volume? (R = 8.3 J/mol K)
(a) 21.6 J/mol K
(b) 19.7 J/mol K
(c) 15.7 J/mol K
(d) 17.4 J/mol K
Correct Answer is Option (b)
Cv1 of helium = (3/2)R
Cv2 of hydrogen = (5/2)R
Cv of mixture = 17.4 J/mol K
Q.15. An ideal gas is enclosed in a cylinder at a pressure of 2 atm and temperature, 300 K. The mean time between two successive collisions is 6 × 10–8 s. If the pressure is doubled and the temperature is increased to 500 K, the mean time between two successive collisions will be close to
(a) 4 × 10–8 s
(b) 3 × 10–6 s
(c) 0.5 × 10–8 s
(d) 2 × 10–7 s
Correct Answer is Option (a)
Root mean square velocity
Here,
R is the universal gas constant
M is the molar mass
P is the pressure due to gas
ρ is the density
Vrms ∝ √T
Vrms ∝ mean free path/ time between successive collisions
And mean free path
|
84 videos|142 docs|67 tests
|
FAQs on Solved Questions on Kinetic Theory of Gases - Physical Chemistry
| 1. What is the kinetic theory of gases? |  |
| 2. How does the kinetic theory of gases explain gas pressure? |  |
| 3. What is the relationship between temperature and the kinetic energy of gas molecules? |  |
| 4. How does the kinetic theory of gases explain the expansion of gases when heated? |  |
| 5. Can the kinetic theory of gases be applied to real gases? |  |