Special Theory of Relativity - 1 | Physics for IIT JAM, UGC - NET, CSIR NET PDF Download
The Issue
In this chapter we review the relevant aspects of classical mechanics, and the issues that led to the Special Theory of Relativity.
1.1 Galelian transformations and the Galeian group
Consider two observers in two reference frames, S and S ′, designated by coordinates (x, y, z) and time t, and (x′, y′, z ′ ) and time t′, respectively. Let the two reference frames be in uniform relative motion with respect to each other with constant velocity V = {vx, vy , vz }. Also, let the two reference frames differ in their orientation (which remains a constant), and differ in their origin in space and time. Then the two space and time coordinates are in general related by
 (1.1)
(1.1)
Here, R3×3 is a constant 3-parameter rotation (orthogonal 3 × 3) matrix representing the orientation of the S ′ frame with respect to S frame, and (x0, y0, z0) and t0 are the difference in their spacial and temporal origins. In all, there are 10 parameters that relate the two space and time coordinates (3 for constant spacial rotations in R3×3, 3 boost parameters -(vx, vy , vz ), 3 spacial displacements -(x0, y0, z0), and one temporal displacement-t0).
Eq. (1.1) constitutes the most general Galelian transformation connecting two coordinate systems. Any non-accelerating reference frame is defined as an inertial reference frame. Any reference frame related to any other inertial reference frame by a Galelian transformation will also be inertial.
Indeed, the significance of such transformations arises from the fact - Forces (or accelerations) seen in one inertial reference frame is the same in all inertial reference frames. More strictly, the form of the equations of mechanics are invariant with respect to such transformations. I.e.,
 (1.2)
(1.2)
Further,
 (1.3)
(1.3)
will go over to
 (1.4)
(1.4)
Some facts about the transformation in Eq. (1.1) can be immediately seen: i) Identity transformation is just a particular case of Eq. (1.1). ii) Inverse of Eq. (1.1) relating S′ to S is also of the same form. iii) If we consider two such relations relating S to S′ and S′ to S′′, respectively, say
 (1.5)
(1.5)
It can be worked out that the relation between S and S ′′ is again of the same form. I.e.,
 (1.6)
(1.6)
for suitable constant  Thus, if one considers the set of all possible transformations of the type Eq. (1.1), it forms a group under composition - the 10-parameter Galelian group.
Thus, if one considers the set of all possible transformations of the type Eq. (1.1), it forms a group under composition - the 10-parameter Galelian group.
Moral: Equations of mechanics preserve their form under Galelian transformations. Or simply, mechanics pocesses Galelian group symmetry, or is Galelian invariant.
Practically this means that we can write and follow the same equations, using one’s own lab coordinates, irrespective of our reference frame.
1.2 Maxwell’s equations do not agree
The results of the previous section constitute what is referred to as Galelian/Newtonian/Classical relativity, and consequently a relativity principle - a belief that laws of physics must be same in al l inertial reference frames, wherein the reference frames are related by transformations of the type Eq. (1.1).
However, Maxwell’s equations of electrodynamics do not show this invariance. Under the transformation x′ = x − v0t, y′ = y, z′ = z andes t′ = t, we have


Consider the wave equations in vacuum for the electric and magnetic fields, propagating in the  direction
direction


The solution is a Electro-Magnetic wave with velocity of propagation  However, under a transformation x′ = x − v0t, t′ = t, the equation
However, under a transformation x′ = x − v0t, t′ = t, the equation
 (1.13)
(1.13)
 (1.14)
(1.14)
I.e., a E-M wave of velocity c − v0, as one would expect from classical relativity. However, several experiments have shown that the speed of light in vacuum is the same, c, irrespective of the velocity of the source or velocity of the reference frame.
Practically this implies that if Maxwell’s equations are valid in on inertial reference frame, then it should not be valid for an observer in any other non-trivial inertial reference frame. I.e., electrodynamics, as expressed in the form of Maxwell’s equations, must by valid only in some specific special reference frame. However, any attempt to locate this special frame was a failure.
1.3 Possible resolutions
There are three possible resolutions to the issue:
1. Mechanics is fine and Galelian relativity is valid. But Maxwel l’s equations are wrong. If this is so then first of all we must be able to show this experimentally, and hopefully correct the equations to the ones that show the symmetry.
2. Mechanics is fine and Maxwel l’s equations are fine. But the relativity principle does not exist for electrodynamics. If this is true then doing physics will be tough. For, we may have to write up different equations for each geographical location or even each day. However, if this is indeed true we must be able to confirm this experimentally.
Every effort, running over several decades, along these two lines showed a negative result.
Maxwell’s equations were valid to the best of accuracy. The special reference frame could not be found. Curiously enough, as was mentioned earlier, the speed of light was found to be the same irrespective of the velocity of the source, or the observer2
3. Maxwel l’s equations are fine and a relativity principle exists. But, the expressions as in Eq. (1.1) are wrong.
The third possibility was the one investigated by Einstein, and the one that resolved all issues.
The Special Theory
We shall deliberately ignore the chronological development of the theory 1, and start directly from the answer.
The Postulates
The resolution came in the form of two (just two!!) postulates.
PI. The principle of relativity: Laws of physics must be the same in all inertial reference frames.
Though this assertion may sound nothing new, it has to be appreciated that, first of all, this is a postulate. Besides, the change is in its privilege, now as an apriori assertion.
The second postulate brings in some fundamental changes in our notion of space and time.
While the following sections in this chapter are devoted to a more detailed discussion on these aspects, we shall briefly define the bare minimum first, just enough material to state the postulate.
The special theory forces us to look upon space and time not independently, but as a space-time continuum. Just as we speak of a point in 3-space given by 3-coordinates, we have Events(noun) designated by 4 coordinates - 3 spacial and 1 temporal. Thus we have a 4-dimensional space-time, and every space-time point is defined as an ’Event’. For a start it may be convenent to think of these Events as usual events(verb).
Consider two Events in space-time, say  (say two firecrackers bursting in the sky at two different points at different times). Contrary to our usual notion that time intervals
(say two firecrackers bursting in the sky at two different points at different times). Contrary to our usual notion that time intervals  are independently invariant in any reference frame, we have
are independently invariant in any reference frame, we have
PII. The space time interval between two Events, defined as
 (2.1)
(2.1)
is an invariant in any inertial reference frame, where ′c′ is a universal constant whose value is roughly 3 × 108 m/s.
I.e., if the same two events are in another inertial reference frame designated by the space-time coordinates = 1, 2, then
= 1, 2, then

The speed of light happens to be ′c′.
The remaining part of the course will be confined to convincing ourselves that the special theory does indeed resolve the issues discussed in the previous chapter, and make the relevant changes in Newtonian mechanics. However, as mentioned earlier, PII changes our notion of space and time fundamentally. This chapter will detail these changes.
Space-time, Events and World Lines
In classical relativity, the instantaneous position of a particle, or an ob ject, is specified by its space coordinates, and its time evolution is illustrated by a tra jectory it traces out in space. But, PII puts space and time in equal footing, thus prohibiting looking upon the two independently. Consequently, The tra jectory of, say, a particle in space becomes a tra jectory connecting space-time ’Events’. Such a tra jectory shall be called a ’World Line’. The four coordinates do not have the same dimension, however. This is taken care of by scaling the time axis with the universal constant ′c′.
A few examples are shown in Figures 2.1 and 2.2.




Figure 2.1: Two simple situations and their world line view: a) an ob ject at rest, and c) a object in uniform motion along x direction in space, and their respective world lines c) and d). World lines of ob jects in uniform motion are straight lines. y and z directions are not shown in b) and d).


Figure 2.2: a) The world line of a accelerating ob ject, moving in the x direction. The curvature of the world line is a measure of its acceleration. The other two spacial directions are suppressed for simplicity. b) The world line of a planet orbiting in the x − y plane. The world line for the planet is a helix (i.e, if the orbit is circular).
Thus even an ob ject at rest is represented by a line. In some sense, even an ob ject at rest is moving in space time. Two observations are immediate: a) Ob jects in uniform motion in a inertial (henceforth a default unless specified explicitly) reference frame are represented by straight world lines in the space-time diagram drawn in any reference frame. b) Ob jects that are accelerating will have curved world lines. More specifically, the acceleration at a point (ct, x, y, z ) will be given by the curvature of the world line at that point.
2.3 Two Events in two different inertial frames
In comparing two points in space, Galelian relativity was wound around the postulate that the spacial separation between the two points will be the same for any two observers. And so was the case for temporal separation between two events.
2.3.1 Correspondence
Consider two events A and B , with coordinates (ct1, x1) and (ct2, x2) (y and z coordinates being same for simplicity) in a reference frame S . Say an ob ject starts at A and reaches B with uniform velocity v in the  direction as in Figure 2. Then
direction as in Figure 2. Then
 (2.3)
(2.3)
Let S ′ be another reference frame moving with respect to S with some velocity such that the same two events in S ′ are  and the velocity of the ob ject v′. From PII we have
and the velocity of the ob ject v′. From PII we have
 (2.4)
(2.4)
When velocities v1 and v2 are small compared to c, Eq. (2.4) reduces to
 (2.5)
(2.5)
or simply, one gets back Galelian relativity. Indeed, practically relativistic effects are significant only at velocities of the order 0.5c and more.
Objects with velocity c are special
Suppose the ob ject in the previous section is moving at speed v = c in S . Then evidently,
 (2.6)
(2.6)
Consequently and v′ = c. I.e., if an ob ject is moving at speed c in some reference then it moves with the same speed c in all reference frames. Ob jects traveling with speed c are treated by space-time with a little added privilege. Hence, the velocity of light in vacuum being c, will be the same as seen from any reference frame, just as several experiments had suggested.2 Indeed, from Eq. (2.4) it follows that an ob ject moving with a speed less than (greater than) c in one reference will be seen to be moving with a speed less than (greater than) c in any reference frame. In fact, the invariance of the space-time intervals allows us to classify them into three types based on their sign:
and v′ = c. I.e., if an ob ject is moving at speed c in some reference then it moves with the same speed c in all reference frames. Ob jects traveling with speed c are treated by space-time with a little added privilege. Hence, the velocity of light in vacuum being c, will be the same as seen from any reference frame, just as several experiments had suggested.2 Indeed, from Eq. (2.4) it follows that an ob ject moving with a speed less than (greater than) c in one reference will be seen to be moving with a speed less than (greater than) c in any reference frame. In fact, the invariance of the space-time intervals allows us to classify them into three types based on their sign:
2.3.3 Time like, space like and light like intervals: Causality
Two events are said to be time like, space like or light like separated if their space-time intervals are such that  respectively. The primary significance being that they maintain this classification in any reference frame.
respectively. The primary significance being that they maintain this classification in any reference frame.
We wish to see how the spacetime separation between events look like in different reference frames. Of two events A and B , let A coincide with the origin in two reference frames S and S ′ (i.e, the two reference frames coincide at their origin). Given B = (ct; x, y, z ) in frame S , we wish to see where B = (ct′, x′, y′, z ′) can possibly be in S ′. Since the space time coordinates of A being the origin, we have,
 (2.7)
(2.7)
If the two events are time like,space like and light like separated, then we have
 and
and  respectively, leading to
respectively, leading to
 (2.8)
(2.8)
The equations may be recognized as paraboloid, hyperboloid and a hyper cone separating the two.
This is illustrated in the {ct, x, y} space in the Figure 2.3. If an event B lies in the paraboloid in one reference frame S , then it lies in the same paraboloid in any other reference frame S ′ (if S and S′ have the same origin). The same holds true for the light cone and the hyperboloid (See Figure 2.4)

Figure 2.3: The light cone attached to an event in space time (origin). The events in the future fall inside the cone in the +ve t direction. The events outside the cone are space like seperated from the origin and are not accessible. If a future event falls on the paraboloid inside the cone, then in any other reference frame (with the same origin) the event will be some other point in the same paraboloid. The actual structure is 4 dimensional. z direction is suppressed for simplicity.
An important observation with respect to time like and space like separated events concerns their time ordering. Suppose B and A are time like separated, and say t > 0, i.e, A precedes B in frame S . Then in any frame the time ordering is preserved. Causality is preserved if the events are time like separated. However, if A and B are space like separated, then it is possible that A precedes B in frame S , while B precedes A in S ′ or some other reference frame. Event B could be at B 1(see figure) in one reference frame and B 2 in another. Notice the difference between Newtonian causality and Einstein’s causality. In Newtonian causality, A and B 1 are causally connected. However, in Special relativity they are not, as in some other reference frame B 1 could be B 2.

Figure 2.4: Event B might transform to B ′ in some other reference frame S ′. However, the time ordering between events A and B is preserved (A′ = A). This is true for any two events that are time like separated. But the same is not true for events C and A, which are space like separated.
C transforms to C ′ in S ′. Since the time ordering is reversed, A precedes C in S , but is reversed in S′
The ticking of the clock at intervals t1, t2, .. are the events denoted by the dots along the time axis.
The space time interval between the first two ’ticks’ is given by
. (2.9)
(2.9)
Let S ′ be a reference frame moving with speed v in the x direction with respect to S . The two ticks of the clock in this reference frame do not happen at the same point in space. Let the two events in this frame be  (we do not bother about the y′, z ′ coordinates since they are same as the unprimed ones, the motion being in the x direction). The space time interval in this frame is given by
(we do not bother about the y′, z ′ coordinates since they are same as the unprimed ones, the motion being in the x direction). The space time interval in this frame is given by
 (2.10)
(2.10)
 (2.11)
(2.11)
Since the two intervals are same by PII, it follows that
 (2.12)
(2.12)
or
 (2.13)
(2.13)
Where  So, the times shown by a moving clock will be different from the one it shows when it is at rest. It can be seen that
So, the times shown by a moving clock will be different from the one it shows when it is at rest. It can be seen that 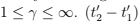
is the time interval between two ’ticks’ in a frame in which the clock is moving. From Eq. (2.13) it follows that  . Moving clocks run slower by a factor γ.
. Moving clocks run slower by a factor γ.
Definition: The Proper time between two events is defined as the time interval between the events in a frame in which the two events happen at the same place. The time shown by a clock in a reference frame in which the clock is at rest is the Proper time shown by the clock. Evidently, proper time is not defined between two events that are space like separated.
FAQs on Special Theory of Relativity - 1 - Physics for IIT JAM, UGC - NET, CSIR NET
| 1. What is the Special Theory of Relativity? |  |
| 2. How does the Special Theory of Relativity contradict classical physics? |  |
| 3. What is the significance of Einstein's equation E=mc^2 in the Special Theory of Relativity? |  |
| 4. How does the Special Theory of Relativity affect our understanding of time? |  |
| 5. Can the Special Theory of Relativity be experimentally tested? |  |

















