Square Root Tricks for 3, 4 & 5 Digit Numbers | Quantitative Aptitude for SSC CGL PDF Download
Introduction to Square Roots
- Definition: The square root of a number is the value that, when multiplied by itself, equals the original number. For instance, the square root of 625 is 25 because 25 × 25 = 625.
- Notation: The square root is denoted by the symbol √. For example, √9 = 3. If a number is a perfect square, its square root will always be a whole number.
Tricks to Find Square Roots
- Perfect Squares: To find the square root of a perfect square number easily, it's helpful to know the unit digits of the squares of the first ten numbers. Here are the unit digits obtained by squaring the numbers from 1 to 10:
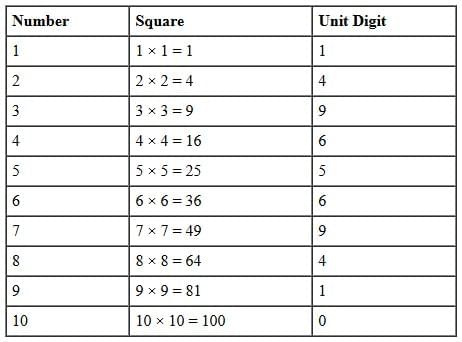
- Using the Unit Digit: When trying to find the square root of a number, the unit digit of the number can help narrow down the possibilities. For example, if the unit digit is 6, the square root could end in 4 or 6, because:
4 × 4 = 16 (unit digit 6)
6 × 6 = 36 (unit digit 6)
Follow the steps given below to find the square root of the large numbers.
Step 1: Pair the digits starting from right to left.
Step 2: Match the unit digit of the number from the chart and determine the possible values of the square root of the unit digit.
Step 3: Consider the first pair of digits. Let it be “n”.
Step 4: Determine between which two squares this number lies, √a² < n < √b². This concludes that a < n < b. Thus, the tens digit of the desired square root is “a”.
Step 5: As referred to in the chart of squares, there are only two numbers whose squares do not repeat i.e., 5 and 10. Check if the unit digit obtained in step 2 is any of them.
Step 6: Once, it is checked if the obtained number is 5 or 10, then they are written as it is, else we find out the unit digit by using the below steps.
Steps to find units digit if the unit digit obtained in step 2 is apart from 5 or 10 are:
Step 7: Now, multiply a and b.
Step 8: If ab ≤ n, then choose b, else choose a.
Square Root Tricks for 3 Digit Numbers
The square root of a three-digit number is always a two-digit number. Let us learn square root tricks for 3 digit numbers with an example.
Example: Find the square root of 196
Step 1: Split the number into two parts from right to left: 1 96
Step 2: Look at the last digit (6). Perfect squares ending in 6 usually have square roots ending in 4 or 6.
Step 3: Now look at the first part (1). It is the square of 1, so the first digit of the square root will be 1.
Step 4: Choose between 4 and 6. Since 1 is small, we pick the smaller one, which is 4.
Step 5: So, the square root of 196 is 14.
Therefore, √196 = 14.
Square Root Tricks for 4 Digit Numbers
Let us learn square root tricks for 4 digit numbers with an example.
Example: Find the square root of 2025
Step 1: Split the number into two parts from right to left: 20 25
Step 2: Look at the last two digits (25). Square roots ending in 5 usually end in 5.
Step 3: Now look at the first part (20). The square of 4 is 16 and the square of 5 is 25. Since 20 lies between 16 and 25, the first digit is 4.
Step 4: So, combine the digits: 4 and 5
Step 5: The square root of 2025 is 45
Therefore, √2025 = 45
Square Root Tricks for 5 Digit Numbers
Let us learn square root tricks for 5 digit numbers with an example.
Example: Find the square root of 10404
Step 1: Pair the digits from right to left: 1 04 04
Step 2: Look at the last two digits (04). Perfect squares ending in 4 may have roots ending in 2 or 8
Step 3: Look at the first part (1). The square of 1 is 1, so the first digit of the square root is 1
Step 4: Choose between 2 and 8. Since 1 is small, choose the smaller one: 2
Step 5: Combine the digits: 1, 0, and 2 → gives 102
Therefore, √10404 = 102
Square Root Table From 1 to 50

Examples
Q1: Find the square root of 1521
Sol:
Step 1: Pair the digits from right to left: 15 21
Step 2: The unit digit of 1521 is 1. The square roots of numbers ending in 1 can end in either 1 or 9.
Step 3: Consider the first pair of digits: 15.
15 lies between two perfect squares: 32=9 and 42=16, so the tens digit of the square root is 3.
Step 4: From steps 2 and 3, the possible square roots are 31 or 39.
Step 5: Multiply the tens digit (3) and its next number (4): 3×4=12
Step 6: Since 12 < 15, we choose the greater number from step 4:
Square root of 1521 = 39
Q2: Find the square root of 24649
Sol:
Step 1: Pair the digits from right to left: 246 49
Step 2: The unit digit is 9. So, the square root could end in 3 or 7.
Step 3: Consider the first group of digits: 246
246 lies between two perfect squares: 152=225 and 162=256 So, the tens digit of the square root is 15
Step 4: From step 2 and 3, the possible square roots are 153 or 157
Step 5: Multiply 15 and 16: 15×16=240
Step 6: Since 240 < 246, we choose the greater number from step 4:
Square root of 24649 = 157.
|
344 videos|322 docs|185 tests
|
FAQs on Square Root Tricks for 3, 4 & 5 Digit Numbers - Quantitative Aptitude for SSC CGL
| 1. What is a square root and how is it represented mathematically? |  |
| 2. What are some tricks to quickly calculate the square roots of 3-digit numbers? |  |
| 3. How can one find the square roots of 4-digit numbers efficiently? |  |
| 4. Are there any specific tips for calculating the square roots of 5-digit numbers? |  |
| 5. Why is understanding square roots important for exams like SSC CGL? |  |















