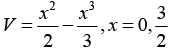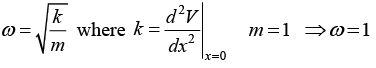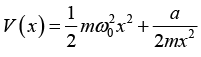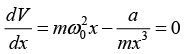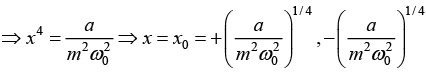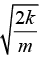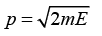Stability Analysis and Phase: Assignment | Mechanics & General Properties of Matter - Physics PDF Download
Q.1. (a) If potential energy is given by v(x) = x2/2 - x3/3. Then plot V (x) vs x.
(b) If particle of mass m = 1unit oscillates about stable equilibrium point find time period of oscillation
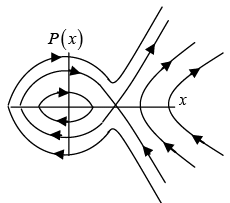
(c) Draw phase space curve for possible energy
(a)
For equilibrium dV/dx = 0 ⇒ (x - x2) = 0 ⇒ x = 0,1d2V/dx2 = (1 - 2x) = 1 > 0 at x = 0 so x = 0 is stable equilibrium point which is minima
d2V/dx2 = (1 - 2x) = 1 < 0 at x = 1 so x = 1 is unstable equilibrium Point, which is maxima
(b)
(c)
Q.2. If total energy of simple pendulum of mass m and length l is E = 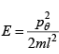 - mgl cos θ where pθ is angular momentum and V (θ) = -mgl cosθ potential energy .
- mgl cos θ where pθ is angular momentum and V (θ) = -mgl cosθ potential energy .
(a) Draw the phase space for simple pendulum assuming potential.
(b) Find the condition on energy E such that for pendulum is oscillates.
(c) Find the condition on energy E such that for pendulum will have unbounded motion.
(a)
- mglcosθ, v (θ) = - mgl cos θ
For equilibrium point
dV/dθ = 0 ⇒ = mgl sin θ = 0
θ = nπ, ⇒ θ = 0,π,2π...
For stable equilibrium point
d2V/dθ2 = mgl cos θ > 0
For q = 0, 2π, 4π ...
For unstable equilibrium point
d2V/dθ2 = mgl cos θ > 0
For θ = π, 3π, 5π ...
(b) The pendulum will do small oscillation for energy -mgl < E < mgl
Q.3. A particle of mass m is moving in a potential V(x) = 1/2 mw02x2 + a/2mx2 where ω0 and a are positive constants. Find The angular frequency of small oscillations for the simple harmonic motion of the particle about a stable point of the potential V (x).
The pendulum will execute unbounded motion E > mgl
For equilibrium point
Q.4. Consider a particle of mass m moving in one dimension under a force with potential
U(x) = k(2x3 - 5x2 + 4x) where k > 0
(a) Find the stable and unstable equilibrium point
(b) If particle oscillate about stable equilibrium point then natural frequency of oscillation is given by
(a) U(x) = k (2x3 - 5x2 + 4x), k >
dU/dx = k [6x2 - 10 x + 4] = 0 ⇒ (x - 1(6x - 4) = ⇒ x1 = 1 x2 = 2/3
To check stability= k[12x - 10] = 2k > 0 so it is stable equilibrium point.
= - 8k < 0 so it is unstable equilibrium
(b)= k[12 x - 10] = 2k > 0 ω =
Q.5. A particle of mass m trapped in one dimensional box of length a so that one edge is at x = 0 and other end at x = a. Assume after every collision of particle at x = a particle loose ΔE amount of energy. Draw phase space if initially particle has energy E.
E = p2/2m
At particle will reach first time at point x = a the energy will become E - ΔE so momentum p =.Every time particle will reach at point x = a the energy will decrease with amount ΔE
|
61 videos|23 docs|25 tests
|
FAQs on Stability Analysis and Phase: Assignment - Mechanics & General Properties of Matter - Physics
| 1. What is stability analysis? |  |
| 2. How is stability analysis important in engineering? |  |
| 3. What are the different types of stability analysis methods? |  |
| 4. What is phase in stability analysis? |  |
| 5. How does stability analysis relate to the IIT JAM exam? |  |