STOICHIOMETRY
CLASSIFICATION OF MATTER

LAWS OF CHEMICAL COMBINATION
(a) Law of conservation of mass [Lavoisier]
In a chemical change total mass remains conserved i.e. mass before the reaction is always equal to mass after the reaction.
H2 + 1/2 O2 → H2O (l)
(g) (g)
1 mole 1/2 mole 1 mole
mass before the reaction = 1 × 2 1/2 × 32 = 18 gm
mass after the reaction = 1 × 18 = 18 gm
Ex. A 15.9g sample of sodium carbonate is added to a solution of acetic acid weighing 20.0g. The two substances react, releasing carbon dioxide gas to the atmosphere. After reaction, the contents of the reaction vessel weigh 29.3g. What is the mass of carbon dioxide given off during the reaction?
Sol. The total mass of reactants taken = 15.9 20.0 = 35.9 gm. From the conservation of mass, the final mass of the contents of the vessel should also be 35.9 gm. But it is only 29.3 gm. The difference is due to the mass of released carbon dioxide gas.
Hence, the mass of carbon dioxide gas released = 35.9 - 29.3 = 6.6 gm
(b) Law of constant composition [Proust]
All chemical compounds are found to have constant composition irrespective of their method of prepration or sources.
⇒ In H2O, Hydrogen & oxygen combine in 2 : 1 molar ratio, this ratio remains constant whether it is Tap water, river water or seawater or produced by any chemical reaction.
Ex. The following are results of analysis of two samples of the same or two different compounds of phosphorus and chlorine. From these results, decide whether the two samples are from the same or different compounds. Also state the law, which will be obeyed by the given samples.
Amount P Amount Cl
Compound A 1.156 gm 3.971 gm
Compound B 1.542 gm 5.297 gm
Sol. The mass ratio of phosphorus and chlorine in compound A,
mP : mCl = 1.156:3.971 = 0.2911:1.000
The mass ratio of phosphorus and chlorine in compound B, mP : mCl = 1.542:5.297 = 0.2911:1.000
As the mass ratio is same, both the compounds are same and the samples obey thelaw of definite proportion.
(c) Law of multiple proportions [Dalton]
When one element combines with the other element to form two or more different compounds, the mass of one element, which combines with a constant mass of the other bear a simple ratio to one another.
⇒ Carbon is found to form two oxides which contain 42.9% & 27.3% of carbon respectively show that these figures shows the law of multiple proportion.
First oxide Second oxide
Carbon 42.9 % 27.3 %
Oxygen 57.1 % 72.7% Given
In th first oxide, 57.1 parts by mass of oxygen combine with 42.9 parts of carbon.
1 part of oxygen will combine with  part of carbon = 0.751
part of carbon = 0.751
Similarly in 2nd oxide
1 part of oxygen will combine with  part of carbon = 0.376
part of carbon = 0.376
The ratio of carbon that combine with the same mass of oxygen = 0.751 : 0.376 = 2 : 1
This is a simple whole no ratio this means above data shows the law of multiple proportion.
Ex. Two oxide samples of lead were heated in the current of hydrogen and were reduced to the metallic lead. The following data were obtained
(i) Weight of yellow oxide taken = 3.45 gm; Loss in weight in reduction = 0.24 gm
(ii) Weight of brown oxide taken = 1.227 gm; Loss in weight in reduction = 0.16 gm.
Show that the data illustrates the law of multiple proportion.
Sol. When the oxide of lead is reduced in the current of hydrogen, metallic lead is formed. Definitely, the loss in weight in reduction is due to removal of the oxygen present in the oxide, to combine with the hydrogen. Therefore,
the composition of the yellow oxide is: oxygen = 0.24 gm and lead = 3.45 - 0.24 = 3.21 gm.
The mass ratio of lead and oxygen, r1 = 
and the compositon of the brown oxide is : oxygen = 0.16 gm and lead = 1.227 - 0.16 = 1.067 gm.
The mas ratio of lead and oxygen, r2 = 
Now, r1 : r2 = 13.375 : 6.669 = 2.1 (simple ratio) and hence the data illustrates thelaw of multiple proportion.
(d) Law of reciprocal proportions [Richter]
When two elements combine seperately with definite mass of a third element, then the ratio of their masses in which they do so is either the same or some whole number multiple of the ratio in which they combine with each other.
This law can be understood easily with the help of the following examples.
⇒ Let us consider three elements - hydrogen, sulphur and oxygen. Hydrogen combines with oxygen to form H2O whereas sulphur combines with it to form SO2. Hydrogen and sulphur can also combine together to form H2S. The formation of these compounds is shown in fig.
In H2O, the ratio of masses of H and O is 2 : 16.
In SO2, the ratio of masses of S and O is 32 : 32. Therefore, the ratio of masses of H and S which combines with a fixed mass of oxygen (say 32 parts) will be
4 : 32 i.e. 1 : 8 ...(1)
When H and S combine together, they form H2S in which the ratio of masses of H and S is
2 : 32 i.e., 1 : 16 ...(ii)
The two ratios (i) and (ii) are related to each other as
or 2 : 1
i.e., they are whole number multiples of each other.
Thus, the ratio masses of H and S which combines with a fixed mass of oxygen is a whole number multiple of the ratio in which H and S combine together.
Ex. Methane contains 75 % carbon and 25% hydrogen, by mass. Carbon dioxide contains 27.27 % carbon and 72.73% oxygen, by mass. Water contains 11.11 % hydrogen and 88.89% oxygen, by mass. Show that the data illustrates the law of reciprocal proportion.
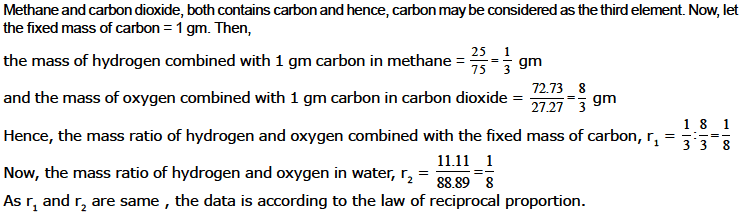
(e) Gay Lussac law of combining volumes :
When two or more gases react with one another, their volumes bear simple whole number ratio with one another and to the volume of products (if they are also gases) provided all volumes are measured under identical conditions of temperature and pressure.
⇒ When gaseous hydrogen and gaseous chlorine react together to form gaseous hydrogen chloride according to the following equation.
It has been observed experimentally that in this reaction, one volume of hydrogen always reacts with
one volume of chlorine to form two volumes of gaseous hydrogen chloride. all reactants and products are in gaseous state and their volumes bear a ratio of 1 : 1 : 2. This ratio is a simple whole number ratio.
"These are no longer useful in chemical calculations now but gives an idea of earlier methods of analysing and relating compounds by mass."
Ex. 2.5 ml of a gaseous hydrocarbon exactly requires 12.5 ml oxygen for complete combustion and produces 7.5 ml carbon dioxide and 10.0 ml water vapour. All the volumes are measured at the same pressure and temperature. Show that the data illustrates Gay Lussac's law of volume combination.
Sol. Vhydrocarbon : Voxygen : Vcarbon dioxide : Vwater vapour = 2.5 : 12.5 : 7.5 : 10.0
= 1 : 5 : 3 : 4 (simple ratio)
Hence, the data is according to the law of volume combination.
MOLE CONCEPT
Definition of mole : One mole is a collection of that many entities as there are number of atoms exactly in 12 gm of C - 12 isotope.
or 1 mole = collection of 6.02 × 1023 species
6.02 × 1023 = NA = Avogadro's No.
1 mole of atoms is also termed as 1 gm-atom, 1 mole of ions is termed as 1 gm-ion and 1 mole of molecule termed as 1 gm-molecule.
Methods of Calculations of mole
(a) If no. of some species is given, then no. of moles = 
(b) If weight of a given species is given, then no of moles = 
or = 
(c) If volume of a gas is given along with its temperature (T) and pressure (P)
use n = 
where R = 0.0821 lit-atm/mol-K (when P is in atmosphere and V is in litre.)
1 mole of any gas at STP (0°C & 1 bar) occupies 22.7 litre.
1 mole of any gas at STP (0°C & 1 atm) occupies 22.4 litre.
Atom : Atom is smallest particle which can not be divided into its constituents.
Atomic weight : It is the weight of an atom relative to one twelvth of weight of 1 atom of C-12
Relationship between gram and amu
1 amu =  wt of one C - 12 atom.
wt of one C - 12 atom.
for C 1 mole C = 12 gm = 6.023 × 1023 atoms
wt of 6.023 × 1023 atoms = 12 gm
wt of 1 atom of C =  (NA → Avogadro's number = 6.23 × 1023)
(NA → Avogadro's number = 6.23 × 1023)
1 amu =  wt of one C - 12 atom
wt of one C - 12 atom
=  gm
gm

Elemental Analysis
For n mole of a compound (C3H7O2)
Moles of C = 3n
Moles of H = 7n
Moles of O = 2n
Ex. Find the wt of water present in 1.61 g of Na2SO4. 10H2O

Average atomic weight
= ∑ % of isotope X molar mass of isotope.
The % obtained by above expression (used in above expression) is by number (i.e. its a mole%)
Molecular weight

EMPIRICAL FORMULA, MOLECULAR FORMULA
Empirical formula : Formula depicting constituent atom in their simplest ratio.
Molecular formula : Formula depicting actual number of atoms in one molecule of the compound.
Relation between the two : Molecular formula = Empirical formula × n

Check out the importance of each step involved in calculations of empirical formula.
Ex. A molecule of a compound have 13 carbon atoms, 12 hydrogen atom, 3 oxygen atoms and 3.02 × 10-23 gm of other element. Find the molecular wt. of compound.

Density :
(a) Absolute density (b) Relative density
Absolute density = 
Relative density = 
Specific gravity = 
Vapour density : It is defined only for gas.
It is a density of gas with respect to H2 gas at same temp & press
V.D =  =
=  =
=  =
= 
V.D = 
V.D = 
density of Cl2 gas with respect to O2 gas
= 
STOICHIOMETRY : Stoichiometry is the calculations of the quantities of reactants and products involved in a chemical reaction. Following methods can be used for solving problems.
(a) Mole Method (For Balance reaction)
(b) POAC method } Balancing not required but common sense ------- use it with slight care.
(c) Equivalent concept
CONCEPT OF LIMITING REAGENT.
Limiting Reagent :
It is very important concept in chemical calculation. It refers to reactant which is present in minimum stoichiometry quantity for a chemical reaction. It is reactant consumed fully in a chemical reaction. So all calculations related to various products or in sequence of reactions are made on the basis of limiting reagent.
It comes into picture when reaction involves two or more reactants. For solving any such reactions, first step is to calculate L.R.
Calculation of Limiting Reagent.
(a) By calculating the required amount by the equation and comparing it with given amount.
[Useful when only two reactant are there]
(b) By calculating amount of any one product obtained taking each reactant one by one irrespective of other reactants. The one giving least product is limiting reagent.
(c) Divide given moles of each reactant by their stoichiometric coefficient, the one with least ratio is limiting reagent. [Useful when number of reactants are more than two.]
PERCENTAGE YIELD :
The percentage yield of product = 
The actual amount of any limiting reagent consumed in such incomplete reactions is given by [% yield × given moles of limiting reagent] [For reversible reactions]
Ex. A compound which contains one atom of X and two atoms of y for each three atoms of z is made of mixing 5 gm of x, 1.15 × 1023 atoms of Y and 0.03 mole of Z atoms. Given that only 4.40 gm of compound results. Calculate the atomic weight of Y if atomic weight of X and Z are 60 and 80 respectively.


Ex. In the gravimetric determination of phosphorous, an aqueous solution of dihydrogen phosphate ion (H2PO4-) is treated with a mix of ammonium & magnesium ions to precipitate magnesium ammonium phosphate MgNH4PO4.6H2O. This is heated and decomposed to magnesium Pyrophosphate, Mg2P2O7 which is weighted. A solution of H2PO4- yielded 1.054 gm of Mg2P2O7what weight of NaH2PO4 was present originally.
NaH2PO4 → Mg2P2O7
apply POAC on P
Let wt of NaH2PO4 = w gm
moles of P in NaH2PO4 = moles of P in Mg2P2O7

SOME EXPERIMENTAL METHODS
For determination of atomic mass
Dulong's and Petit's Law :
Atomic weight × specific heat (cal/gm°C) ≈ 6.4
Gives approximate atomic weight and is applicable for metals only. Take care of units of specific heat.
Ex. 7.5 mL of a hydrocarbon gas was exploded with excess of oxygen. On cooling, it was found to have undergone a contraction of 15 mL. If the vapour density of the hydrocarbon is 14, determine its molecular formula. (C = 12, H = 1)
Sol. CxHy (x  ) + O2 → X CO2 +
) + O2 → X CO2 +  H2O
H2O
7.5 ml 15
on cooling the volume contraction = 15 ml
i.e. The volume of H2O (g) = 15 ml
V.D. of hydrocarbon = 14
Molecular wt. of CxHy = 28
12x + y = 28 ...(1)
From reaction
7.5  = 15 ⇒ y = 4
= 15 ⇒ y = 4
12 x 4 = 28
12x = 24
x = 2
Hence Hydrocalbon is C2H4.
CONCENTRATION of solution
Concentration of solution can be expressed in any of the following ways.
(a) % by wt ⇒ amount of solute dissolved in 100 gm of solution
4.9% H2SO4 by wt.
⇒ 100 gm of solution contains 4.9 gm of H2SO4
(b) % by volume ⇒ volume of solute dissolved in 100 ml of solution
x% H2SO4 by volume
⇒ 100 ml of solution contains x ml H2SO4
(c) % wt by volume ⇒ wt. of solute present in 100 ml of solution
(d) % volume by wt. ⇒ volume of solute present in 100 gm of solution.
Concentration terms
Molarity (M) : No. of moles of solute present in 1000 ml of solution.
molarity (M) = 
M = 
Molality (m)
No. of moles of solute present in 1000 gm of solvent
m =  m =
m = 
Normality (N)
No of gm equivalents of solute present in 1000 ml of solution
N =  =
= 
Formality (f)
The formality is the no. of gm -formula weights of the ionic solute present in 1000 ml of solution.
f = 
Mole fraction
The mole fraction of a perticular component in a solution is defined as the number of moles of that component per mole of solution.
If a solution has nA mole A & nB mole of B.
mole fraction of A (XA) = 
mole fraction of B (XB) = 
XA + XB = 1
Parts per million (ppm) : =  × 106
× 106 
Volume strength of H2O2
Strength of H2O2 is represented as 10V, 20V, 30V etc.
20V H2O2 means one litre of this sample of H2O2 on decomposition gives 20 It of O2 gas at S.T.P.
Decomposition of H2O2 is given as
H2O2 → H2O 
1 mole  × 22.4 It O2 at S.T.P.
× 22.4 It O2 at S.T.P.
= 34 g = 11.2 It O2 at S.T.P.
To obtain 11.2 litre O2 at S.T.P. at lest 34 gm H2O2 must be decomposed
for 20 It O2, we should decompose atleast  × 20 gm H2O2
× 20 gm H2O2
1 It solution of H2O2 contains  gm H2O2
gm H2O2
1 It solution of H2O2 contains  equivalents of H2O2
equivalents of H2O2 
Normality of H2O2 = 
Normality of H2O2(N) = 

IInd Method :
H2O2 → H2O + 
From law of equivalence
gm eq. of O2 = gm eq. of H2O2
gm eq. of O2 = moles × n factor of O2, =  =
= 
gm. eq. of H2O2 = 
and the volume of H2O2 is 1 lit.
this means 1 lit of H2O2 have  gm eq.
gm eq.
i.e. Normality N = 
Normality of H2O2
= 
Molarity of H2O2(M) = 
Strength (in g/l) : Denoted by S
Strength = molarity × mol. wt.
= molarity × 34
strength = Normality × Eq. weight.
= Normality × 17
Ex. A bottle labeled with "12V H2O2" contain 700 ml solution. If a sdudent mix 300 ml water in it what is the g/litre strenth & normality and volume strength o final solution.
Sol. N = 
meq. of H2O2 = 
let the normality of H2O2 on dilution is N
meq. before dilution = meq. after dilution
N × 1000 =  N =
N =  ×
×  = 1.5 M =
= 1.5 M = 
strength gm/lit =  = 25.5
= 25.5
volume strength = N × 5.6 = = 8.4 V Ans.
Strength of Oleum
Oleum is SO3 dissolved in 100% H2SO4. Sometimes, oleum is reported as more then 100% by weight, say y% (where y > 100). This means that (y - 100) grams of water, when added to 100 g of given oleum sample, will combine with all the free SO3 in the oleum to give 100% sulphuric acid.
Hence weight % of free SO3 in oleum = 
Ex. Calculate the percentage of free SO3 in an oleum (considered as a solution of SO3 in H2SO4) that is labelled '109% H2SO4'.
Sol. '109% H2SO4' refers to the total mass of pure H2SO4, i.e., 109 g that will be formed when 100 g of oleum is diluted by 9 g of H2O which (H2O) combines with all the free SO3 present in oleum to form H2SO4
H2O + SO3 → H2SO4
1 mole of H2O combines with 1 mole of SO3
or 18 g of H2O combines with 80 g of SO3
or 9 g of H2O combines with 40 g of SO3.
Thus, 100 g of oleum contains 40 g of SO3 or oleum contains 40% of free SO3.
Ex. A 62% by mass of an aqueous solution of acid has specific gravity 1.8. This solution is diluted such that the specific gravity of solutin became 1.2. Find the % by wt of acid in new solutiuon.

Relation ship between molarity, Molality & density of solution
Let the molarity of solution be 'M', molality be 'm' and the density of solution be d gm/m.
Molarity implies that there are M moles of solute in 1000 ml of solution wt of solution = density × volume
= 1000 d gm wt of solute = MM1
where M1 is the molecular wt of solute
wt of solvent = (1000d - MM1) gm
(1000d - MM1) gm of solvent contains M moles of solute
1000 gm of solvent have =  = Molality
= Molality
no. of moles of solute present in 1000 gm of solvent =  = Molality
= Molality
on simplyfying 
Relation ship between molality & mole fraction
consider a binary solution consisting of two components A (Solute) and B (Solvent).
Let xA & xB are the mole fraction of A & B respectively.
xA =  , xb =
, xb = 
If molality of solution be m then
 =
= 
where MB is the molecular wt of the solvent B

molality = 
m = 
Ex. An aqueous solution is 1.33 molal in methanol. Determine the mole fraction of methanol & H2O
Sol. molality = 
1.33 =  ,
,  ,
, 
⇒ xA = 0.02394 xB, xA + xB = 1
⇒ 1.02394 + xB = 1
 = 0.98, xA = 0.02 Ans.
= 0.98, xA = 0.02 Ans.
Second Method : Let wt of solvent = 1000 gm molality = 1.33
= moles of solute
mole fraction of solute =  ,
, 
mole fraction of solute = 0.02
mole fraction of solvent = 1 - 0.02 = 0.98
Ex. The density of 3 M solution of sodium thiosulphate (Na2S2O3) is 1.25 g/mL. Calculate
(i) amount of sodium thiosulphate
(ii) mole fraction of sodium thiosulphate
(iii) molality of Na and S2O32- ions
Sol. (i) Let us consider one litre of sodium thiosulphate solution.
wt. of the solution = density × volume (mL)
= 1.25 × 1000 = 1250 g.
wt. of Na2S2O3 present in 1 L of the solution
= molarity × mol. wt.
= 3 × 158 = 474 g. Ans.
wt. % of Na2S2O3 =  = 37.92%
= 37.92%
(ii) Wt. of solute (Na2S2O3) = 474 g.
Moles of solute = Ans.
Wt. of solvent (H2O) = 1250 - 474 = 776 g
Moles of solvent = 
mole fraction of Na2S2O3 = 
(iii) Molality of Na2S2O3 = 
1 mole of Na2 S2O3 contains 2 moles of Na ions and 1 mole of S2O32- ions.
molality of Na = 2 × 3.865 = 7.73 m
Molality of S2O32- = 3.865 m. Ans.
FAQs on Stoichiometry, Chapter Notes, Class 11, Chemistry (IIT-JEE & AIPMT)
| 1. What is stoichiometry in chemistry? |  |
| 2. What is the importance of stoichiometry in chemistry? |  |
| 3. How to balance a chemical equation in stoichiometry? |  |
| 4. What is the mole concept in stoichiometry? |  |
| 5. What are the applications of stoichiometry in real-life situations? |  |

|
Explore Courses for JEE exam
|

|


















