Structure Of Ionic Compounds And Defects | Physical Chemistry PDF Download
Structure of Ionic Compounds :
Simple ionic compounds are of the type AB or AB2 where A and B represent the positively and negatively charged ions respectively. (In any solid of the type Ax, By, the ratio of co-ordination number of A to B would be y:x.
- Structures of Type AB: Ionic compounds of the type AB means compounds having the positively and negatively charged ions in the ratio 1:1. These compounds can have following three t ypes of structures.
(i) Rock salt (NaCl) type
(ii) Cesium chloride (CsCl) type
(iii) Zinc blende (ZnS) type
- Structure of Ionic Compounds of the Type A2B: These are the ionic compounds having cations and anions in the ratio 1:2 Example: CaF2, SrF2, BaCl2, BaF2, PbF2, and CdF2
- Structure of Ionic Compounds of the Type A2B: These are the ionic compounds having anions and cations in the ratio 1:2 Example: Na2O, Li2O, K2O, Rb2O and Rb2S
Some special structures
WURTZITE Structure
(a) Sulphide ions have hcp arrangement and zinc ions occupy tetrahedral voids
(b) Structure has 4:4 coordination
NaCl Structure
The structure of sodium chloride (NaCl) consists of alternating Na+ and Cl- ions. The quantity of sodium ions matches that of chloride ions, and their respective radii are 95 pm and 181 pm, resulting in a radius ratio of 0.524.
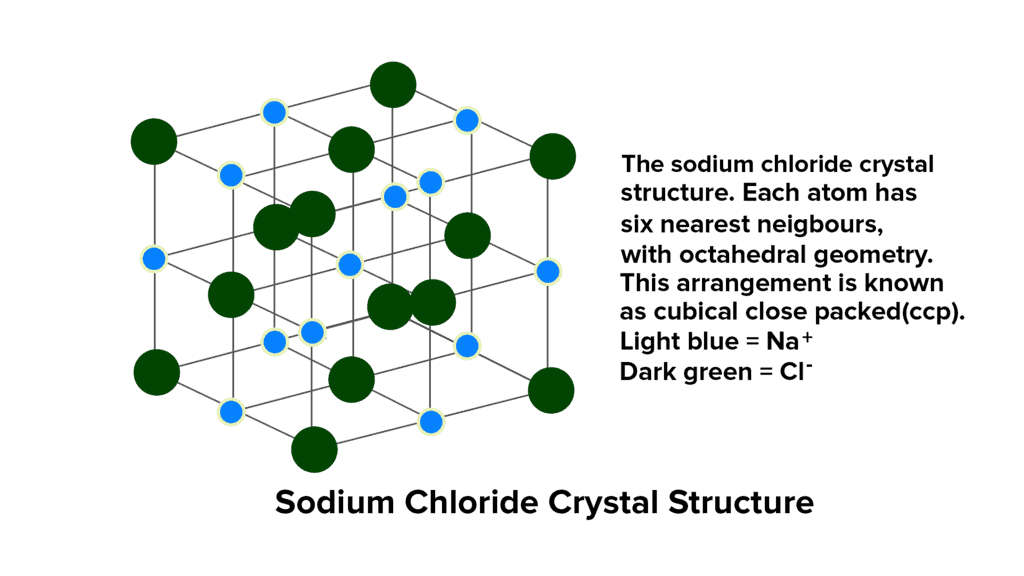
- This ratio of 0.524 suggests the presence of octahedral voids within the NaCl structure. In a typical unit cell, chloride ions are organized in cubic close packing (ccp), located at the corners and center of each face of the cube, forming a face-centered cubic arrangement (fcc).
- The sodium ions occupy all the octahedral holes within this ccp structure. Since the number of octahedral holes corresponds to the number of anions, each octahedral hole is filled by a Na+ ion, establishing the stoichiometry of NaCl as 1:1.
- Given that there are six octahedral holes surrounding each chloride ion, each Cl- ion is surrounded by six Na+ ions, and vice versa. This results in a coordination number of 6:6, indicating that each ion is coordinated with six ions of the opposite charge.
- It's worth noting that for Na+ ions to fit precisely into the octahedral holes, the radius ratio (rNa+ / rCl-) should ideally be 0.414. However, the observed radius ratio in NaCl is 0.524, surpassing this value. Consequently, to accommodate the larger Na+ ions, Cl- ions slightly move apart, creating an expanded face-centered lattice where they do not touch each other.
- The total number of NaCl units per unit cell is 4.
CsCl Structure
The caesium chloride crystal is composed of equal number of caesium (Cs+) and Chloride Cl-ions. The radii of two ions (Cs+ = 169 pm and Cl- = 181 pm) led to radius ratio of rCS+ to rCl– as 0.93 which suggest a body centred cubic structure having a cubic hole
RCS+ to RCl– = 169 / 181 = 0.93

- The chloride ion form the simple cubic arrangement and the caesium ions occupy the cubic interstitial holes. In other words Cl- ions are at the corners of a cube whereas Cs+ ion is at the centre of the cube or vice versa
- Each Cs+ ion is surrounded by 8 Cl- ions and each Cl- ion in surrounded by 8 Cs+ ions. Thus the Co – ordination number of each ion is eight.
- For exact fitting of Cs+ ions in the cubic voids the ratio rCS+ / rCl– should be equal to 0.732. However, actually the ratio is slightly larger (0.93). Therefore packing of Cl- ions slightly open up to accommodate Cs+ ions.
Number of CsCl units per unit cell is 1
Relation between radius of cation and anion and edge length of the cube, rCS to rCl = a√3/2
Other common examples of this type of structure are CsBr, CsI, TlCl, TlBr
ZnS Structure
The zinc sulphide crystals are composed of equal number of Zn+2 and S2- ions.
The radii of the two ions (Zn+2 = 74 pm and S-2 = 184 pm) led to the radius (r+ / r–) as 0.40 which suggests a tetrahedral arrangement.
rZn+2 / rS–2 = 0.40
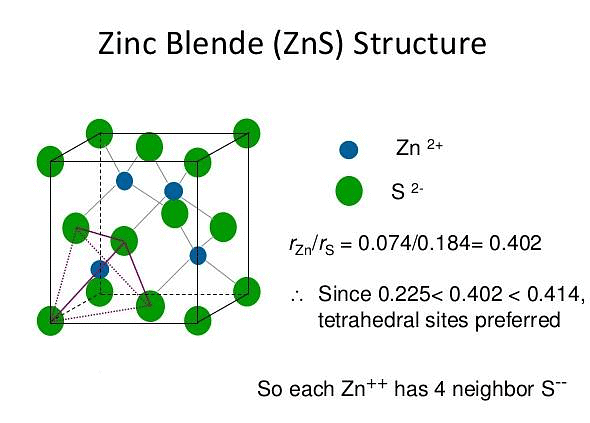
- The Zinc ions are arranged in ccp arrangement, i.e. sulphide ions are present at the corners and the centres of each face of the cube
- Zinc ions occupy tetrahedral hole. Only half of the tetrahedral holes are occupied by Zn+2 so that the formula of the zinc sulphide is ZnS i.e. the stoichiometry of the compound is 1:1 (Only alternate tetrahedral holes are occupied by Zn+2)
- Since the void is tetrahedral, each zinc ion is surrounded by four sulphide ions and each sulphide ion is surrounded tetrahedrally by four zinc ions. Thus zinc sulphide has 4:4 Co – ordination.
For exact fitting of Zn+2 in the tetrahedral holes, formed by close packing of S-2 ions, the ratio Zn+2/S-2 should be 0.225. - Actually this ratio is slightly large (0.40) There are four Zn+2 ions and four S-2 ions per unit cell as calculated below:
No. of S-2 ions = 8(at corners) × 1/8 + 6(at face centres) × 1/2 = 4
No. of Zn+2 ions = 4(within the body) × 1 = 4
Thus, the number of ZnS units per unit cell is equal to 4. Some more examples of ionic solids having Zinc blende structures are CuC, CuBr, CuI, AgI, beryllium sulphide.
Imperfections or Defects in Solids
At absolute zero, crystals tend to have a perfectly ordered arrangement. This arrangement corresponds to state of lowest energy. As the temperature increases, the crystals start deviating from the perfectly ordered arrangement. Any deviation from the perfectly ordered arrangement constitutes a defect or imperfection. These defects are sometimes called thermodynamic defects because the number of these defects depends on the temperature. Crystals may also possess addition defects due to the presence of impurities. Many properties of crystalline solids such as electrical conductivity and mechanical strength can be explained in terms of imperfections. Imperfections not only modify the properties of solids but also give rise to new properties.

The defects which arise due to the irregularity in the arrangement of atoms or ions are called atomic imperfections. The atomic defects caused by missing or misplaced ions are called point defects. If the deviations from periodicity extend over microscopic regions of the crystal they are called lattice imperfections. Lattice imperfections may extend along lines (line defects) or planes (plane defects). Line defects are also called dislocations. Various types are as follows.
(i) Stoichiometric point defects:
The compounds in which the numbers of positive and negative ions are exactly in the ratios indicated by their chemical formula are called stoichiometric compounds. The defects that do not disturb the stoichiometry (the ratio of numbers of positive and negative ions) are called stoichiometric defects.
Fundamentally, they are of two types:
- Vacancy defect: When an atom is not present at their lattice sites, then that lattice site is vacant and it creates a vacancy defect. Due to this, the density of a substance decreases.
- Interstitial defect: This type of defects is caused due to the normally vacant interstitial sites in the crystal. The ions occupying the interstitial sites are called interstitials. The formation of interstitial defects is determined by the size of the interstitial ion.
A non-ionic compound mainly shows vacancy and interstitial defects. An ionic compound shows the same in Frenkel and Schottky defect.
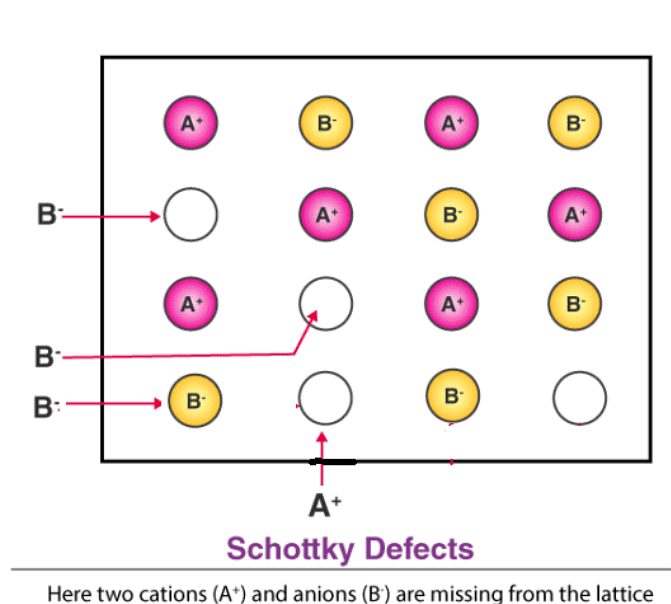
(a) Schottky Defect – Schottky defects form when the cations and anions removed from the crystal structures are in equal numbers. However, the electrical neutrality of the crystal remains unchanged because the numbers of charges removed from the crystal are equal. This type of defects occurs in crystals having cations and anions of similar sizes.
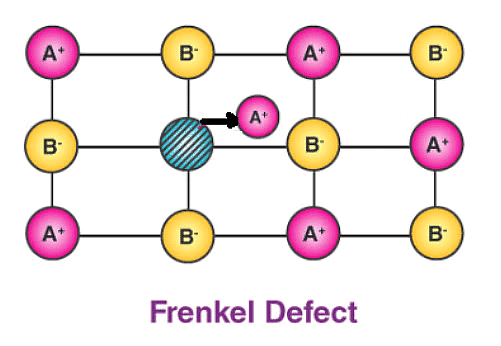
(b) Frenkel Defect – This t ype of defect is created when an ion leaves its correct latt ice site and occupies an interstitial site. Frenkel defects are common in ionic compounds which have low coordination number in which there is difference in size between positive and negative ions. For exampleZnS, AgCl, AgBr and AgI.
Consequences of stoichiometric defects
(i) The presence of those defects in the crystal makes them good electrical conductors.
(ii) The presence of holes in the Schottky type defects lowers their density.
(iii) The presence of ions in interstitial sites in the Frenkel defects increases the dielectric constant of the crystals.
(ii) Non Stoichiometric defects
There are many compounds in which the ratio of positive and negative ions present in the compound differs from that required by ideal chemical formula of the compound. In these compounds composition may vary over a wide range. The defects which disturb the stoichiometry of the compound are called
non-stoichiometric defects. These defects are either due to the presence of excess metal ions or excess non-metal ions.
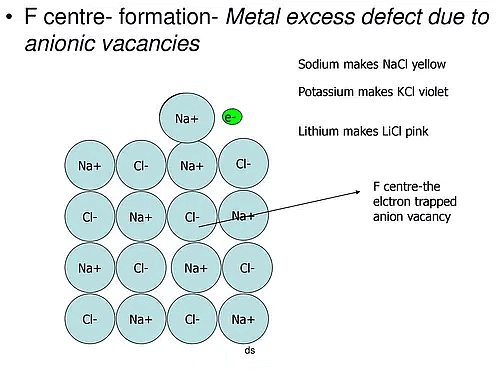
(a) Metal excess Defects due to Anion Vacancies : A compound may have excess metal ion if a negative ion is absent from its lattice site, leaving ‘hole’ which is occupied b y electron to maintain electrical neutralit y. These t ypes of defects are found in crystals which are likely to possess Schottky defects. Anion vacancies in alkali halides are produced by heating the alkali halide crystals in an atmosphere of alkali metal vapours. Under these conditions alkali metal atoms deposit on the surface of the alkali halide crystal, halide ions move to the surface and combine with metal ions. The electrons released during conversion of metal atoms into ions diffuse into the crystal and occupy the sites vacated by anions. The ‘holes’ occupied by electrons are called Fcentres (or colour centres) and are responsible for the colour of the compound and many other interesting properties. For example, the excess sodium in NaCl makes the crystal appear yellow, excess potassium in KCl makes it violet and excess lithium in LiCl makes it pink. Greater the number of Fcentres, greater is the intensity of colour. Solids containing F-centres are paramagnetic becaue the electrons occupying the ‘holes’ are unpaired.
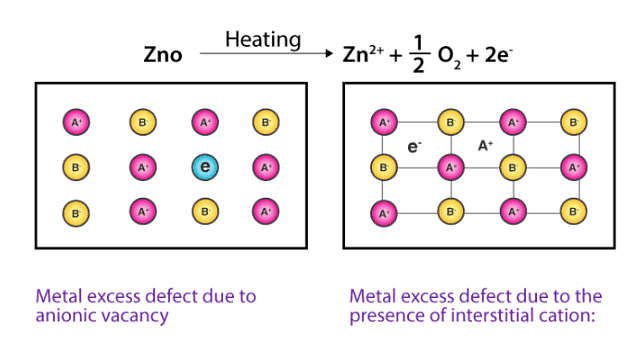
(b) Metal Excess Defects due to Interstitial Cations : Another way in which metal excess defects may occur is, if an extra positive ion is present in an interstitial site. Electrical neutrality is maintained by the presence of an electron in the interstitial site. These t ypes of defects are exhibited by the crystals which are likely to exhibit ‘Frenkel’ defects. For example, when ZnO is heated, it loses oxygen reversibly. The excess metal is accommodated in interstitial sites, with electrons trapped in the neighbourhood. The yellow colour and the electrical conductivity of the non-stoichiometric ZnO is due to these trapped electrons.
(c) Metal Deficiency due to cations vacancies : The non-stoichiometric compounds may have metal deficiency due to the absence of a metal ion from its lattice site. The charge is balanced by an adjacent ion having higher positive charge. This type of defects are generally shown b y compounds of transition metals. It ma y be ment ioned here that metal excess compounds and metal defiant compounds both act as semi-conductors. Metal excess compounds conduct electricity through normal electron conduction mechanism and are therefore n-type semiconductors. Metal deficient compounds conduct electricity through positive hole conduction mechanism and are therefore p-type semiconductors.

(iii) Point Defects due to the Presence of Foreign Atoms (Impurity defect):
Foreign atoms can occupy interstitial sites in a crystal example non-stoichiometric cuprous oxide (Cu2O) can be prepared in laboratory. In this oxide copper to oxygen ratio is slightly less than 2:1. This is due to the reason that some of the positions which were to be occupied by Cu+ ions are vacant whereas some positions are occupied b y Cu2+ ions. Defects in the ionic solids may be introduced by adding impurity ions. If the impurity ions have different valence state than that of the host ions, vacancies are created. For example addition of SrCl2 to NaCl yields solids solution where the divalent cation occupies Na+ sites and produces cat ion vacancies equal to the number of the divalent ions occupying substitution sites.
Similarly, AgCl cr ystals can be doped with CdCl2 to produce impurity defects in a likewise manner.

Designation of Planes : The orientation of a lattice plane can be described by considering the intercepts of the plane on the three basis vectors of the lattice. According to Hauy, it is possible to choose the unit lengths a, b and c along the three basis vectors such that the ratio of each of the intercepts h`, k` and l` to the corresponding unit length is either an integer or a ratio of two integers. This statement is known as the law of rational indices. The three ratios are known as the Weiss indices of the plane.
Illustration: The three plane have intercepts:
(i) a, b, ∞ (ii) 2a, b, ∞ (iii) ∞, b, ∞
The intercepts are simple multiples of unit lengths a, b, c of the basis vectors along the crystallographic axes which determine the crystal system.
Miller indices (hkl) of such planes are


(iii) Miller indices are (010)
Interplanar Distances for Cubic Systems : General formula for the interplanar spacing in the cubic system is

Where hkl are Miller indices of the planes and a is length of the cube side.
If α, β and γ are the angles which this perpendicular makes with the three axes x, y and z respectively

Bragg’s Equation

In order to have wave 1 and wave 2 in phase, we must have 2d sin θ = nλ This is known as Bragg’s equation. The constant n gives the order of reflection and is equal to the number of wavelengths in the path difference between waves reflected by adjacent planes.
|
83 videos|142 docs|67 tests
|
FAQs on Structure Of Ionic Compounds And Defects - Physical Chemistry
| 1. What is the structure of ionic compounds? |  |
| 2. How are ionic compounds formed? |  |
| 3. What are defects in ionic compounds? |  |
| 4. How do defects affect the properties of ionic compounds? |  |
| 5. Can defects be intentionally introduced in ionic compounds? |  |

|
Explore Courses for Chemistry exam
|

|


















