Electrical Engineering (EE) Exam > Electrical Engineering (EE) Notes > Signals and Systems > Study Notes for Laplace Transform & Their Properties
Study Notes for Laplace Transform & Their Properties | Signals and Systems - Electrical Engineering (EE) PDF Download
Laplace Transform
The Laplace Transform is very important tool to analyze any electrical containing by which we can convert the Integro-Differential Equation in Algebraic by converting the given situation in Time Domain to Frequency Domain.
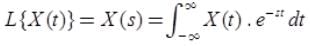 is also called bilateral or two-sided Laplace transform.
is also called bilateral or two-sided Laplace transform.- If x(t) is defined for t≥0, [i.e., if x(t) is causal], then
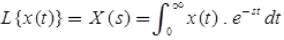 is also called unilateral or one-sided Laplace transform.
is also called unilateral or one-sided Laplace transform.
Below we are listed the Following advantage of accepting Laplace transform:
- Analysis of general R-L-C circuits become more easy.
- Natural and Forced response can be easily analyzed.
- Circuit can be analyzed with impedances.
- Analysis of stability can be done easiest way.
Statement of Laplace Transform
- The direct Laplace transform or the Laplace integral of a function f(t) defined for 0 ≤ t < ∞ is the ordinary calculus integration problem for a given function f(t) .
- Its Laplace transform is the function, denoted F(s) = L{f}(s), defined by
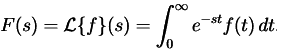
- A causal signal x(t) is said to be of exponential order if a real, positive constant σ (where σ is real part of s) exists such that the function, e- σt|X(t)| approaches zero as t approaches infinity.
- For a causal signal, if lim e-σt|x(t)|=0, for σ > σc and if lim e-σt|x(t)|=∞ for σ > σc then σc is called abscissa of convergence, (where σc is a point on real axis in s-plane).
- The value of s for which the integral
 converges is called Region of Convergence (ROC).
converges is called Region of Convergence (ROC). - For a causal signal, the ROC includes all points on the s-plane to the right of abscissa of convergence.
- For an anti-causal signal, the ROC includes all points on the s-plane to the left of abscissa of convergence.
- For a two-sided signal, the ROC includes all points on the s-plane in the region in between two abscissa of convergence.
Properties of the ROC
The region of convergence has the following properties
- ROC consists of strips parallel to the jω-axis in the s-plane.
- ROC does not contain any poles.
- If x(t) is a finite duration signal, x(t) ≠ 0, t1 < t < t2 and is absolutely integrable, the ROC is the entire s-plane.
- If x(t) is a right sided signal, x(t) = 0, t1 < t0, the ROC is of the form R{s} > max {R{pk}}
- If x(t) is a left sided signal x(t) = 0, t1 > t0, the ROC is of the form R{s} > min {R{pk}}
- If x(t) is a double sided signal, the ROC is of the form p1 < R{s} < p2
- If the ROC includes the jω-axis. Fourier transform exists and the system is stable.
Partial Fraction Expansion in Laplace Transform
- All poles have multiplicity of 1.
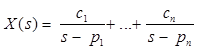
- Where, When one or more poles have multiplicity r.
In this case, X(s) has the term (s-p)r.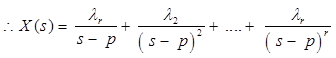
The coefficient λk can be found as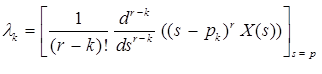
- Transfer Function of a Network having output Y(t) & Input X(t) can be computed as Laplace Transform
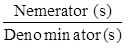
where N(s) is the Laplace transform of Output Y(t).
D(s) Laplace Transform of Input X(t).
Inverse Laplace Transform
- It is the process of finding x(t) given X(s)
X(t) = L-1{X(s)}
There are two methods to obtain the inverse Laplace transform. - Inversion using Complex Line Integral
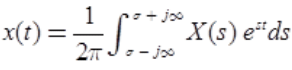
- Inversion of Laplace Using Standard Laplace Transform Table.
(Magic) A: Derivatives in t → Multiplication by s.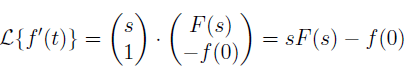


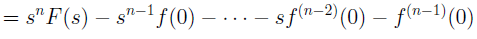
(Magic) B: Multiplication by t → Derivatives in s.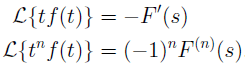
Laplace Transform of Some Standard Signals

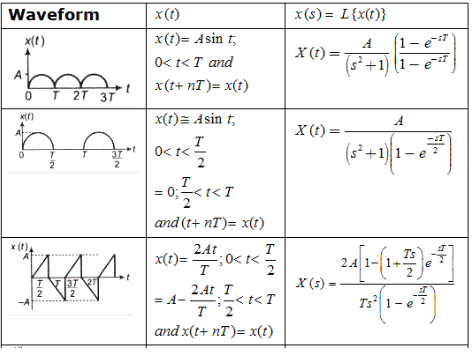
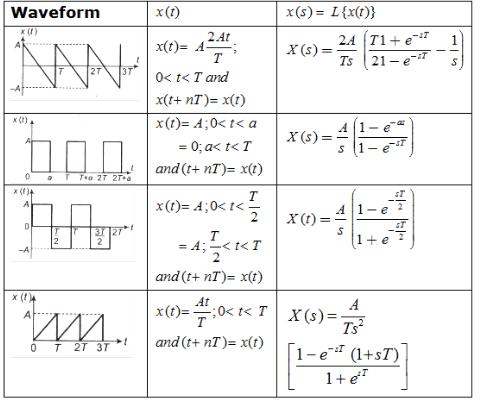
Some Standard Laplace Transform Pairs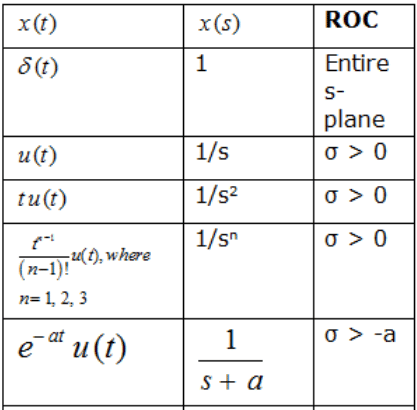


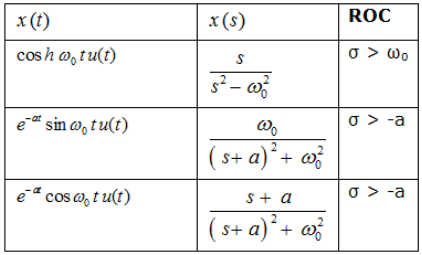
Properties of Laplace Transform


Key Points
- The convolution theorem of Laplace transform says that, Laplace transform of convolution of two time domain signals is given by the product of the Laplace transform of the individual signals.
- The zeros and poles are two critical complex frequencies at which a rational function of a takes two extreme value zero and infinity respectively.
The document Study Notes for Laplace Transform & Their Properties | Signals and Systems - Electrical Engineering (EE) is a part of the Electrical Engineering (EE) Course Signals and Systems.
All you need of Electrical Engineering (EE) at this link: Electrical Engineering (EE)
|
45 videos|70 docs|33 tests
|
FAQs on Study Notes for Laplace Transform & Their Properties - Signals and Systems - Electrical Engineering (EE)
| 1. What is the Laplace transform and how is it used in mathematics? |  |
Ans. The Laplace transform is a mathematical tool used to convert a function of time into a function of complex frequency. It is commonly used in engineering and physics to solve differential equations, as it simplifies the process of solving them by transforming them into algebraic equations.
| 2. What are the properties of Laplace transforms? |  |
Ans. The Laplace transform has several properties that make it a powerful tool in solving mathematical problems. Some of the key properties include linearity, time-shifting, scaling, differentiation, integration, convolution, and initial value theorem.
| 3. How is the Laplace transform different from the Fourier transform? |  |
Ans. While both the Laplace transform and the Fourier transform are used to analyze signals and systems, they have some fundamental differences. The Laplace transform is used for analyzing signals that are both time and amplitude-dependent, whereas the Fourier transform is used for analyzing signals that are only time-dependent.
| 4. Can Laplace transforms be used to solve differential equations? |  |
Ans. Yes, one of the main applications of Laplace transforms is solving differential equations. By applying the Laplace transform to a given differential equation, it can be transformed into an algebraic equation, which is often easier to solve. After obtaining the solution in the transformed domain, the inverse Laplace transform can be applied to obtain the solution in the time domain.
| 5. Are there any limitations or drawbacks to using Laplace transforms? |  |
Ans. While Laplace transforms are a powerful tool, they do have some limitations. One limitation is that not all functions have a Laplace transform. Additionally, the calculation of inverse Laplace transforms can sometimes be challenging, particularly for complex functions. In such cases, numerical methods or specialized techniques may be required.
Related Searches





















