Study Notes on Buoyancy | Fluid Mechanics for Mechanical Engineering PDF Download
| Table of contents |

|
| Introduction |

|
| Concept of Buoyancy |

|
| Metacentric Height (GM) |

|
| Rolling and Pitching |

|
| Illustration of the rolling and pitching of a hull |

|
Introduction
Buoyancy is also known as the buoyant force. It is the force exerted on an object that is wholly or partly immersed in a fluid.Archimedes Principle:
- Whenever a body is immersed in fluid either partially or fully, it experiences a net vertical force which is known as buoyant force.
- This buoyant force is equal to the weight of the fluid displaced by the body, and it acts upward through the centroid of the displaced volume.
Concept of Buoyancy
- The point of application of buoyant force is called the centre of buoyancy and it coincides with the centroid of the wholly submerged body of the homogenous composition.
- This buoyant force is equal to the weight of the fluid displaced by the body, and it acts upward through the centroid of the displaced volume.
- For floating bodies, the weight of the entire body must be equal to the buoyant force, which is the weight of the fluid whose volume is equal to the volume of the submerged portion of the floating body i.e.,
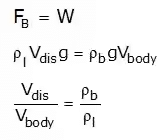
Where,FB = Buoyancy force,
Vdisp..= Displacement volume
Vbody = Total volume of the body
ρl = Density of liquid
ρb = Density of body
Stability conditions of completely submerged bodies under angular deflection:
The rotational stability of an immersed body depends on the relative locations of the centre of gravity (G) of the body and the centre of buoyancy(B).
(a). For the stable equilibrium: B should be above G.
(b). For the unstable equilibrium: B should be below G.
(c). For the neutral equilibrium: B and G coincide.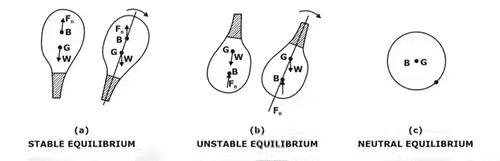 Illustration of the stability conditions of the completely submerged bodies.
Illustration of the stability conditions of the completely submerged bodies.
Metacentric Height (GM)
The metacentric height GM, which is the distance between the center of gravity (G) and the metacenter (M) which is the intersection point of the lines of action of the buoyant force through the body before and after rotation.The metacentric height using the theoretical method is given by the following formula,
GM = (BM - BG)
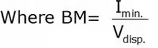
Imin. = Moment of inertia of that surface of the body which is intersected by the free surface of the liquid.
Vdisp. Displacement volume
In the above expression,
BM = Metacentric height,
BG = Calculated from geometry.
- Positive (+Ve) sign is used when the metacenter M lies above the G.
- Negative (-Ve) sign is used when the metacenter M lies below the G.
Stability conditions of partially submerged bodies under angular deflection:
The rotational stability of an immersed body depends on the relative locations of the Metacenter (M) of the body and the centre of gravity (G).
For a floating body to be in:
(a) stable equilibrium, point M should be above point G and thus GM is positive. The larger the GM is, the more stable is the floating body.
(b) unstable equilibrium, point M should be below point G and thus GM is negative.
(c) neutral equilibrium, point M should coincide with the G and thus GM = 0.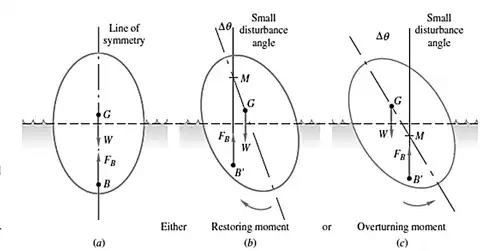 Illustration of stability conditions of the Floating bodies
Illustration of stability conditions of the Floating bodies
 |
Download the notes
Study Notes on Buoyancy
|
Download as PDF |
Rolling and Pitching
The angular displacement of a boat or ship about its longitudinal axis is known as rolling while that about its transverse axis is known as pitching. Illustration of the rolling and pitching of a hull
Illustration of the rolling and pitching of a hull

The time period of Oscillation of the floating body,
The time period of the oscillation is given by the following expression,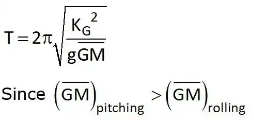
Increasing the metacentric height gives greater stability but reduces the time period of the roll so the ship will be less comfortable for the passengers.
|
56 videos|106 docs|75 tests
|


















