JEE Advanced (Subjective Type Questions): Electrostatics- 1 | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. Three charges each of value q, are placed at the corners of an equilateral triangle. A fourth charge Q is placed at the centre of the triangle. (1978)
(i) If Q = – q, will the charges at the corners move towards centre or fly away from it.
(ii) For what value of Q will the charges remain stationary?
In this situation how much work is done in removing the charges to infinity?
Ans. (i) Move towards centre;
Solution. (i)The force on charge q kept at A due to charges kept at B and C
F1 = 2F cos 30°
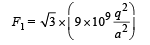
The force on q due to charge (– q) kept at D
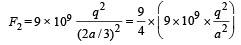
Clearly the two forces are not equal. Also as F2 > F1 the charges will move towards the centre.
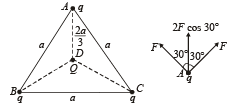
(ii) For charges to remain stationary
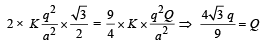
The charge Q should be negative.
The potential energy of the system is

This is the amount of work needed to move the charges to infinity.
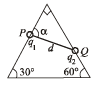
Q.2. A rigid insulated wire frame, in the form of right triangle ABC is set in a vertical plane. Two beads of equal masses m each carrying charges q1 and q2 are connected by a chord of length l and can slide without friction on the wires. Considering the case when the beads are stationary, determine :
(i) the angle α,
(ii) the tension in the chord, and
(iii) the normal reactions on the beads.
If the chord is now cut, what are the values of the charges for which the beads continue to remain stationary?
Ans. (i) 60°;
Solution. Because of equilibrium of charge q1
N1 = mg sin 60° + (T – F) sin α ... (i)
and (T – F) cos α = mg cos 60° ... (ii)
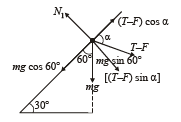
Because of equilibrium of charge q2
(T – F) sin α = mg cos 30° ... (iii)
and N2 = (T – F) cos α + mg sin 30° ... (iv)
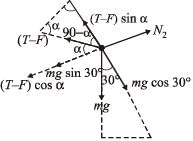
From (i) and (iii)
N1 = mg sin 60° + mg cos 30°
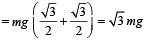
From (ii) and (iv)
N2 = mg cos 60° + mg sin 30° 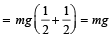
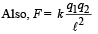
Now from eqn. (ii) and (iii), we get
(T – F)2 cos2 α + (T – F)2 sin2 α
= m2g2 cos2 60° + m2g2 cos. 30°
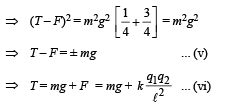
[Taking positive sign]
From (ii) and (v)
mg cos α = mg cos 60° ⇒ cos α = cos 60°
∴ α = 60°
when the string is cut, T = 0
∴ From (vi)
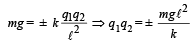
Now the charges should be unlike for equilibrium.
Q.3. A charge ‘Q’ is distributed over two concentric hollow spheres of radii ‘r’ and ‘R’ (>r) such that the surface densities are equal. Find the potential at the common centre. (1981- 3 Marks)
Ans.
Solution. Let q be the charge on the inner sphere and (Q – q) be the charge on outer sphere.
Given that surface charge densities are equal.
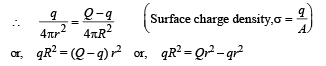
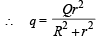
Potential at O due to inner sphere
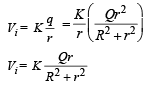
Potential at O due to outer sphere
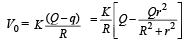
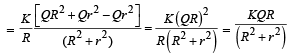
The total potential at the common centre
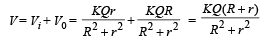
Q.4. A thin fixed ring of radius 1 metre has a positive charge 1 × 10–5 coulomb uniformly distributed over it. A particle of mass 0. 9 gm and having a negative charge of 1 × 10–6 coulomb is placed on the axis at a distance of 1 cm from the centre of the ring. show that the motion of the negatively charged particle is approaximately simple harmonic. Calculate the time period of oscillations. (1982 - 5marks)
Ans. 0.628 sec.
Solution. KEY CONCEPT : The electric field due a uniformly charged ring of radius r at a point distant x from its center on its axis is given by
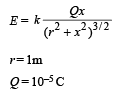
mass of particle m = 0.9 × 10–3 kg
charge on particle q = – 10–6 C
∴ Force on the negative charge q will be F = qE
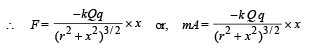
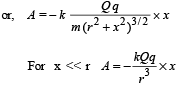
⇒ The motion is simple harmonic in nature.
Comparing the above equation with A = -ω2x we get
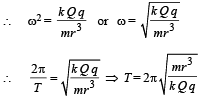
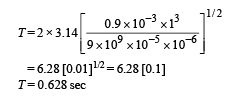
Q.5. The figure shows two identical parallel plate capacitors connected to a battery with the switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant (or relative permittivity) 3. Find the ratio of the total electrostatic energystored in both capacitors before and after the introduction of the dielectric. (1983 - 6 Marks)
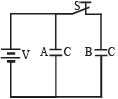
Ans. 3/5
Solution. The potential difference across each capacitor is V.
Total Energy = Energy in A + Energy in B
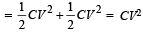
When the switch opened and a dielectric is inserted between the plates of capacitors, the new capacitance is 3C.
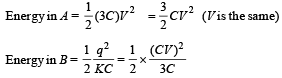
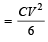 (charge on capacitor B remains same when switch is opened)
(charge on capacitor B remains same when switch is opened)
Total Energy = Energy in A + Energy in B
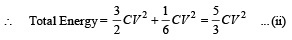
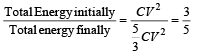
Q.6. Two fixed, equal, positive charges, each of magnitude 5 × 10–5 coul are located at points A and B separated by a distance of 6 m. An equal and opposite charge moves towards them along the line COD, the perpendicular bisector of the line AB. (1985 - 6 Marks)
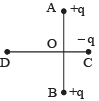
The moving charge, when it reaches the point C at a distance of 4 m from O, has a kinetic energy of 4 joules.
Calculate the distance of the farthest point D which the negative charge will reach before returning towards C.
Ans. 8.48 m
Solution. Total energy of the system of three charges when the charge –q is at C
= P.E. + K.E.
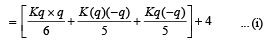
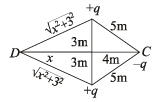
Final energy of the system of three charges when – q is at D and momentarily at rest
= P.E. + K.E.
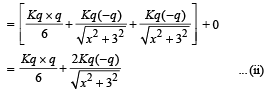
By the principle of conservation of energy from (i) and (ii), we get
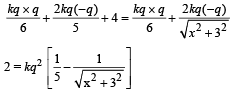
∴ x2 + 9 = 81 ∴ x = 8.48 m
Q.7. Three particles, each of mass 1 gm and carrying a charge q, are suspended from a common point by insulated massless strings, each 100 cm long. If the particles are in equilibrium and are located at the corners of an equilateral triangle of side length 3 cm, calculate the charge q on each particle. (Take g = 10 m/s2). (1988 - 5 Marks)
Ans. 3.16 × 10–9 C
Solution. Each mass will be in equilibrium under the act of three force namely tension of string, weight, resultant electrostatic force of the two other charges out of these three forces F and mg are perpendicular.
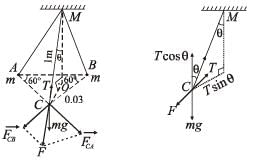
Let T make an angle θ with the vertical
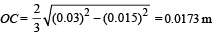
∴ OM = 0.9997
NOTE THIS STEP : Resolving T in the direction of mg and F and applying the condition of equilibrium, we get
T cos θ = mg; T sin θ = F
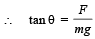 ... (i)
... (i)

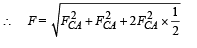

[where FCB = Force on C due to B
FCA = Force on C due to A
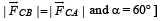
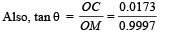 .... (iii)
.... (iii)
From (i), (ii) and (iii)

On solving, we get q = 3.16 × 10–9 C.
Q.8. A point particle of mass M is attached to one end of a massless rigid nonconducting rod of length L.
Another point particle of the same mass is attached to the other end of the rod. The two particles carry charges +q and – q respectively. This arrangement is held in a region of a uniform electric field E such that the rod makes a small angle θ (say of about 5 degree) with the field direction, fig. Find an expression for the minimum time needed for the rod to become parallel to the field after it is set free. (1989 - 8mark)
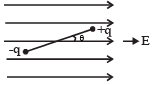
Ans.
Solutioon. Time for the dipole to align along the direction of electric field will be
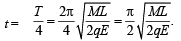
Q.9. Three concentric spherical metallic shells A, B and C of radii a, b and c (a < b <c) have surface charge densities σ , – σ and σ respectively.. (1990 -7 Marks)
(i) Find the potential of the three shells A, B and C.
(ii) If the shells A and C are at the same potential, obtain the relation between the radii a, b and c.
Ans.
Solution. Charge on Shell A = qA = σ (4πa2)
Charge on Shell B = qB = σ (4πb2)
Charge on Shell C = qC = σ (4πc2)
The potential of shell A
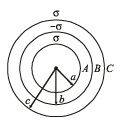
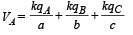
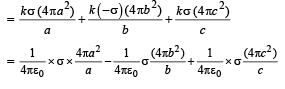
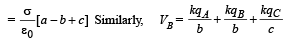
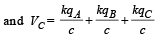
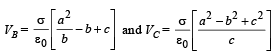
Given that VA =VC
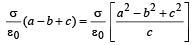
or ac – bc + c2 = a2 – b2 + c2 or c = a + b
Q.10. Two fixed charges – 2Q and Q are located at the points with coordinates (–3a, 0) and (+ 3a, 0) respectively in the x-y plane. (1991 - 4 + 2 + 2 Marks)
(a) Show that all points in the x-y plane where the electric potential due to the two charges is zero, lie on a circle.
Find its radius and the location of its centre.
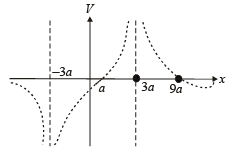
(b) Give the expression V (x) at a general point on the x - axis and sketch the function V (x) on the whole x-axis.
(c) If a particle of charge + q starts form rest at the centre of the circle, show by a short quantative argument that the particle eventually crosses the circle. Find its speed when it does so.
Ans. (a) 4a, (5a, 0)
(b)
(c)
Solution. (a) Let P be a point in the X-Y plane with coordinates (x, y) at which the potential due to charges – 2Q and + Q placed at A and B respectively be zero.
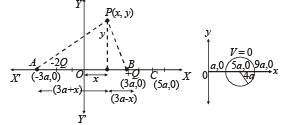
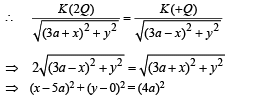
This is the equation of a circle with centre at (5a, 0) and radius 4a. Thus C (5a, 0) is the centre of the circle.
(b) For x > 3a To find V (x) at any point on X-axis, let us consider a point (arbitrary) M at a distance x from the origin.
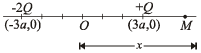
The potential at M will be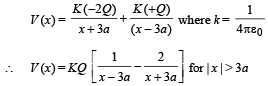
Similarly, for 0 < | x | < 3a
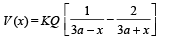
Since circle of zero potential cuts the x-axis at (a,0) and (9a, 0)
Hence, V (x) = 0 at x = a, at x = 9a
From the above expressions
V (x) → ∞ at x → 3a and V (x) → – ∞ at x → – 3a
V (x) → 0 as x → ± ∞
(c) Applying Energy Conservation
(K.E. + P.E.)centre = (K.E. + P.E.)circumference
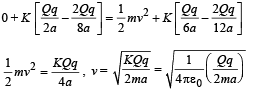
Q.11. (a) A charge of Q coulomb is uniformly distributed over a spherical volume of radius R metres. Obtain an expression for the energy of the system.
(b) What will be the corresponding expression for the energy needed to completely disassemble the planet earth against the gravitational pull amongst its constituent particles ?
Assume the earth to be a sphere of uniform mass density. Calculate this energy, given the product of the mass and the radius of the earth to be 2.5 × 1031 kg. m.
(c) If the same charge of Q coulomb as in part (a) above is given to a spherical conductor of the same radius R, what will be energy of the system ? (1992 - 10 Marks)
Ans.
Solution. (a) Let us consider a shell of the thickness dx at a distance x from the centre of a sphere
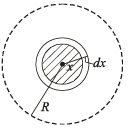
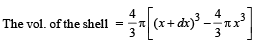
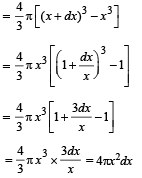
Let r be the charge per unit volume of the sphere
∴ Charge of the shell = dq = 4πx2ρdx ... (i)
Potential at the surface of the sphere of radius x
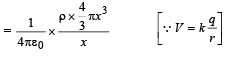
∴ Potential at the surface of the sphere of radius x = 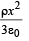
Work done in bringing the charge dq on the sphere of radius x
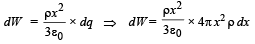
Therefore the work done in accumulating the charge Q over a spherical volume of radius R meters
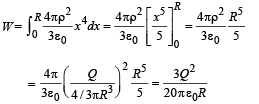
This is also the energy stored in the system.
(b) The above energy calculated is
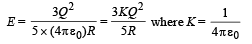
NOTE : In case of earth and gravitational pull, K may be replaced by G. Therefore the energy required to disassemble the planet earth against the gravitational pull amongst its constituent particle is the work required to make earth from its constituent particles.
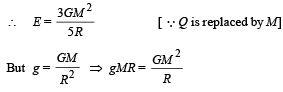
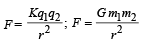
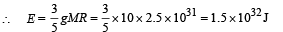
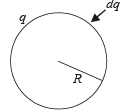
(c) During the charging process, let at any instant the spherical conductor has a charge q on its surface.
The potential at the surface 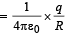
Small amount of work done in increasing charge dq more on the surface will be
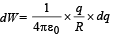
∴ Total amount of work done in bringing charge Q on the surface of spherical conductor.
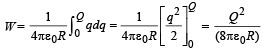
Q.12. Two par allel plate capacitor s A an d B h ave th e same separation d = 8.85 × 10–4 m between the plates. The plate area of A and B are 0.04 m2 and 0.02m2 respectively. A slab of dielectric constant (relative permittivity) K = 9 has dimensions such that it can exactly fill the space between the plates of capacitor B. (1993 - 2 + 3 + 2 Marks)
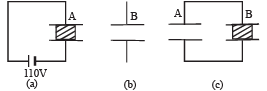
(i) The dielectric slab is placed inside A as shown in figure (a). A is then charged to a potential difference of 110V.
Calculate the capacitance of A and the energy stored in it.
(ii) The battery is disconnected and then the dielectric slab is moved from A. Find the work done by the external agency in removing the slab from A.
(iii) The same dielectric slab is now placed inside B, filling it completely. The two capacitors A and B are then connected as shown in figure (c). Calculate the energy stored in the system.
Ans. (i) 2 × 10–9 F, 1.21 × 10–5 J
(ii) 4.84 × 10–5 J
(iii) 1.1 × 10–5 J
Solution. (i) NOTE : The capacitor A with dielectric slab can be considered as two capacitors in parallel, one having dielectric slab and one not having dielectric slab. Each capacitor has an area of A/2.
The combined capacitance is
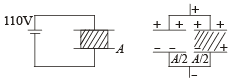
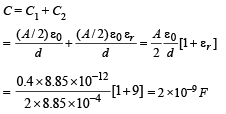
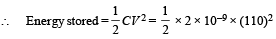
= 1.21 × 10–5 J
(ii) Work done in removing the dielectric slab = (Energy stored in capacitor without dielectric) – (Energy stored in capacitor with dielectric).
NOTE : While taking out the dielectric, the charge on the capacitor plate remains the same.
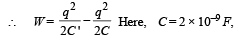
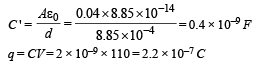
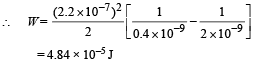

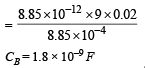
The charge on A, qA = 2.2 × 10–7 C gets distributed into two parts. ∴ q1 + q2 = 2.2 × 10–7 C also the potential difference across A = p.d. across B
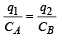
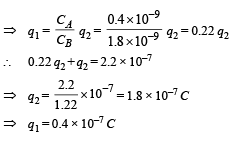
Total energy stored 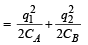
|
446 docs|929 tests
|
FAQs on JEE Advanced (Subjective Type Questions): Electrostatics- 1 - Chapter-wise Tests for JEE Main & Advanced
| 1. What is electrostatics and how does it relate to JEE Advanced? |  |
| 2. What is Coulomb's law and how is it used in electrostatics? |  |
| 3. What is an electric field and how is it calculated? |  |
| 4. What is electric potential and how does it differ from electric field? |  |
| 5. What is capacitance and how is it related to electrostatics? |  |





















