JEE Advanced (Subjective Type Questions): Limits, Continuity & Differentiability | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q. 1. 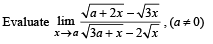
Ans. 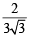
Solution.
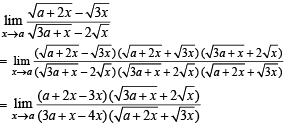
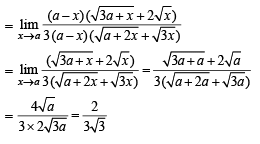
NOTE : The given limit is of the form 0/0 . Hence limit of the function can also be find out by using L' Hospital's Rule
Q. 2. f (x) is the integral of 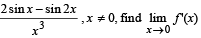
Ans. 1
Solution.
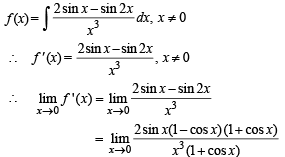
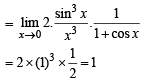
Q. 3. Evaluate : 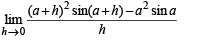
Ans. a2 cos a + 2a sin a
Solution.
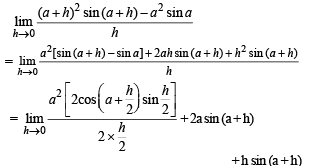
= a2 cos a + 2a sin a
Q. 4. Let f (x + y) = f (x) + f (y) for all x and y. If the function f(x) is continuous at x = 0, then show that f (x) is continuous at all x.
Solution. As f (x) is continuous at x = 0, we have
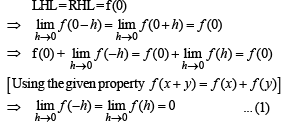
Now let x = a be any arbitrary point then at x = a,
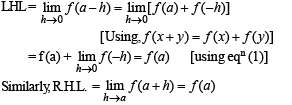
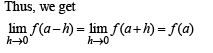
⇒ f is continuous at x = a. But a is any arbitrary point
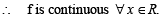
Q. 5. Use the formula 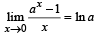 to find
to find 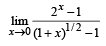
Ans. 2 ln 2
Solution.
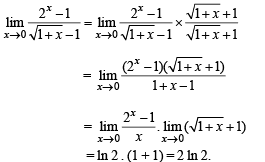
Q. 6. 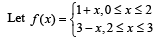
Determine the form of g(x) = f [ f(x) and hence find the points of discontinuity of g, if any
Ans. 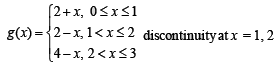
Solution. Graph of f (f (x)) is
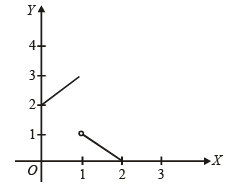
Clearly form graph f (f (x)) is discontinuous at x = 1 and 2.
Q. 7. 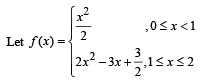
Discuss the continuity of f, f ' and f " on [ 0, 2].
Ans. f and f' are continuous and f'' is discontinuous on [0, 2]
Solution. 
Here f (x) is continuous everywhere except possibly at x = 1
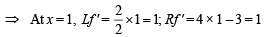
⇒ f is differentiable and hence continuous at x = 1
∴ f (x) is continuous on [0, 2]
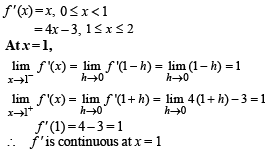

Q. 8. Let f (x) = x3 - x2 + x + 1 and

Discuss the continuity and differentiability of the function g(x) in the interval (0, 2).
Ans. cont. on (0, 2) and differentiable on (0, 2) – {1}
Solution. Given f (x) = x3 – x2 + x + 1
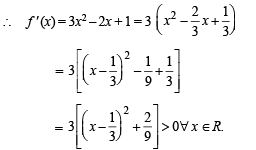
Hence f (x) is an increasing function of x for all real values of x.
Now max 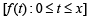 means the greatest value of
means the greatest value of  which is obtained at t = x, since f (t) is increasing for all t.
which is obtained at t = x, since f (t) is increasing for all t.
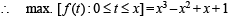
Hence the function g is defined as follows :
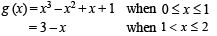
Now it is sufficient to discuss the continuity and differentiability of g (x) at x = 1. Since for all other values of x, g (x) is clearly continuous and differentiable, being a polynomial function of x.
We have, g (1) = 2
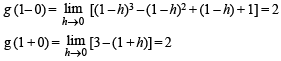
Hence g (x) is continuous at x = 1 Now,
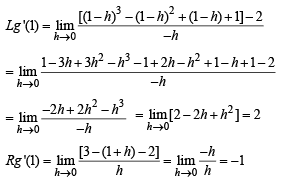
Since  the function g (x) is not differentiable at x = 1 Hence g (x) is continuous on (0, 2). It is also differentiable on (0, 2) except at x = 1.
the function g (x) is not differentiable at x = 1 Hence g (x) is continuous on (0, 2). It is also differentiable on (0, 2) except at x = 1.
Q.9. Let f (x) be defined in the interval [–2, 2] such that
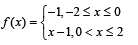
and g(x) = f (|x |) + |f (x)|
Test the differentiability of g(x) in (– 2, 2).
Ans. not differentiable at x = 1
Solution.
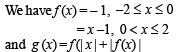
Hence g(x) involves | x | and | x –1| or | – 1| = 1
Therefore we should divide the given interval (–2, 2) into the following intervals.
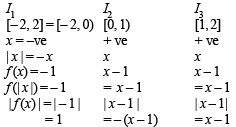
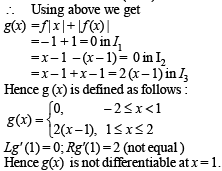
Q.10. Let f (x) be a continuous an d g (x) be a discontinuous function. prove that f (x) + g (x) is a discontinuous function.
Solution. Let h (x) = f (x) + g (x) be continuous.
Then, g (x) = h (x) – f (x)
Now, h (x) and f (x) both are continuous functions.
∴ h (x) – f (x) must also be continuous. But it is a contradiction as given that g (x) is discontinuous.
Therefore our assumption that f (x) + g (x) a continous function is wrong and hence f (x) + g (x) is discontinuous.
Q.11. Let f (x) be a function satisfying the condition f (– x)= f (x) for all real x. If f ' (0) exists, find its value.
Ans. f ' (0) = 0
Solution. Given that f (x) is a function satisfying
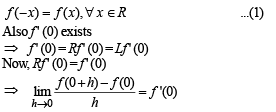
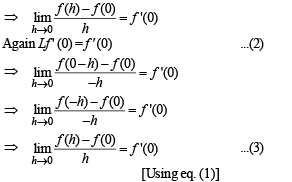
From equations (2) and (3), we get
⇒ f ' (0) = 0
Q.12. Find the values of a and b so that the function
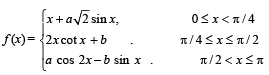
is continuous for 0 < x < π.
Ans.
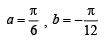
Solution. Given that,
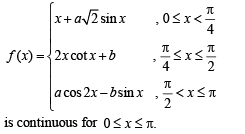
∴ f (x) must be continuous at 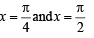
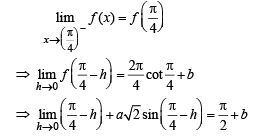
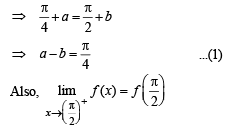

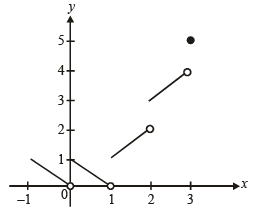
Q.13. Draw a graph of the function y = [x] + | 1 – x |, -1 < x < 3 . Determine the points, if any, where this function is not differentiable.
Ans. x = 0, 1, 2, 3
Solution. We have, [x] + | 1– x |, -1 < x < 3
NOTE THIS STEP
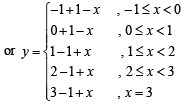
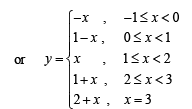
From graph we can say that given functions is not differentiable at x = 0, 1, 2, 3.
Q.14. 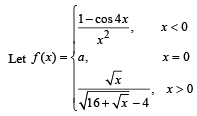
Determine the value of a, if possible, so that the function is continuous at x = 0
Ans. a = 8
Solution. We are given that,
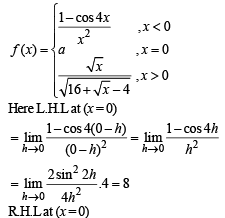
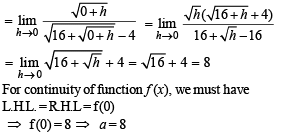
Q.15. A function f : R → R satisfies the equation f (x + y) = f (x) f (y) for all x, y in R and f (x) ≠ 0 for any x in R. Let the function be differentiable at x = 0 and f' (0) = 2. Show that f' (x) = 2 f (x) for all x in R. Hence, determine f (x).
Ans. f (x) = e2x
Solution. We are given
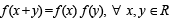
f (x ) ≠ 0, for any x
f is differentiable at x = 0, f ' (0) = 2
We have for x = y = 0
f (0 + 0) = f (0) f (0)
⇒ f (0) = [f (0)]2 ⇒ f (0) = 1
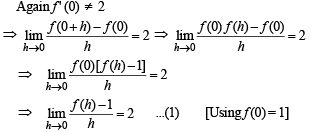

Integrating on both sides with respect to x, we get
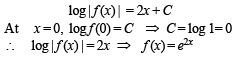
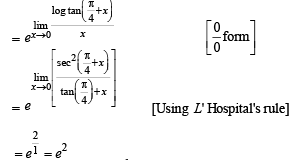
Q.16. 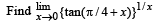
Ans. e2
Solution.
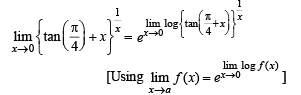
Q.17.
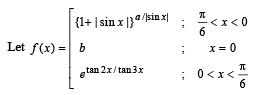
Determine a and b such that f(x) is continuous at x = 0
Ans. 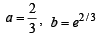
Solution.
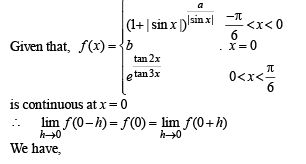
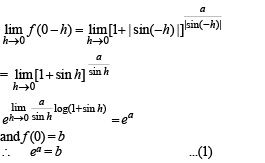
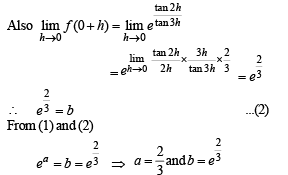
Q.18. 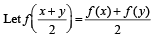 for all real x and y. If f '(0) exists and equals – 1 and f (0) =1, find f (2).
for all real x and y. If f '(0) exists and equals – 1 and f (0) =1, find f (2).
Ans. f(2) = –1
Solution.
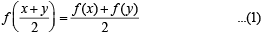
Putting y = 0 and f (0) = 1 in (1), we get
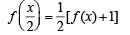
 ...(2)
...(2)
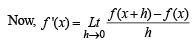
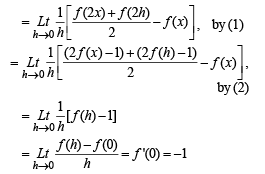
Hence f '(x) = – 1, integrating, we get
f (x) = – x + c. Putting x = 0, we get
f (0) = c = 1 by (1) ∴ f (x) = 1 – x
f (2) = 1 – 2 = – 1
Q.19. Determine the values of x for which the following function fails to be continuous or differentiable:
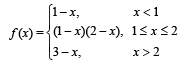 Justify your answer..
Justify your answer..
Ans. f is continuous and differentiable at all points except at x = 2.
Solution. By the given definition it is clear that the function f is continuous and differentiable at all points except possible at x = 1 and x = 2.
Continuity at x = 1
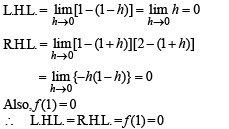
Therefore, f is continuous at x = 1
Now, differentiability at x = 1
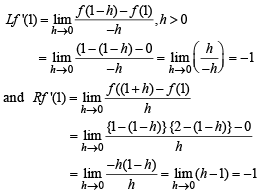
Since Lf ' (1) = Rf ' (1)
Hence, f is differentiable at x = 1
Continuous at x = 2
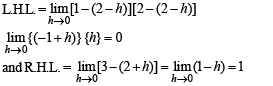
Since L.H.L.≠ R.H.L., therefore f is not continuous at x = 2. As such f cannot be differentiable at x = 2. Hence f is continuous and differentiable at all points except at x = 2.
Q. 20. Let f (x), x > 0, be a non-negative continuous function, and 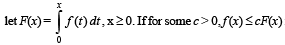 for all x > 0, then show that f(x) = 0 for all x > 0.
for all x > 0, then show that f(x) = 0 for all x > 0.
Solution. Given that,
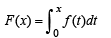
NOTE THIS STEP
∴ F ' (x) = f (x).1– f (0).0
[Using Leibnitz theorem]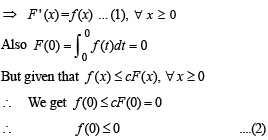
But ATQ f (x) is non- negative continuous function on [0, ∞)
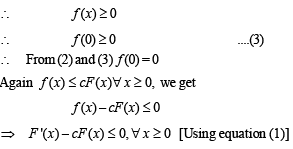
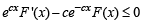
[Multiplying both sides by e–cx (I.F.) and keeping in
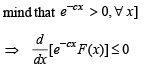
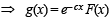 is a decreasing function on [0,∞).
is a decreasing function on [0,∞).

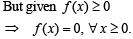
Q. 21. Let a ∈ R. Prove that a function f : R → R is differentiable at a if and only if there is a function g : R → R which is continuous at a and satisfies f(x) - f(a) = g(x) (x - a) for all x ∈ R.
Solution. (I) g is continuous at α and
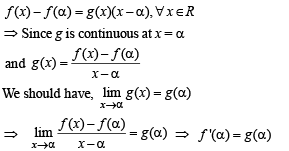
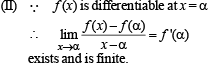
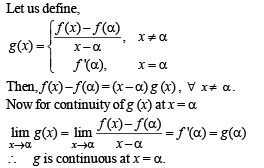
Q. 22. 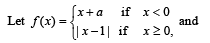
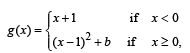 where a and b are non-negative real numbers. Determine the composite function g o f. If (g o f) (x) is continuous for all real x, determine the values of a and b. Further, for these values of a and b, is g o f differentiable at x = 0?
where a and b are non-negative real numbers. Determine the composite function g o f. If (g o f) (x) is continuous for all real x, determine the values of a and b. Further, for these values of a and b, is g o f differentiable at x = 0?
Ans. 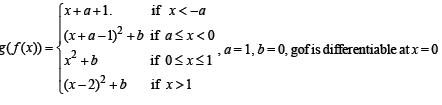
Solution. Given that
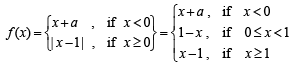
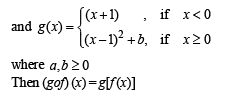
NOTE THIS STEP
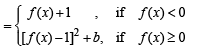
(Using definition of g(x)
Now, f (x) < 0 when x + a < 0 i.e. x < – a
f (x) = 0 when x = – a or x = 1
f (x) > 0 when – a < x < 1 or x > 1
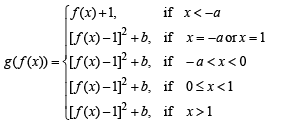
[Keeping in mind that x = 0 and 1 are also the breaking points because of definition of f (x)]
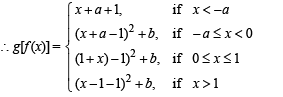
Substituting the value of f (x) under different conditions).
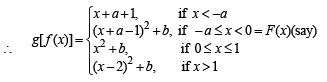
Now given that gof (x) ≡ F (x) is continuous for all real numbers, therefore it will be continuous at – a
⇒ L.H.S = R.H.L = f (– a)
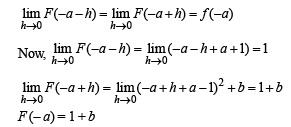
Thus we should have 1 = 1 + b ⇒ b = 0.
Again for continuity at x = 0
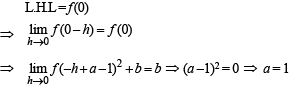
For a = 1 and b = 0, gof becomes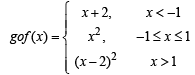
Now to check differentiability of gof (x) at x = 0 We see, gof (x) = x2 = F(x)
⇒ F ' (x) = 2x which exists clearly at x = 0. gof is differentiable at x = 0
Q. 23. If a f unction f : [-2a, 2a]→R is an odd function such that f(x) = f(2a – x) for x ∈[a, 2a] and the left hand derivative at x = a is 0 then find the left hand derivative at x = – a.
Ans. 0
Solution. Given that f : [– 2a, 2a ] → R
f is an odd function.
Lf ' at x = a is 0.
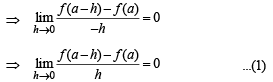
To find Lf ' at x = – a which is given by
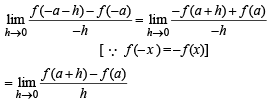
Substiting this values in last expression we get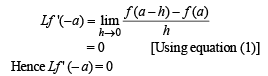
Q. 24. 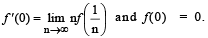 Using this find
Using this find
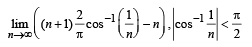
Ans. 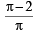
Solution. To find,
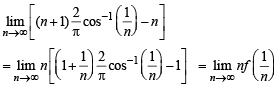
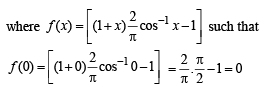
∴ Using given relation as 
then given limit becomes
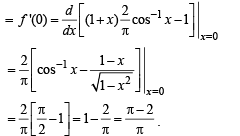
Q. 25. 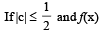 and f(x) is a differentiable function at x = 0 given
and f(x) is a differentiable function at x = 0 given
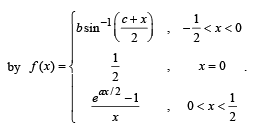
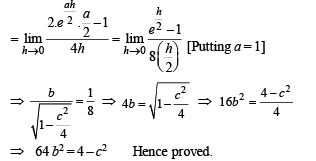
Find the value of ‘a’ and prove that 64 b2 = 4 – c2
Ans. 1
Solution. Given that, f (x) is differentiable at x = 0.
Hence, f (x) will also be continuous at x = 0
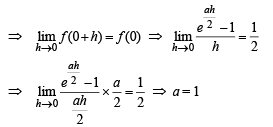
Also differentiability of f (x) at x = 0, gives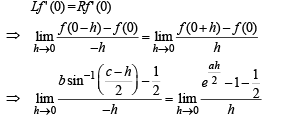
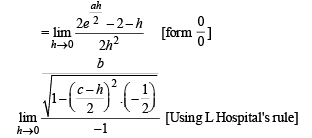
Q. 26. If f (x - y) = f (x) ×g (y) - f (y)×g (x) and g (x -y) = g (x) × g (y)- f (x)×f (y) for all x, y ∈ R . If right hand derivative at x = 0 exists for f(x). Find derivative of g(x) at x = 0
Ans. 0
Solution. Given that,
f (x – y) = f (x). g (y) – f (y) . g (x) ...(i)
g (x – y) = g (x). g (y) + f (x) f (y) ...(ii)
In eqn. (i), putting x = y, we get
f (0) = f (x) g (x) – f (x) g (x) Þ f (0) = 0
Putting y = 0, in eqn. (i), we get
f (x) = f (x) g (0) – f (0) g (x)
⇒ f (x) = f (x) g (0) [using f (0) = 0]
⇒ g (0) = 1
Putting x = y in eqn. (ii), we get
g (0) = g (x) g (x) + f (x) f (x)
⇒ 1 = [g (x)]2 + [f (x)]2 [using g (0) = 1]
⇒ [g (x)]2 = 1 – [f (x)]2 ...(iii)
learly g (x) will be differentiable only if f (x) is differentiable.
∴ First we will check the differentiability of f (x) Given that Rf ' (0) exists
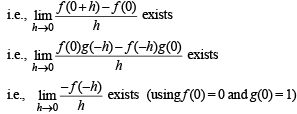
Which can be written as,
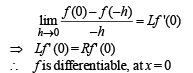
Differentiating equation (iii), we get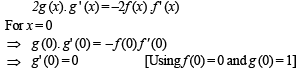
|
446 docs|929 tests
|





















