Subjective Type Questions: Functions | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Q. 1. Find the domain and range of the function 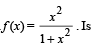 the function one-to-one?
the function one-to-one?
Solution. Since f (x) is defined and real for all real values of x, therefore domain of f is R.
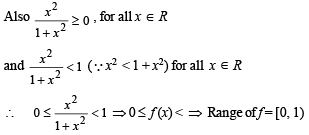
Also since f (1) = f (–1) = 1/2
∴ f is not one-to-one.
Q. 2. Draw the graph of y = | x |1/2 for – 1 < x < 1.
Solution.
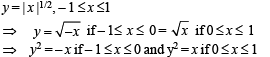
[Here y should be taken always + ve, as by definition y is a + ve square root].
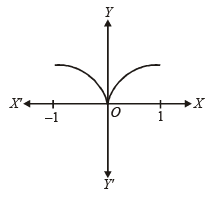
Clearly y2 = – x represents upper half of left handed parabola (upper half as y is + ve) and y2 = x represents upper half of right handed parabola.
Therefore the resulting graph is as shown below :
Q. 3. If f (x) = x9 – 6x8 – 2x7 + 12x6 + x4 – 7x3 + 6x2 + x – 3, find f (6).
Solution. f (x) = x9 – 6x8 – 2x7 + 12x6 + x4 – 7x3 + 6x2 + x – 3
Then f (6) = 69 – 6 × 68 – 2 × 67 + 12 × 66 + 64 – 7 × 63 + 6 × 62 + 6 – 3
= 69 – 69 – 2 × 67 + 2 × 67 + 64 – 7 × 63 + 63 + 6 – 3 = 3
Q. 4. Consider the following relations in the set of real numbers R.
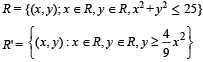
Find the domain and range of R ∩ R'. Is the relation R ∩ R' a function?
Solution. R = [(x, y); x ∈ R, y ∈ R, x2 + y2 < 25] which represents all the points inside and on the circle x2 + y2 = 52, with centre (0, 0) and radius = 5
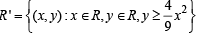
which represents all the points inside and on the upward parabola 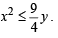
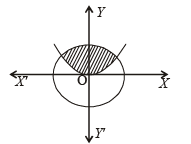
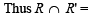
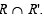 = The set of all points in shaded region.
= The set of all points in shaded region.
For
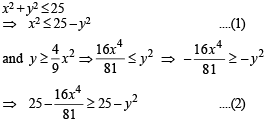
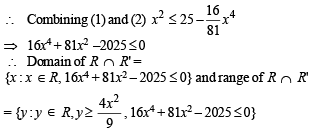
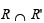 is not a function because image of an element is not unique , e..g., (0, 1), (0, 2), (0,3) .....
is not a function because image of an element is not unique , e..g., (0, 1), (0, 2), (0,3) ..... 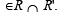
Q. 5. Let A and B be two sets each with a finite number of elements. Assume that there is an injective mapping from A to B and that there is an injective mapping from B to A. Prove that there is a bijective mapping from A to B.
Solution. As there is an injective maping from A to B, each element of A has unique image in B. Similarly as there is an injective mapping from B to A, each element of B has unique image in A. So we can conclude that each element of A has unique image in B and each element of B has unique image in A or in other words there is one to one mapping from A to B. Thus there is bijective mapping from A to B.
Q.6. Let f be a one-one function with domain {x, y, z} and range {1, 2, 3}. It is given that exactly one of the following statements is true and the remaining two are false f (x) = 1, f (y) ≠ 1, f (z ) ≠ 2 determine f–1(1).
Solution. f is one one function,
Df = {x, y, z}; Rf = {1, 2, 3}
Eaxctly one of the following is true :
f (x) = 1, f (y) ≠ 1, f (z) ≠ 2
To determine f –1 (1):
Case I: f (x) = 1 is tr ue.
⇒ f (y) ≠ 1, f (z) ≠ 2 are false.
⇒ f (y) = 1, f (z) = 2 are true.
But f (x) = 1, f (y) = 1 are true, is not possible as f is one to one.
∴ This case is not possible.
Case II: f (y) ≠ 1 is true.
⇒ f (x) = 1 and f (z) ≠ 2 are false
⇒ f (x) ≠1 and f (z) = 2 are true
Thus, f (x) ≠ 1, f (y) ≠ 1, f (z) = 2
⇒ Either f (x) or f (y) = 2. So, f is not one to one
∴ This case is also not possible.
∴ f (z) ≠ 2 is true
∴ f (x) = 1 and f (y) ≠ 1 are false.
⇒ f (x) ≠ 1 and f (y) = 1 are true.
⇒ f –1 (1) = y
Q.7. Let R be the set of real numbers and f : R → R be such that for all x and y in R |f (x) – f(y) | < | x – y |3 . Prove that f(x) is a constant
Solution.
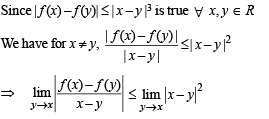
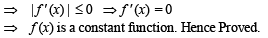
Q.8. Find the natural number ‘a’ for which 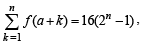 where the function ‘f’ satisfies the relation f(x + y) = f (x) f (y) for all natural numbers x, y and further f(1) = 2.
where the function ‘f’ satisfies the relation f(x + y) = f (x) f (y) for all natural numbers x, y and further f(1) = 2.
Solution. Given that 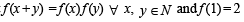
To find ‘a’ such that,
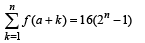 ...(1)
...(1)
For this we start with ...(2)
f (1) = 2
Then f (2) = f (1 + 1) = f (1) f (1)
⇒ f (2) = 22
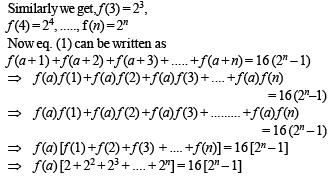
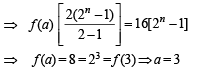
Q.9. Let {x} and [x] denotes the fractional and integral part of a real number x respectively. Solve 4{x} = x + [x].
Solution. Given that 4 {x} = x + [x]
Where [x] = greatest integer < x
{x} = fractional part of x
∴ x = [x] + {x} for any x ∈ R
∴ Given eqn becomes
4 {x} = [x] + {x} + [x] ⇒ 3 {x} = 2 [x]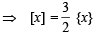 ....(1)
....(1)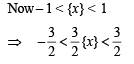
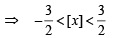 [Using eqn (1)]
[Using eqn (1)]
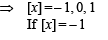
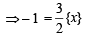 [Using eqn (1)]
[Using eqn (1)]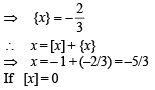
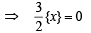 [Using eqn (1)]
[Using eqn (1)]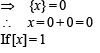
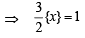 [Using eqn (1)]
[Using eqn (1)]
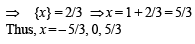
Q.10. A function f :IR → IR, where IR is the set of real numbers, is defined by 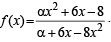 Find the interval of values of α for which f is onto. Is the function one-to-one for α = 3?
Find the interval of values of α for which f is onto. Is the function one-to-one for α = 3?
Solution.
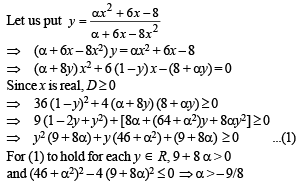
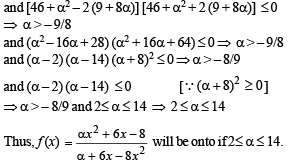
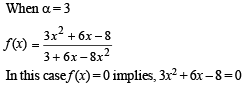
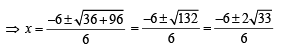
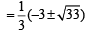
This shows that
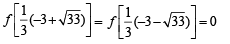
Therefore, f is not one-to-one at α = 3.
Q.11. Let f(x) = Ax2 + Bx +C where A, B, C are real numbers. Prove that if f(x) is an integer whenever x is an integer, then the numbers 2A, A + B and C are all integers. Conversely, prove that if the numbers 2A, A+B and C are all integers then f(x) is an integer whenever x is an integer.
Solution. Suppose f (x) = Ax2 + Bx + C is an integer whenever x is an integer.
∴ f (0), f (1), f (–1) are integers
⇒ C, A + B + C, A – B + C are integers.
⇒ C, A + B, A – B are integers
⇒ C, A + B, (A + B) + (A – B) = 2A are integers.
Conversely suppose 2A, A + B and C are integers.
Let x be any integer.
We have
f (x) = Ax2 + Bx + C
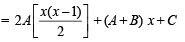
Since x is an integer x, x (x – 1)/2 is an integer.
Also 2A, A + B and C are integers.
We get f (x) is an integer for all integer x.
|
347 docs|185 tests
|
FAQs on Subjective Type Questions: Functions - JEE Advanced - 35 Years Chapter wise Previous Year Solved Papers for JEE
| 1. What are functions in JEE Advanced? |  |
| 2. How are functions represented in JEE Advanced? |  |
| 3. What is the importance of functions in JEE Advanced? |  |
| 4. How are functions evaluated in JEE Advanced? |  |
| 5. Can functions in JEE Advanced be composed or combined? |  |





















