JEE Advanced (Subjective Type Questions): Moving Charges & Magnetism | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. A bar magnet with poles 25 cm apart and of strength 14.4 amp-m rests with centre on a frictionless pivot. It is held in equilibrium at an angle of 60° with respect to a uniform magnetic field of induction 0.25 Wb/m2, by applying a force F at right angles to its axis at a point 12 cm from pivot.Calculate F. What will happen if the force F is removed?
Ans. 25.98 N
Solution. 2l = 0.25 m
Also, m × 2l = 14.4 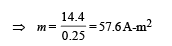
Torque due to magnetic field
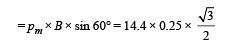
The torque due to the force = F × 0.12
For equilibrium F × 0.12 = 14.4 × 0.25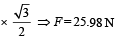
If the force F is removed, the torque due to magnetic field will move the bar magnet. It will start oscillating about the mean position where the angle between  and
and 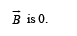
Q.2. A bar magnet is placed with its north pole pointing north and its south pole pointing south. Draw a figure to show the location of neutral points.
Solution.
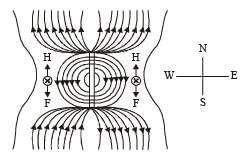
Q.3. A potential difference of 600 volts is applied across the plates of a parallel plate condenser. The separation between the plates is 3 mm. An electron projected vertically, parallel to the plates, with a velocity of 2 × 106 m/sec moves undeflected between the plates. Find the magnitude and direction of the magnetic field in the region between the condenser plates. (Neglect the edge effects). (Charge of the electron = – 1.6 × 10–19 coulomb)
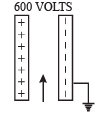
Ans. 0.1T, Directed perpendicular to the plane of paper inwards.
Solution. The force on electron will be towards the left plate due to electric field and will be equal to Fe = eE
NOTE : For the electron to move undeflected between the plates there should be a force (magnetic) which is equal to the electric force and opposite in direction. The force should be directed towards the right as the electric force is towards the left.
On applying Fleming's left hand rule we find the magnetic field should be directed perpendicular to the plane of paper inwards. Therefore, Force due to electric field = Force due to magnetic field. eE = evB

where V = p.d. between plates
d = distance between plates
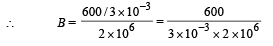
B = 0.1 tesla
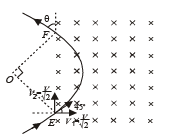
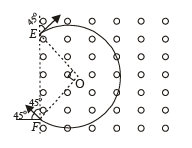
Q.4. A particle of mass m = 1.6 × 10–27 kg and charge q = 1.6 × 10–19 C enters a region of uniform magnetic field of strength 1 tesla along the direction shown in fig. The speed of the particle is 107 m/ s. (i) The magnetic field is directed along the inward normal to the plane of the paper. The particle leaves the region of the field at the point F. Find the distance EF and the angle θ. (ii) If the direction of the field is along the outward normal to the plane of the paper, find the time spent by the particle in the region of the magnetic field after entering it at E.
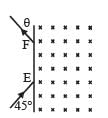
Ans. (i) 0.1414 m, 45° (ii) 4.71 × 10–8 sec.
Solution.
m = 1.6 × 10–27 kg, q = 1.6 × 10–19 C
B = 1 T
v = 107 m/s
F = q . v B sin α
(acting towards O by Fleming's left hand rule)
⇒ F = qvB [∴α = 90°]
But F = ma
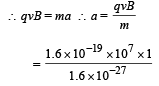
= 1015 m/s2
∠ OEF = 45° (∴ OE act as a radius)
By symmetry ∠ OEF = 45°
∴ ∠EOF = 90° (by Geometry)
This is the centripetal acceleration
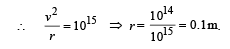
Therefore EF = 0.141 m.
If the magnetic field is in the outward direction and the particle enters in the same way at E, then according to Fleming's left hand rule, the particle will turn towards clockwise direction and cover 3/4th of a circle as shown in the figure.
Q.5. A beam of protons with a velocity 4 × 105 m/sec enters a uniform magnetic field of 0.3 tesla at an angle of 60° to the magnetic field. Find the radius of the helical path taken by the proton beam. Also find the pitch of the helix (which is the distance travelled by a proton in the beam parallel to the magnetic field during one period of rotation).
Ans. 0.012 m, 0.044 m
Solution.
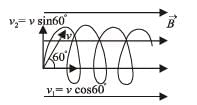
v1 is responsible for horizontal motion of proton
v2 is responsible for circular motion of proton
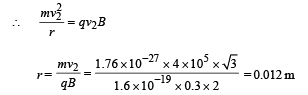
Pitch of helix = v1 × T
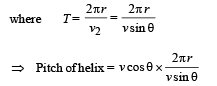
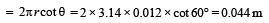
Q.6. Two long straight parallel wires are 2 metres apart, perpendicular to the plane of the paper (see figure). The wire A carries a current of 9.6 amps, directed into the plane of the paper.The wire B carries a current such that the magnetic field of induction at the point P, at a distance of 10/11 metre from the wire B, is zero.
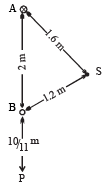
Find :
(i) The magnitude and direction of the current in B .
(ii) The magnitude of the magnetic field of induction at the point S.
(iii) The force per unit length on the wire B.
Ans. (i) 3A, upward direction (ii) 1.3 × 10–6 T (iii) 28.8 × 10–7 N
Solution. (i) The magnetic field at P due to current in wire A.
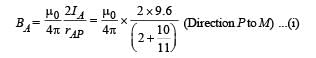
NOTE : The current in wire B should be in upward direction so as to cancel the magnetic field due to A at P. (By right hand Thumb rule)
The magnetic field at P due to current in wire B
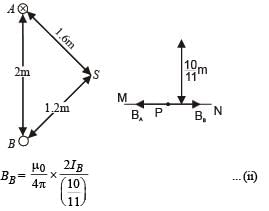
From (i) and (ii)
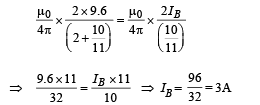
(ii) The dimensions given shows that
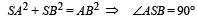
Magnetic field due to A at S
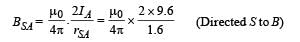
Magnetic field due to B at S
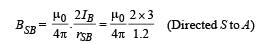
The resultant magnetic field
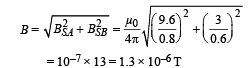
(iii) Force per unit length on wire B
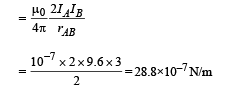
This force will be repulsive in nature.
Q.7. A pair of stationary and infinitely long bent wires are placed in the XY plane as shown in fig. The wires carry currents of i = 10 amperes each as shown. The segments L and M are along the X-axis. The segments P and Q are parallel to the Yaxis such that OS = OR = 0.02 m. Find the magnitude and direction of the magnetic induction at the origin O.
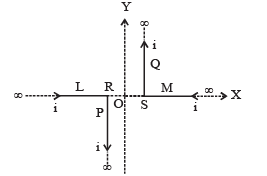
Ans. 10–4 tesla; directed towards the reader perpendicular to the plane of paper.
Solution.
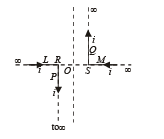
∴ Magnetic field due to current carrying conductor P at point O is
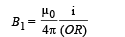
directed towards the reader perpendicular to the plane of paper.
Magnetic field due to current carrying conductor Q at point O is directed towards the reader perpendicular to the plane of paper.
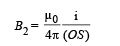
Magnetic field due to current carrying conductors L and M at O is zero.
∴ Resultant magnetic field at O
B = B1 + B2
(directed towards the reader perpendicular to the plane of paper)
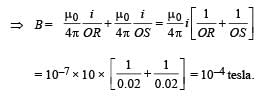
Q.8. Two long parallel wires carrying current 2.5 amperes and I ampere in the same direction (directed into the plane of the paper ) are held at P and Q respectively such that they are perpendicular to the plane of paper. The points P and Q are located at a distance of 5 metres and 2 metres respectively from a collinear point R (see figure)
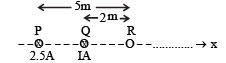
(i) An electron moving with a velocity of 4 × 105 m/s along the positive x - direction experiences a force of magnitude 3.2 × 10–20 N at the point R. Find the value of I.
(ii) Find all the positions at which a third long parallel wire carrying a current of magnitude 2.5 amperes may be placed so that the magnetic induction at R is zero.
Ans. (i) 4 A. (ii) r = 1m where r is the distance from R
Solution. The magnetic field (due to current in wire P) at R
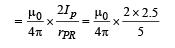
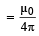 [in the plane of paper downwards]
[in the plane of paper downwards]
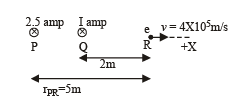
Similarly, the magnetic field (due to current is wire Q) at R
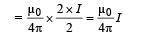
[in the plane of paper downwards]
The total magnetic field at R [due to P and Q]
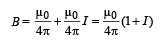
[in the plane of paper downwards]
The force experienced by the electron
F = qvBsinθ
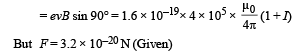
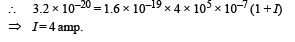
(ii) Let us consider a position between Q and R. The magnetic field produced should be equal to 5 × 10–7 T in the plane of paper acting upwards.
For this let the wire having current 2.5 amp be placed at a distance r from R and current flowing outwards the plane of paper.
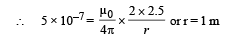
Let us consider another position beyond R collinear with P, Q and R. Let it be placed at a distance r' from R, having current in the plane of paper.
Q.9. A wire loop carrying a current I is placed in the x-y plane as shown in fig.
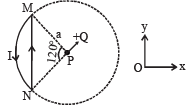
(a) If a particle with charge +Q and mass m is placed at the centre P and given a velocity 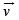 along NP (see figure), find its instantaneous acceleration.
along NP (see figure), find its instantaneous acceleration.
(b) If an external uniform magnetic in duction field 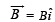 is applied, find the force and the torque acting on the loop due to this field.
is applied, find the force and the torque acting on the loop due to this field.
Ans.(a) directed 30° with the negative X-axis (b) zero, 0.614
Solution.
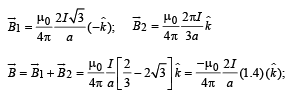
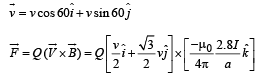
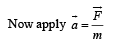
(b) KEY CONCEPT : The torque acting on the loop in the magnetic field is given by

A = (area of PMQNP) – (area of triangle PMN)
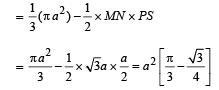
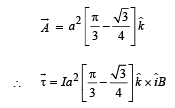
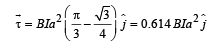
The force acting on the loop is zero.
Q.10. A straight segment OC (of length L meter) of a circuit carrying a current I amp is placed along the x-axis (Fig.). Two infinetely long straight wires A and B, each extending from z = - ∞ to +∞ , are fixed at y = – a meter and y = + a meter respectively,, as shown in the figure.
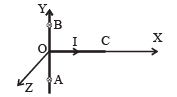
If the wires A and B each carry a current I amp into the plane of the paper, obtain the expression for the force acting on the segment OC. What will be the force on OC if the current in the wire B is reversed ?
Ans. directed toward –Z direction, zero.
Solution. The magnetic field produced at different points on OC will be different. Let us consider an arbitrary point P on OC which is at a distance x from the origin. Let the magnetic field due to currents in A and B at P be B1 and B2 respectively, both being in the X-Y plane.
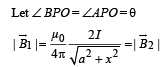
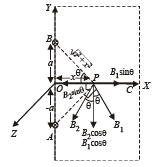
On resolving B1 and B2 we get xq B1sinc that the sin q components cancel out and the cos q components add up.
Therefore, the total magnetic field at P is
B = 2B1 cos θ
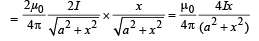
(towards – Y direction) Let us consider a small portion of wire OC at P of length dx.
The small amount of force acting on that small portion
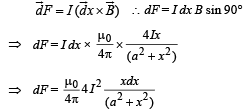
The total force
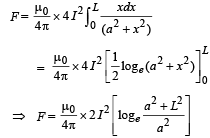
To find the direction of force we can use Fleming's left hand rule. The direction of 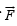 is towards – Z direction.
is towards – Z direction.
When the current in wire B is reversed, the resultant magnetic field at any arbitrary point P on OC will be in the X-direction. Since the current is also in X-direction, therefore force acting will be zero (F = I lB sin θ and θ = 180°).
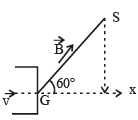
Q.11. An electron gun G emits electrons of energy 2keV travelling in the positive x-direction. The electrons are required to hit the spot S where GS = 0.1m, and the line GS makes an angle of 60° with the x-axis as shown in the fig. A uniform magnetic field 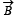 parallel to GS exists. Find
parallel to GS exists. Find 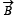 parallel to GS exists in the region outside the electron gun. Find the minimum value of B needed to make the electrons hit S.
parallel to GS exists in the region outside the electron gun. Find the minimum value of B needed to make the electrons hit S.
Ans. 4.737 × 10–3 T
Solution. (a) Let us resolve the velocity into two rectangular components v1 (= vcos 60°) and v2 (= vsin 60°). v1 component of velocity is responsible to move the charge particle in the direction of the magnetic field whereas v2 component is responsible for revolving the charged particle in circular motion. The overall path is helical. The condition for the charged particle to strike S with minimum value of B is that Pitch of Helix = GS
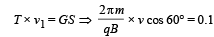
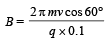
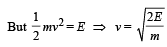
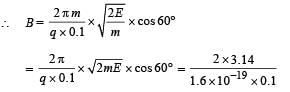
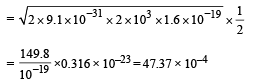
= 4.737 × 10–3 T
Q.12. A long horizontal wire AB, which is free to move in a vertical plane and carries a steady current of 20A, is in equilibrium at a height of 0.01 m over another parallel long wire CD which is fixed in a horizontal plane and carries a steady current of 30A, as shown in figure . Show that when AB is slightly depressed, it executes simple harmonic motion. Find the period of oscillations.

Ans. 0.2 sec.
Solution. When AB is steady,
Weight per unit length = Force per unit length
Weight per unit length = 
NOTE : When the rod is depressed by a distance x, then the force acting on the upper wire increases and behaves as a restoring force
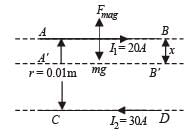
Restoring force/length = 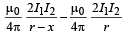
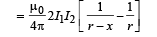
⇒ Restoring force/length = 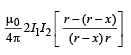
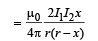
When x is small i.e., x 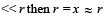
Restoring force/length F = 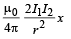
Since, F ∝ x and directed to equilibrium position.
∴ The motion is simple harmonic
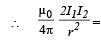 (mass per unit length) ω2 ... (ii)
(mass per unit length) ω2 ... (ii)
From (i), (Mass per unit length) × g =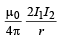
Mass per unit length =
From (ii) and (iii)
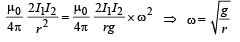
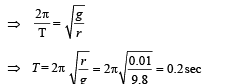
Q.13. An electron in the ground state of hydrogen atom is revolving in anticlock-wise direction in a circular orbit of radius R.
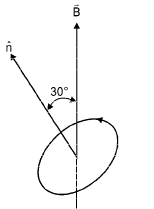
(i) Obtain an expression for the orbital magnetic dipole moment of the electron.
(ii) The atom is placed in a uniform magnetic induction 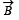 such that the plane-normal of the electron-orbit makes an angle of 30° with the magnetic induction. Find the torque experienced by the orbiting electron.
such that the plane-normal of the electron-orbit makes an angle of 30° with the magnetic induction. Find the torque experienced by the orbiting electron.
Ans. directed perpendicular to the plane containing
Solution. (i) KEY CONCEPT : Orbital magnetic dipole moment M = IA where I is the current due to orbital motion of electron and A is the area of loop made by electron.
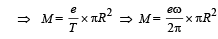
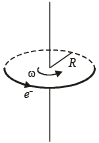
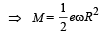
But according to Bohr's postulate
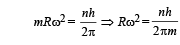
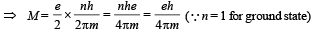
NOTE : The direction of magnetic momentum is same as the direction of area vector, i.e., perpendicular to the plane of orbital motion.
(ii) KEY CONCEPT : We know that torque
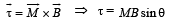
where θ is the angle between M and B
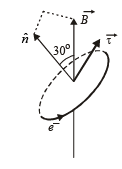
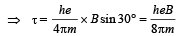
NOTE : The direction of torque can be found by right hand thumb rule.
The direction of torque is perpendicular to the plane containing 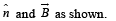
Q.14. Three infinitely long thin wires, each carrying current i in the same direction, are in the x-y plane of a gravity free space. The central wire is along the y-axis while the other two are along x = ± d.
(i) Find the locus of the points for which the magnetic field B is zero.
(ii) If the central wire is displaced along the Z-direction by a small amount and released, show that it will execute simple harmonic motion. If the linear density of the wires is λ, find the frequency of oscillation.
Ans.
Solution. (i) KEY CONCEPT : Magnetic field due to an infinitely long current carrying wire at distance r is given by
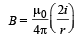
The direction of B is given by right hand palm rule.
Hence, in case of three identical wires, resultant field can be zero only if the point P is between the two wires, otherwise field B due to all the wires will be in the same direction and so resultant B cannot be zero. Hence, if point P is at a distance x from the central wire as shown in figure, then,
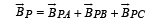
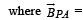 magnetic field at P due to A
magnetic field at P due to A
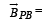 Magnetic field at P due to B
Magnetic field at P due to B
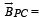 Magnetic field at P due to C.
Magnetic field at P due to C.
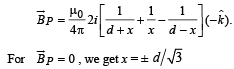
(ii) KEY CONCEPT : The force per unit length between two parallel current carrying wires is given by
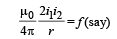
and is attractive if currents are in the same direction.
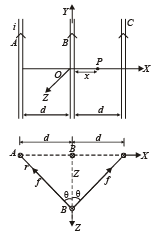
So, when the wire B is displaced along Z-axis by a small distance Z, the restoring force per unit length F/l on the wire B due to wires A and C will be
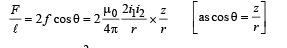
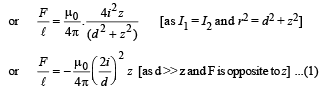
Since F ∝ – z, the motion is simple harmonic.
Comparing eq. (1) with the standard equation of S.H.M. which is
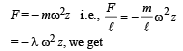
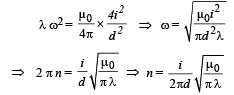
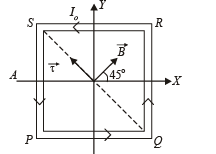
Q.15.A uniform, constant magnetic field B is directed y at an angle of 45° to the x axis in the xy-plane. PQRS is a rigid, square wire frame carrying a steady current I0, with its centre at the origin O. At time t = 0, the frame is at rest in the position as shown in Figure, with its sides parallel to the x and y axes. Each side of the frame is of mass M and length L.
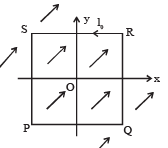
(a) What is the torque τ about O acting on the frame due to the magnetic field?
(b) Find the angle by which the frame rotates under the action of this torque in a short interval of time Δt, and the axis about this rotation occurs. (Δt is so short that any variation in the torque during this interval may be neglected.) Given : the moment of inertia of the frame about an axis through its centre perpendicular to its plane is 4/3 ML2.
Ans.
Solution. (a) As the magnetic field  is in x – y plane and subtends an angle of 45° with the x-axis, hence,
is in x – y plane and subtends an angle of 45° with the x-axis, hence,
Bx = B cos 45° = B /√2 and
By = B sin 45° = B /√2
So, in vector from
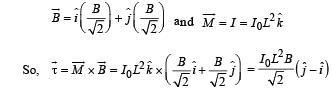
i.e., torque has magnitude I02L2B and is directed along line QS from Q to S.
(b) According to th e theorem of perpendicular axes, moment of inertia of the frame about QS.
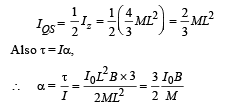
Here α is constant, therefore we can apply
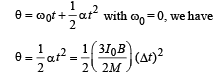
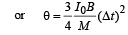
Q.16. The region between x = 0 and x = L is filled with uniform, steady magnetic field 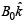 . A particle of mass m, positive charge q and velocity
. A particle of mass m, positive charge q and velocity 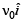 travels along x-axis and enters the region of the magnetic field. Neglect gravity throughout the question.
travels along x-axis and enters the region of the magnetic field. Neglect gravity throughout the question.
(a) Find the value of L if the particle emerges from the region of magnetic field with its final velocity at angle 30° to its initial velocity.
(b) Find the final velocity of the particle and the time spent by it in the magnetic field, if the magnetic field now extends up to 2.1L.
Ans.
Solution. KEY CONCEPT : This question involves a simple understanding of the motion of charged particle in a magnetic field.
(a)
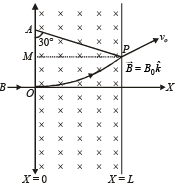
Let the particle emerge out from the region of magnetic field at point P. Then the velocity vector 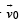 makes an angle 30° with x-axis. The normal to circular path at P intersects the negative y-axis at point A.
makes an angle 30° with x-axis. The normal to circular path at P intersects the negative y-axis at point A.
Hence, AO = AP = R = radius of circular path, which can be found as
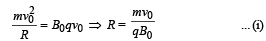
In ΔAPM, R sin 30° = L 
From (i) and (ii), L =mv0/2qB0
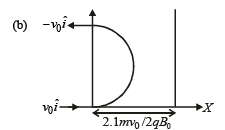
As the new region of magnetic field is 2.1 L
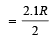 which is obviously > R.
which is obviously > R.
Thus, the required velocity =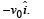
Since the time period for complete revolution = 2πm/qB0.
The time taken by the particle to cross the region of magnetic field = πm/qB0.
Q.17. A circular loop of radius R is bent along a diameter and given a shape as shown in the figure. One of the semicircles (KNM) lies in the x-z plane and the other one (KLM) in the yz plane with their centres at the origin. Current I is flowing through each of the semi circles as shown in figure.
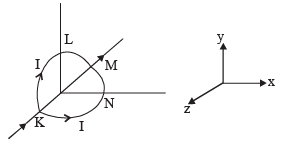
(a) A particle of charge q is released at the origin with a velocity 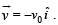 Find the instantaneous force
Find the instantaneous force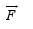 on the particle. Assume that space is gravity free.
on the particle. Assume that space is gravity free.
(b) If an external uniform magnetic field 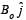 is applied, determine the force
is applied, determine the force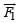 and
and 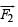 on the semicircles KLM and KNM due to the field and the net force
on the semicircles KLM and KNM due to the field and the net force 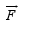 on the loop.
on the loop.
Ans.
Solution. (a) Magnetic field 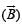 at the origin = Magnetic field due to semicircle KLM + Magnetic field due to other semicircle KNM.
at the origin = Magnetic field due to semicircle KLM + Magnetic field due to other semicircle KNM.
Therefore, 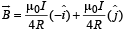
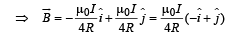
[NOTE : The magnetic field 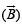 due to a circular current
due to a circular current
carrying loop is 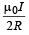 ∴For semicircle it is half]
∴For semicircle it is half]
Therefore, magnetic force acting on the particle.
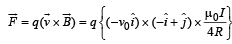
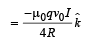
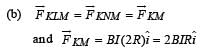
Therefore, 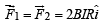 or total force on the loop,
or total force on the loop,
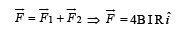
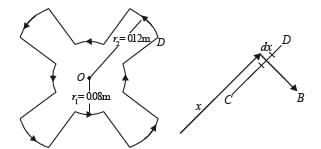
Q.18. A current of 10 A flows around a closed path in a circuit which is in the horizontal plane as shown in the figure. The circuit consists of eight alternating arcs of radii r1 = 0.08 m and r1 = 0.12 m. Each arc subtends the same angle at the center.
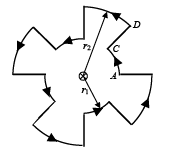
(a) Find the magnetic field produced by this circuit at the center.
(b) An infinitely long straight wire carrying a current of 10 A is passing through the center of the above circuit vertically with the direction of the current being into the plane of the circuit. What is the force acting on the wire at the center due to the current in the circuit?
What is the force acting on the arc AC and the straight segment CD due to the current at the center?
Ans. (a) 6.54 × 10–5T (b) 0, Force on arc AC = 0, 8.1 × 10–6N
Solution. For finding the magnetic field produced by this circuit at the centre we can consider it to contain two semicircles of radii, r1 = 0.08 m and r2 = 0.12 m. Since current is flowing in the same direction, the magnetic field created by circular arcs will be in the same direction and therefore will be added.
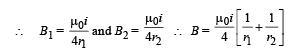
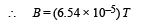 Directed outwards. (Right hand thumb rule)
Directed outwards. (Right hand thumb rule)
(b) Force acting on a current carrying conductor placed in a magnetic field is given by
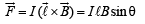
(i) For force acting on the wire at the centre In this case θ = 180°
∴ F = 0
(ii) On arc AC due to current at the centre
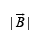 on AC will be B =
on AC will be B = 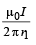
The direction of this magnetic field on any small segment of AC will be tangential
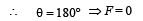
(iii) On segment CD.
Force on a small segment dx distant r from O
dF = I dxB
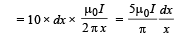
On integrating
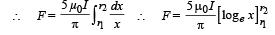
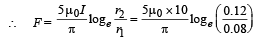
= 8.1 × 10–6 N
directed downwards (By Fleming left hand rule).
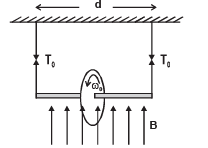
Q.19. A wheel of radius R having charge Q, uniformly distributed on the rim of the wheel is free to rotate about a light horizontal rod. The rod is suspended by light inextensible strings and a magnetic field B is applied as shown in the figure. The initial tensions in the strings are T0. If the breaking tension of the strings are 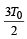 find the maximum angular velocity ω0 with which the wheel can be rotated.
find the maximum angular velocity ω0 with which the wheel can be rotated.
Ans.
Solution. When the ring is not rotating Wt. of ring = Tension in string mg = 2T0
∴ T0 =mg/2.... (i)
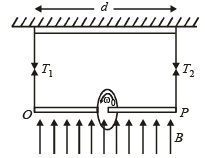
When the ring is rotating, we can treat it as a current carrying loop. The magnetic moment of this loop
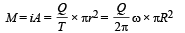
This current carrying loop will create its own magnetic field which will interact with the given vertical magnetic field in such a way that the tensions in the strings will become unequal. Let the tensions in the strings be T1 and T2.
For translational equilibrium
T1 + T2 = mg ... (ii)
Torque acting on the ring about the centre of ring
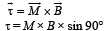
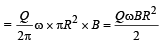
NOTE : For rotational equilibrium, the torque about the centre of ring should be zero.
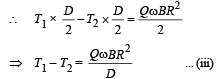
On solving (ii) and (iii), we get
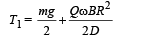
But the maximum tension is 3T0/2
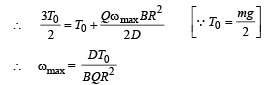
Q.20. A proton and an α-particle are accelerated with same potential difference and they enter in the region of constant magnetic field B perpendicular to the velocity of particles. Find the ratio of radius of curvature of proton to the radius of curvature of α - particle.
Ans. 1/√2
Solution. KEY CONCEPT :
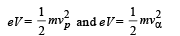
V is the potential difference
vp = velocity of proton
vα = velocity of α-particle
m = mass of proton, mass of a-particle = 4 m
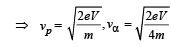
Now when the particles enter in magnetic field, the force on proton is
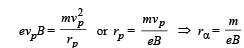
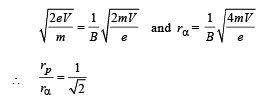
Q.21. In a moving coil galvanometer, torque on the coil can be expressed as τ= ki , where i is current through the wire and k is constant. The rectangular coil of the galvanometer having number of turns N, area A and moment of inertia I is placed in magnetic field B. Find
(a) k in terms of given parameters N, I, A and B
(b) the torsion constant of the spring, if a current i0 produces a deflection of π/2 in the coil.
(c) the maximum angle through which the coil is deflected, if charge Q is passed through the coil almost instantaneously. (ignore the damping in mechanical oscillations).
Ans. (a) k = NAB
Solution. (a) The torque acting on a rectangular coil placed in a uniform magnetic field is given by,
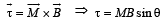
But M = N i A and θ = 90° (for moving coil galvanometer)
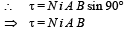
But τ = k i (given)
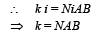
(b) The torsion constant is given by
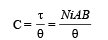
Here given that when i = i0, θ =π /2
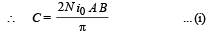
(c) We know that angular Impulse
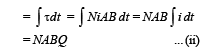
This angular impulse creates an angular momentum

From (ii) and (iii)
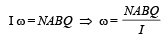
This is the instantaneous angular momentum due to which the coil starts rotating. Let us apply the law of energy conservation to find the angle of rotation.
Rotational kinetic energy of coil
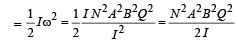
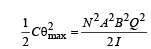
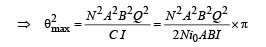
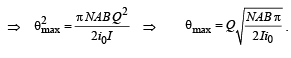
|
446 docs|929 tests
|
















