Subjective Type Questions: Probability - 1 | JEE Advanced | Question Bank for JEE Main & Advanced (350+ Tests) PDF Download
Q.1. Balls are drawn one-by-one without replacement from a box containing 2 black, 4 white and 3 red balls till all the balls are drawn. Find the probability that the balls drawn are in the order 2 black, 4 white and 3 red. (1978)
Ans. Sol. To draw 2 black, 4 white and 3 red balls in order is same as arranging two black balls at first 2 places, 4 white at next 4 places, (3rd to 6th place) and 3 red at still next 3 places (7th to 9th place), i.e., B1B2 W1W2W3W4R1 R2 R3, which can be done in 2! × 4! × 3! ways. And total ways of arranging all 2 + 4 + 3 = 9 balls is 9!
∴ Required probability = 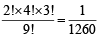
Q.2. Six boys and six gir ls sit in a row randomly. Find the probability that (i) the six girls sit together (ii) the boys and girls sit alternately. (1979)
Ans. Sol. (i) 6 boys and 6 girls sit in a row randomly.
Total ways of their seating = 12!
No. of ways in which all the 6 girls sit together = 6! × 7! (considering all 6 girls as one person)
∴ Probability of all girls sitting together
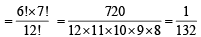
(ii) Staring with boy, boys can sit in 6! ways leaving one place between every two boys and one a last.
B _ B _ B _ B _ B_ B_
These left over places can be occupied by girls in 6! ways.
∴ If we start with boys. no. of ways of seating boys and girls alternately = 6!× 6!
In the similar manner, if we start with girl, no. of ways of seating boys and girls alternately = 6! × 6!
G _ G _ G _ G _ G_ G _
Thus total ways of alternate seating arrangements = 6! × 6! + 6! × 6!
= 2 × 6! × 6!
∴ Probability of making alternate seating arrangement for 6 boys and 6 girls
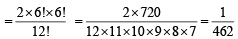
Q.3. An anti -aircraft gun can take a maximum of four shots at an enemy plane moving away from it.The probabilities of hitting the plane at the first, second, third and fourth shot are 0.4, 0.3, 0.2 and 0.1 respectively. What is the probability that the gun hits the plane ? (1981 - 2 Marks)
Ans. Sol. (a) Let us define the events as :
E1 ≡ First shot hits the target plane,
E2 ≡ Second shot hits the target plane
E3 ≡ third shot hits the target plane,
E4 ≡ fourth shot hits the target plane then
ATQ, P (E1) = 0.4; P (E2) = 0.3; P (E3) = 0.2; P (E4) = 0.1
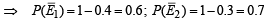
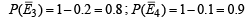
(where 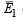 denotes not happening of E1)Now the gun hits the plane if at least one of the four shots hit the plane.
denotes not happening of E1)Now the gun hits the plane if at least one of the four shots hit the plane.
Also, P (at least one shot hits the plane).
= 1– P (none of the shots hits the plane)
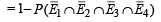

[Using multiplication thm for independent events] = 1– 0.6 × 0.7 × 0.8 × 0.9 = 1– 0.3024 = 0.6976
Q.4. A and B are two candidates seeking admission in IIT. The probability that A is selected is 0.5 and the probability that both A and B are selected is atmost 0.3. Is it possible that the probability of B getting selected is 0.9 ? (1982 - 2 Marks)
Ans. Sol. Let A denote the event that the candidate A is selected and B the event that B is selected. It is given that P (A) = 0.5 … (1)
P (A ∩ B ) ≤ 0.3 … (2)
Now, P (A) + P (B) – P (A ∩ B) = P (A ∪ B) ≤ 1 or 0.5 + P (B) – P (A ∩ B) < 1 [Using (1)]
or P (B) ≤ 0.5 + P (A ∩ B) ≤ 0.5 + 0.3 [Using (2)] or P (B) ≤ 0.8
∴P (B) can not be 0.9.
Q.5. Cards are drawn one by one at random from a well -shuffled full pack of 52 playing cards until 2 aces are obtained for the first time. If N is the number of cards required to be drawn, then show that 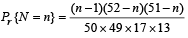 where 2 ≤ n ≤ 50 (1983 - 3 Marks)
where 2 ≤ n ≤ 50 (1983 - 3 Marks)
Ans. Sol. We must have one ace in (n – 1) attempts and one ace in the nth attempt. The probability of drawing one ace in first (n – 1) attempts is and other one ace in the
nth attempt is, 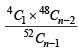 and other one ace in the nth attempt is,
and other one ace in the nth attempt is,
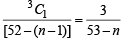
Hence the required probability,

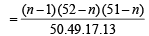
Q.6. A, B, C are events such that (1983 - 2 Marks) P (A) = 0.3, P(B) = 0.4, P (C) = 0.8
P (AB) = 0.08, P (AC) = 0.28; P (ABC)=0.09
If P( A ∪ B ∪ C )≥ 0.75 , then show that P (BC) lies in the interval 0.23 ≤ x ≤ 0.48
Ans. Sol. Given that P (A) = 0.3, P(B) = 0.4, P (C) = 0.8
P (AB) = 0.08, P (AC) = 0.28, P(ABC) = 0.09
P (A ∪ B ∪ C) ≥ 0.75
To find P (BC) = x (say) Now we know, P (A ∪ B ∪ C) = P (A) + P (B) + P (C)
– P (AB) – P (BC) – P (CA) + P (ABC)
⇒ P (A ∪ B ∪ C) = 0.3 + 0.4 + 0.8
– 0.08 – x – 0.28 + 0.09 = 1.23 – x
Also we have, P (A ∪ B ∪ C) ≥ 0.75 and P (A ∪ B ∪ C) ≤ 1
∴ 0.75 ≤ P (A ∪ B ∪ C) ≤ 1
⇒ 0.75 ≤ 1.23 – x ≤ 1 ⇒ 0.23 ≤ x ≤ 0.48
Q.7. In a certain city only two newspapers A and B are published, it is known that 25% of the city population reads A and 20% reads B while 8% reads both A and B. It is also known that 30% of those who read A but not B look into advertisements and 40% of those who read B but not A look into advertisements while 50% of those who read both A and B look into advertisements. What is the percentage of the population that reads an advertisement? (1984 - 4 Marks)
Ans. Sol. Let P (A) denotes the prob. of people reading newspaper A and P (B) that of people reading newspaper B
Then, 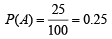

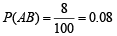
Prob. of people reading the newspaper A but not B = P (ABc) = P (A) – P (AB) = 0.25 – 0.08 = 0.17
Similarly, P (Ac B) = P (B) – P (AB) = 0.20 – 0.08 = 0.12
Let E be the event that a person reads an advertisement.
Therefore, ATQ, P (E / ABc) 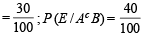
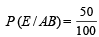
∴ By total prob. theorem (as ABc, AcB and AB are mutually exclusive)
P (E) = P (E / ABc) P (ABc) + P(E / AcB) P (AcB) + P (E / AB) . P (AB)
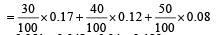
= 0.051 + 0.048 + 0.04 = 0.139.
Thus the population that reads an advertisement is 13.9%.
Q.8. In a multiple-choice question there are four alternative answers, of which one or more are correct. A candidate will get marks in the question only if he ticks the correct answers. The candidate decides to tick the answers at random, if he is allowed upto three chances to answer the questions, find the probability that he will get marks in the question s. (1985 - 5 Marks)
Ans. Sol. The total number of ways of ticking the answers in any one attempt = 24 – 1 = 15.
The student is taking chance at ticking the correct answer, It is reasonable to assume that in order to derive maximum benefit, the three solutions which he submit must be all different.
∴ n = total no. of ways = 15C3 m = the no. of ways in which the correct solution is excluded = 14 C3
Hence the required probability 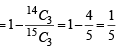
Q.9. A lot contain s 20 art icles. The probability th at th e lot contains exactly 2 defective articles is 0.4 and the probability that the lot contains exactly 3 defective articles is 0.6. Articles are drawn from the lot at random one by one without replacement and are tested till all defective articles are found.
What is the probability that the testing procedure ends at the twelth testing. (1986 - 5 Marks)
Ans. Sol. Let A1 be the event that the lot contains 2 defective articles and A2 the event that the lot contains 3 defective articles.
Also let A be the event that the testing procedure ends at the twelth testing. Then according to the question :
P (A1) = 0.4 and P (A2) = 0.6 Since 0 < P (A1) < 1, 0 < P (A2) < 1, and P (A1) + P (A2) = 1
∴ The events A1, A2 form a partition of the sample space.
Hence by the theorem of total probability for compound events, we have
P (A) = P (A1) P (A /A1) + P (A2) P (A/A2) … (1)
Here P (A /A1) is the probability of the event the testing procedure ends at the twelth testing when the lot contains 2 defective articles.
This is possible when out of 20 articles, first 11 draws must contain 10 non defective and 1defective article and 12th draw must give a defective article.
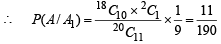
Similarly, 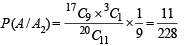
Now substituting the values of P (A /A1) and P (A /A2) in eq. (1), we get
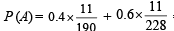
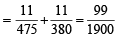
Q.10. A man takes a step for ward with probability 0.4 an d backwards with probability 0.6 Find the probability that at the end of eleven steps he is one step away from the starting point. (1987 - 3 Marks)
Ans. Sol. Since the man is one step away from starting point means that either (i) man has taken 6 steps forward and 5 steps backward. or (ii) man has taken 5 steps forward and 6 steps backward.
Taking movement 1 step forward as success and 1 step backward as failure.
∴ p = Probability of success = 0.4 and q = Probability of failure = 0.6
∴ Required probability = P (X = 6 or X = 5) = P (X = 6 ) + P (X = 5)
= 11C6 p6q5 + 11C5 p5 q6 = 11C5 (p6q5 + p5 q6) = 11C5 (p + q) ( p5 q5)
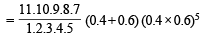
= 462 × 1 × (0.24)5 = 0.37
Hence the required prob. = 0.37
Q.11. A box contains 2 fifty paise coins, 5 twenty five paise coins and a certain fixed number N (≥ 2) of ten and five paise coins. Five coins are taken out of the box at random. Find the probability that the total value of these 5 coins is less than one rupee and fifty paise. (1988 - 3 Marks)
Ans. Sol. Here the total number of coins is N + 7.Therefore the total number of ways of choosing 5 coins out of N + 7 is N + 7C5.
Let E denotes the event that the sum of the values of the coins is less than one rupee and fifty paise.
Then E' denotes the event that the total value of the five coins is equal to or more than one rupee and fifty paise.
The number of cases favourable to E' is = 2C1 × 5C4 × NC0 + 2C2× 5C3 × NC0+ 2C2× 5C2 × NC1
= 2 × 5 + 10 + 10N = 10 (N + 2)
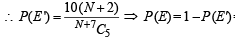
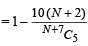
Q.12. Suppose the probability for A to win a game against B is 0.4.
If A has an option of playing either a “best of 3 games” or a “best of 5 games” match against B, which option should be choose so that the probability of his winning the match is higher? (No game ends in a draw). (1989 - 5 Marks)
Ans. Sol. The probability p1 (say ) of winning the best of three games is = the prob. of winning two games + the prob. of winning three games.
= 3C2 (0.6) (0.4)2 + 3C3 (0.4)3 [Using Binomial distribution]
Similarly the probability of winning the best five games is p2 (say) = the prob. of winning three games + the prob. of winning four games + the prob. of winning 5 games
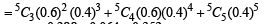
We have p1 = 0.288 + 0.064 = 0.352 and p2 = 0.2304 + 0.0768 + 0.01024 = 0.31744 As p1 > p2
∴ A must choose the first offer i.e. best of three games.
Q.13. A is a set containing n elements. A subset P of A is chosen at random. The set A is reconstructed by replacing the elements of P. A subset Q of A is again chosen at random.
Find the probability that P and Q have no common elements. (1990 - 5 Marks)
Ans. Sol. Let A = {a1, a2, a3,…,an}
For each ai, 1 ≤ i ≤ n, there aries 4 cases
(i) ai ∈P and ai ∈Q (ii) ai ∉P and ai ∈Q (iii) ai ∈P and ai ∉Q (iv) ai ∉P and ai ∉Q
∴ Total no. of ways of choosing P and Q is 4n. Here case (i) is not favourable as P ∩ Q = f
∴ For each element there are 3 favourable cases and hence total no. of favourable cases = 3n.
Hence prob. 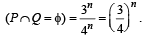
Q.14. In a test an examine either guesses or copies or knows the answer to a multiple choice question with four choices. The probability that he make a guess is 1/3 and the probability that he copies the answer is 1/6. The probability that his answer is correct given that he copied it, is 1/8. Find the probability that he knew the answer to the question given that he correctly answered it. (1991 - 4 Marks)
Ans. Sol. Let us define the events :
A1 ≡ the examinee guesses the answer,,
A2 ≡ the examinee copies the answer
A3 ≡ the examinee knows the answer,,
A ≡ the examinee answers correctly.
Then, 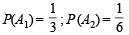
As any one happens out of A1, A2, A3, these are mutually exclusive and exhaustive events.
∴ P (A1) + P (A2) + P (A3) = 1
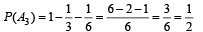
Also we have, P (A/A1) = 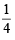
[∵ out of 4 choices only one is correct.] 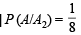
(given) P (A/A3) = 1
[If examinee knows the ans., it is correct. i.e. true event]
To find P (A3/A). By Baye’s thm, P (A3/A)
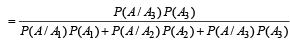
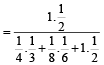
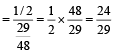
Q.15. A lot contains 50 defective and 50 non defective bulbs. Two bulbs are drawn at random, one at a time, with replacement.
The events A, B, C are defined as (1992 - 6 Marks)
A = (the first bulb is defective)
B = (the second bulb is non-defective)
C = (the two bulbs are both defective or both non defective) Determine whether
(i) A, B, C are pairwise independent (ii) A, B, C are independent
Ans. Sol. Let X = defective and Y = non defective. Then all possible outcomes are {XX, XY, YX, YY}
Also 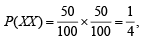
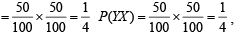
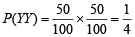
Here, A = XX ∪ XY ; B = XY ∪ YY ; C = XX ∪ YY
∴ P (A) = P(XX) + P (XY) 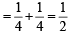
∴ P (B) = P (XY) + P (YX)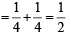
P (C) = P (XX) + P (YY) = 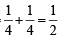
Now, 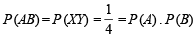
∴ A and B are independent events.
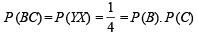
∴ B and C are independent events.
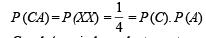
∴ C and A are independent events.
P (ABC) = 0 (impossible event) ≠ P (A) P (B) P (C)
∴ A, B, C are dependent events.
Thus we can conclude that A, B, C are pairwise independent but A, B, C are dependent events.
FAQs on Subjective Type Questions: Probability - 1 - JEE Advanced - Question Bank for JEE Main & Advanced (350+ Tests)
| 1. What is the definition of probability? |  |
| 2. How is probability calculated? |  |
| 3. What are the different types of probability? |  |
| 4. What is conditional probability? |  |
| 5. How can probability be used in real-life situations? |  |
















