Subjective Type Questions: Probability - 2 | JEE Advanced | Question Bank for JEE Main & Advanced (350+ Tests) PDF Download
Q.16. Numbers are selected at random, one at a time, from the twodigit numbers 00, 01, 02....., 99 with replacement. An event E occurs if only if the product of the two digits of a selected number is 18. If four numbers are selected, find probability that the event E occurs at least 3 times. (1993 - 5 Marks)
Ans. Sol. The given numbers are 00, 01, 02, …, 99.
These are total 100 numbers, out of which the numbers, the product of whose digits is 18, are 29, 36, 63 and 92.
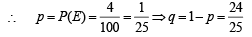
From Binomial distribution P (E occuring at least 3 times) = P (E occuring 3 times) + P (E occuring 4 times)
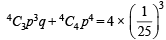
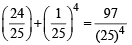
Q.17. An unbiased coin is tossed. If the result is a head, a pair of unbiased dice is rolled and the number obtained by adding the numbers on the two faces is noted. If the result is a tail, a card from a well shuffled pack of eleven cards numbered 2, 3, 4,.....12 is picked and the number on the card is noted.
What is the probability that the noted number is either 7 or 8? (1994 - 5 Marks)
Ans. Sol. E1 ≡ number noted is 7, E2 ≡ number notes is 8, H ≡ getting head on coin, T ≡ getting tail on coin.
Then by total probability theorem, P (E1) = P (H) P (E1/H) + P (T) P (E1/T)
and P (E2) = P (H) P (E2/H) + P (T) P (E2/T)
where 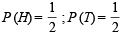
P (E1/H) = prob. of getting a sum of 7 on two dice. Here favourable cases are {(1, 6) , (6, 1), (2, 5), (5, 2), (3, 4), (4, 3)}
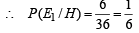
Also P (E1/ T) = prob. of getting '7' numbered card out of 11 cards = 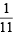
P (E2 / H) = Prob. of getting a sum of 8 on two dice. Here favourable cases are {(2, 6) (6, 2) (4, 4), (5, 3), (3, 5)}
∴ P (E2/H) = 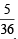
P (E2 / T) = prob. of getting '8' numbered card out of 11 car ds 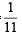
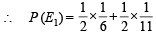
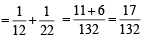
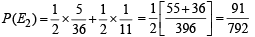
Now E1 and E2 are mutually exclusive events therefore
P (E1 or E2) = P (E1) + P (E2) =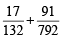
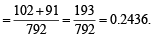
Q.18. In how many ways three girls and nine boys can be seated in two vans, each having numbered seats, 3 in the front and 4 at the back? How many seating arrangements are possible if 3 girls should sit together in a back row on adjacent seats?
Now, if all the seating arrangements are equally likely, what is the probability of 3 girls sitting together in a back row on adjacent seats? (1996 - 5 Marks)
Ans. Sol. We have 14 seats in two vans. And there are 9 boys and 3 girls.
The no. of ways of arranging 12 people on 14 seats without restriction is 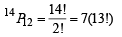
Now the no. of ways of choosing back seats is 2. And the no. of ways of arranging 3 girls on adjacent seats is 2 (3!).
And the no. of ways of arranging 9 boys on the remaining 11 seats is 11P9
Therefore, the required number of ways
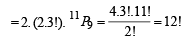
Hence, the probability of the required event 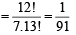
Q.19. If p and q are chosen randomly from the set {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, with replacement, determine the probability that the roots of the equation x2 + px + q = 0 are real. (1997 - 5 Marks)
Ans. Sol.
The required probability = 1– (probability of the event that the roots of x2 + px + q = 0 are non-real if and only if p2 – 4q < 0 i.e. if p2 < 4q.
We enumerate the possible values of p and q, for which this can happen in the following table.
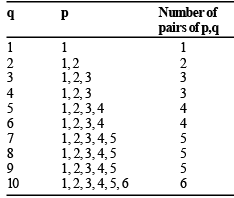
Thus, the number of possible pairs = 38. Also, the total number of possible pairs is 10 × 10 = 100.
∴ The required probability = 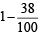 = 1 – 0.38 = 0.62.
= 1 – 0.38 = 0.62.
Q.20. Three players, A, B and C, toss a coin cyclically in that order (that is A, B, C, A, B, C,A,B, ....) till a head shows. Let p be the probability that the coin shows a head. Let a, b and g be, respectively, the probabilities that A, B and C gets the first head. Prove that b = (1 - p) a. Determine a, b and g (in terms of p). (1998 - 8 Marks)
Ans. Sol. Given that p is the prob. that coin shows a head then 1– p will be the prob. that coin shows a tail.
Now, α = P (A gets the 1st head in 1st try) + P (A gets the 1st head in 2nd try) + …
⇒ α = P (H) + P (T) P (T) P (T) P (H) + P (T) P (T) P (T) P (T) P (T) P (T) P (H)
= p + (1– p)3 p + (1– p)6 p+…… = p [1 + (1– p)3 (1 – p)6 +……] 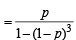
Similarly β = P (B gets the 1st head in 1st try) + P (B gets the 1st head in 2nd try) + ……
= P (T) P (H) + P (T) P (T) P (T) P (T) P(H) + ……
= (1– p) p + (1– p)4 p + …… 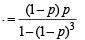 …(ii)
…(ii)
From (i) and (ii) we get b = (1– p) a
Also (i) and (ii) give expresion for α and β in terms of p.
Also α + β + γ = 1 (exhaustive events and mutually exclusive events)
⇒ γ = 1– α – β = 1– α – (1 – p)α
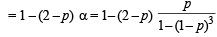
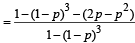
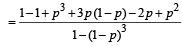

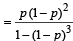
Q.21. Eight players P1, P2,........P8 play a knock-out tournament.
It is known that whenever the players Pi and Pj play, the player Pi will win if i < j. Assuming that the players are paired at random in each round, what is the probability that the player P4 reaches the final? (1999 - 10 Marks)
Ans. Sol. The number of ways in which P1, P2, …, P8 can be paired in four pairs
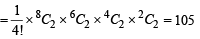
Now, at least two players certainly reach the second round in between P1, P2 and P3. And P4 can reach in final if exactly two players play against each other in between P1, P2, P3 and remaining player will play against one of the players from P5, P6, P7, P8 and P4 plays against one of the remaining three from P5, P6, P7, P8.
This can be possible in 3C2 × 4C1 × 3C1= 36 ways
∴ Prob. that P4 and exactly one of P5…P8 reach second
round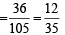
If P1, Pi, P4 and Pj where i = 2 or 3 and j = 5 or 6 or 7 reach the second round then they can be paired in 2 pairs in
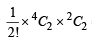 ways
ways
But P4 will reach the final if P1 plays against Pi and P4 plays against Pj.
Hence the prob. that P4 reach the final round from the second
=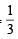
∴ prob. that P4 reach the final is 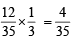
22. A coin has probability p of showing head when tossed. It is tossed n times. Let pn denote the probability that no two (or more) consecutive heads occur. Prove that p1=1, p2=1–p2 and pn=(1– p). pn–1 + p(1 – p) pn–2 for all n ≥ 3 . (2000 - 5 Marks)
Ans. Sol. Given that the probability of showing head by a coin when tossed = p
∴ Prob. of coin showing a tail = 1– p Now pn = prob. that no two or more consecutive heads occur when tossed n times.
∴ p1 = prob. of getting one or more or no head = prob. of H or T = 1
Also p2 = prob. of getting one H or no H = P (HT) + P (TH) + P (TT)
= p (1– p) + p (1–p) p + (1– p) (1– p) = 1– p2, For n ≥ 3 pn = prob. that no two or more consecutive heads occur when tossed n times. = P (last out come is T) P (no two or more consecutive heads in (n – 1) throw) + P (last out come is H) P ((n – 1)th throw results in a T) P (no two or more consecutive heads in (n – 2) n throws) = (1– p) Pn –1 + p (1– p) pn–2
Hence Proved.
23. An urn contains m white and n black balls. A ball is drawn at random and is put back into the urn along with k additional balls of the same colour as that of the ball drawn. A ball is again drawn at random. What is the probability that the ball drawn now is white? (2001 - 5 Marks)
Ans. Sol. Let W1 (B1) be the event that a white (a back) ball is drawn in the first draw and let W be the event that a white ball is drawn in the second draw.
Then P (W) = P (B1) . P (W/B1) + P (W1). P (W/W1)
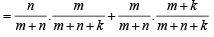
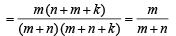
24. An unbiased die, with faces numbered 1, 2, 3, 4, 5, 6, is thrown n times and the list of n numbers showing up is noted. What is the probability that, among the numbers 1, 2, 3, 4, 5, 6, only three numbers appear in this list? (2001 - 5 Marks)
Ans. Sol. The total no. of outcomes = 6n
We can choose three numbers out of 6 in 6C3 ways. By using three numbers out of 6 we can get 3n sequences of length n.
But these include sequences of length n which use exactly two numbers and exactly one number.
The number of n-sequences which use exactly two numbers = 3C2 [2n – 1n – 1n] = 3 (2n –2) and the number of n sequences which are exactly one number = (3C1) (1n) = 3.
Thus , the number of sequences, which use exactly three numbers = 6C3 [3n – 3 (2n –2) –3] = 6C3[3n – 3(2n) + 3]
∴ Probability of the required event, 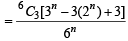
25. A box contains N coins, m of which are fair and the rest are biased. The probability of getting a head when a fair coin is tossed is 1/2, while it is 2/3 when a biased coin is tossed. A coin is drawn from the box at random and is tossed twice.
The first time it shows head and the second time it shows tail. What is the probability that the coin drawn is fair? (2002 - 5 Marks)
Ans. Sol. Let E1 be the event that the coin drawn is fair and E2 be the event that the coin drawn is biased.
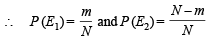
A is the event that on tossing the coin the head appears first and then appears tail.
∴ P (A) = P (E1∩ A) + P (E2 ∩ A)
= P (E1) P (A/E1) + P (E2) P (A/E2)
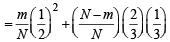 … (1)
… (1)
We have to find the probability that A has happened because of E1
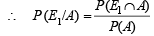
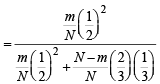 (by (1))
(by (1))
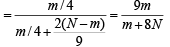
26. For a student to qualify, he must pass at least two out of three exams. The probability that he will pass the 1st exam is p. If he fails in one of the exams then the probability of his passing in the next exam is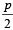 otherwise it remains the same. Find theprobability that he will qualify. (2003 - 2 Marks)
otherwise it remains the same. Find theprobability that he will qualify. (2003 - 2 Marks)
Ans. Sol. Let us consider E1 ≡ event of passing I exam.
E2 ≡ event of passing II exam.
E3 ≡ event of passing III exam.
Then a student can qualify in anyone of following ways
1. He passes first and second exam.
2. He passes first, fails in second but passes third exam.
3. He fails in first, passes second and third exam.
∴ Required probability = P (E1) P(E2/E1) + P (E1) P (E2/E1) P (E3/E2) + P (E1)
P (E2/E1) P (E3/E2)
[as an event is dependent on previous one]
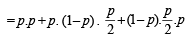
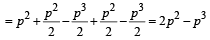
27. A is targeting to B, B and C are targeting to A. Probability of hitting the target by A, B and C are 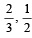 and
and 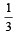 respectively..
respectively..
If A is hit then find the probability that B hits the target and C does not. (2003 - 2 Marks)
Ans. Sol. Let us consider the events
E1 ≡ A hits B Then P (E1) = 2/3
E2 ≡ B hits A P (E2) = 1/2
E3 ≡ C hits A P (E3) = 1/3 E ≡ A is hit
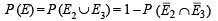

To find 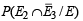
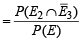
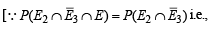 B hits A and A is hit = B hits A]
B hits A and A is hit = B hits A]
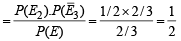
28. A an d B ar e two independent events. C is event in wh ich exactly one of A or B occurs. Prove that 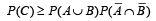 (2004 - 2 Marks)
(2004 - 2 Marks)
Ans. Sol. Given that A and B are two independent events. C is the event in which exactly of A or B occurs.
Let P (A) = x, P(B) = y then P(C) = 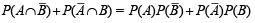
[∵ If A and B are independent so are ‘A and 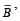 and
and 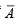 and B’.]
and B’.]
⇒ P (C) = x (1– y) + y (1– x) … (1)
Now consider, 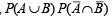
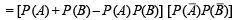
= (x + y – xy) (1– x) (1– y)
= (x + y) (1– x) (1– y) –xy (1–x) (1–y) ≤ (x + y) (1– x) (1– y) [∵ x,y ∈ (0,1)]
= x (1– x)(1– y) + y (1– x) (1– y)
= x (1– y) + y (1– x) – x2 (1– y) – y2 (1– x) ≤ x(1 - y) + y(1-x)3
= P (C) [Using eqn (1)]
Thus 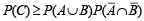 is proved.
is proved.
29. A box contains 12 red and 6 white balls. Balls are drawn from the box one at a time without replacement. If in 6 draws there are at least 4 white balls, find the probability that exactly one white is drawn in the next two draws. (binomial coefficients can be left as such) (2004 - 4 Marks)
Ans. Sol. Let us define the following events
A ≡ 4 white balls are drawn in first six draws
B ≡ 5 white balls are drawn in first six draws
C ≡ 6 white balls are drawn in first six draws
E ≡ exactly one white ball is drawn in next two draws (i.e. one white and one red)
Then P(E) = P (E/A) P (A) + P(E/B) P (B) + P (E/C) P (C) But P (E/C) = 0 [As there are only 6 white balls in the bag.]
P (E) = P (E/A) P(A) + P(E/B) P(B)
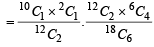
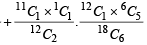
30. A person goes to office either by car, scooter, bus or train, the probability of which being 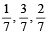 and
and 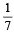 respectively..
respectively..
Probability that he reaches office late, if he takes car, scooter, bus or train is 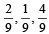 and
and 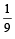 respectively. Given that hereached office in time, then what is the probability that he travelled by a car. (2005 - 2 Marks)
respectively. Given that hereached office in time, then what is the probability that he travelled by a car. (2005 - 2 Marks)
Ans. Sol. Let us define the following events
C ≡ person goes by car,
S ≡ person goes by scooter,
B ≡ person goes by bus,
T ≡ person goes by train,
L ≡ person reaches late
Then we are given in the question
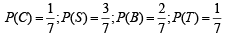
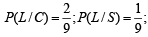
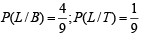
To find the prob. 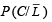 [∵ reaches in time ≡ not late] Using Baye’s theorem
[∵ reaches in time ≡ not late] Using Baye’s theorem
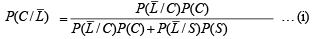
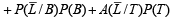
Now, 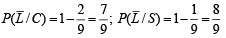
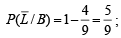
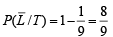
Substituting these values in eqn. (i) we get
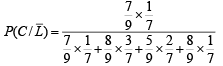


|
Explore Courses for JEE exam
|

|

















