Subjective Type Questions: Sequences and Series | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Q.1. The harmonic mean of two numbers is 4. Their arithmetic mean A and the geometric mean G satisfy the relation. 2A + G2 = 27
Find the two numbers. (1979)
Ans. 3 and 6 or 6 and 3
Sol. Let the two numbers be a and b, then
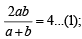
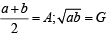
Also 2A + G2 = 27 ⇒ a + b + ab = 27 ....(2)
Putting ab = 27 – (a+b) in eqn. (1), we get
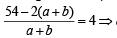 a + b = 9 then ab = 27 – 9 = 18
a + b = 9 then ab = 27 – 9 = 18
Solving the two we get a = 6, b = 3 or a = 3, b = 6, which are the required numbers.
Q.2. Th e in ter ior an gles of a polygon ar e in ar ith metic progression. The smallest angle is 120°, and the common difference is 5°, Find the number of sides of the polygon. (1980)
Ans. 9
Sol. Let there be n sides in the polygon.
Then by geometry, sum of all n interior angles of polygon = (n – 2) × 180° Also the angles are in A.P. with the smallest angle = 120° , common difference = 5° ∴ Sum of all interior angles of polygon

Thus we should have
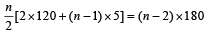
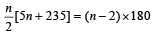
⇒ 5n2 + 235n= 360n- 720
⇒ 5n2 - 125n + 720= 0
⇒ n2 - 25n + 144= 0
⇒ (n -16) (n - 9)= 0
⇒ n = 16, 9
Also if n = 16 then 16th angle = 120 + 15 × 5 = 195° > 180°
∴ not possible. Hence n = 9.
Q.3. Does there exist a geometric progression containing 27, 8 and 12 as three of its terms ? If it exits, how many such progressions are possible ? (1982 - 3 Marks)
Ans. yes, infinite
Sol. If possible let for a G.P.
Tp= 27 = ARp–1 ....(1)
Tq= 8 = ARq–1 ....(2)
Tr= 12 = ARr–1 ....(3)
From (1) and (2)
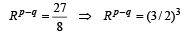 ....(4)
....(4)
From (2) and (3):
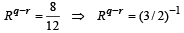 ....(5)
....(5)
From (4) and (5):
R = 3/2; p – q = 3 ; q – r = – 1 p – 2q + r = 4; p, q, r ∈ N ....(6)
As there can be infinite natural numbers for p, q and r to satisfy equation (6)
∴ There can be infinite G.P’s.
Q.4. Find three numbers a, b, c, between 2 and 18 such that (i) their sum is 25 (ii) the numbers 2, a, b sare consecutive terms of an A.P. and (iii) the numbers b, c, 18 are consecutive terms of a G.P. (1983 - 2 Marks)
Ans. a = 5, b = 8, c = 12
Sol. 2 < a, b, c < 18 a + b + c = 25 ....(1)
2, a, b are in AP ⇒ 2a = b + 2 ⇒ 2a – b = 2 ....(2)
b, c, 18 are in GP ⇒ c2 = 18b ....(3)
From (2) 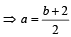
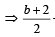 +
+ 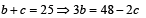
(3) ⇒ c2 = 6 (48 - 2c) ⇒ c2 + 12c - 288= 0
⇒ c = 12, – 24 (rejected) ⇒ a = 5, b = 8, c = 12
Q. 5. If a > 0, b > 0 and c > 0, prove that
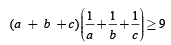 (1984 - 2 Marks)
(1984 - 2 Marks)
Ans. Sol. Given that a, b, c > 0
We know for +ve numbers A.M. ≥ G.M.
∴ For +ve numbers a, b, c we get
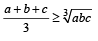 ....(1)
....(1)
Also for +ve numbers 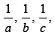 we get
we get
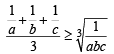 ....(2)
....(2)
Multiplying in eqs (1) and (2) we get
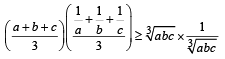
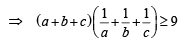 Proved.
Proved.
Q.6. If n is a natural number such that
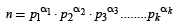 an d p1, p2, ....., pk are distinct primes, then show that ln n ≥ k ln2 (1984 - 2 Marks)
an d p1, p2, ....., pk are distinct primes, then show that ln n ≥ k ln2 (1984 - 2 Marks)
Ans. Sol. Given that 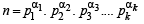 ....(1)
....(1)
Where n∈N and p1, p2, p3, ......pk are distinct prime numbers.
Taking log on both sides of eq. (1),
we get log n = α1 log p1+ α2 log p2 + ....+ ak log pk ....(2)
Since every prime number is such that
pi ≥ 2
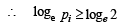 ....(3)
....(3)
∀ i= 1 (1) k Using (2) and (3)
we get log n ≥ α1 log 2 + α2 log 2 + α3 log 2 + ....+ αk log 2
⇒ log n ≥ (α1+α2+ ....+ αk) log 2
⇒ log n ≥ k log 2 Proved.
Q.7. Find the sum of the series :
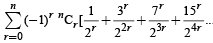 ... up to terms]
... up to terms]
Ans. Sol. The given series is
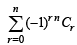
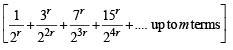
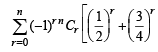
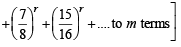
Now, 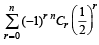
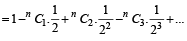

Similarly, 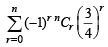

Hence the given series is,
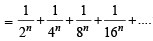 .... to terms
.... to terms
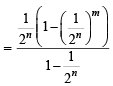 [ Summing the G.P.]
[ Summing the G.P.]
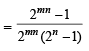
Q.8. Solve for x the following equation : (1987 - 3 Marks)
log(2 x +3) (6 x2 + 23x + 21) = 4 - log (3x+7) (4 x2 + 12x+ 9)
Ans. -1/4
Sol. The given equation is log (2x + 3) (6x2 + 23 + 21)
= 4 – log3x+7 (4x2 + 12x + 9)
⇒ log(2x+3) (6x2 + 23x + 21) + log(3x+7) (4x2 + 12x + 9) = 4
⇒ log(2x+3) (2x + 3) (3x + 7) + log(3x+7) (2x + 3)2 x =4
⇒ 1+log(2x+3) (3x + 7) + 2log(3x+7) (2x + 3) =4
⇒ log(2x+3)(3x + 7) +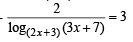
Let log(2x+3)(3x + 7) = y ....(1)
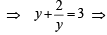 y2 -3y+2=0
y2 -3y+2=0
⇒ (y – 1) (y – 2) = 0 ⇒ y = 1, 2
Substituting the values of y in (1), we get
⇒ log(2x+3)(3x + 7) = 1 and log(2x+3)(3x + 7) = 2
⇒ 3x + 7 = 2x + 3 an d3x + 7 = (2x + 3)2
⇒ x = – 4 an d4x2 + 9x + 2 = 0
⇒ x = – 4 an d(x + 2) (4x + 1) = 0
⇒ x = – 4 and x = – 2, x = – 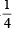
As log a x is defined for x > 0 and a > 0 (a ≠ 1), the possible value of x should satisfy all of the following inequalities :
⇒ 2x + 3 > 0 and 3x + 7 > 0
Also 2x + 3 ≠ 1 and 3x + 7 ≠ 1
Out of x = – 4, x = – 2 an d x = –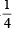 only x = –
only x = – 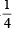
satisfies the above inequalities.
So only solution is x = –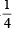
Q. 9. If log 3 2 , log3 (2 x , 5) , and  are in arithmetic progression, determine the value of x. (1990 - 4 Marks)
are in arithmetic progression, determine the value of x. (1990 - 4 Marks)
Ans. 3
Sol. Given that log3 2, log3 (2x – 5), log3 (2x –7/2) are in A.P.
⇒ 2 log3 (2x – 5) = log3 2 + log3 (2x – 7/2)
⇒ (2 x - 5) 2 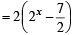
⇒ (2x)2 – 10.2x + 25 – 2.2x + 7 = 0 ⇒ (2x)2 – 12.2x + 32 = 0
Let 2x = y, then we get, y2 – 12y + 32 = 0
⇒ (y – 4) (y – 8) = 0
⇒ y = 4 or 8
⇒ 2x = 22 or 23 ⇒ x = 2 or 3
But for log3 (2x – 5) and log3 (2x – 7/2) to be defined
2x – 5 > 0 and 2x – 7/2 > 0 ⇒ 2x > 5 and 2x > 7/2
⇒ 2x > 5 ⇒ x ≠ 2 and therefore x = 3.
Q.10. Let p be the first of the n arithmetic means between two numbers and q the first of n harmonic means between the same numbers. Show that q does not lie between p and
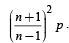 (1991 - 4 Marks)
(1991 - 4 Marks)
Ans. Sol. Let a and b be two numbers and A1, A2, A3, .... An be n A.M’s between a and b.
Then a, A1, A2, ..... An, b are in A.P.
There are (n + 2) terms in the series, so that
a + (n + 1) d = b 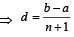
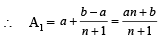
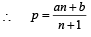 ....(1)
....(1)
The first H.M. between a and b, when nHM’s are inserted between a and b can be obtained by replacing a by 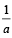 and b by
and b by 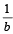 in eq. (1) and then taking its reciptocal.
in eq. (1) and then taking its reciptocal.
Therefore, 
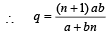 ...(2)
...(2)
We have to prove that q cannot lie between p
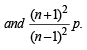
Now, n + 1>n –1 
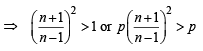
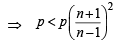 ....(3)
....(3)
Now to prove the given, we have to show that q is less than p.
For this, let, 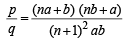
⇒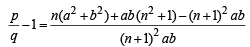
⇒ 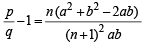
⇒ 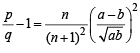
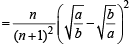
⇒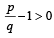
⇒ (provided a and b and hence p and q are +ve) p > q ....(4)
From 3 and (4), we get, 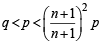
∴ q can not lie between p and 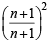 p, if a and b are +ve numbers.
p, if a and b are +ve numbers.
Q.11. If S1, S2 ,S3, ............... , Sn are the sums of infinite geometric series whose first terms are 1, 2, 3, ..............., n and whose common ratios are
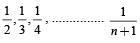 respectively,,then find the values of
respectively,,then find the values of  (1991 - 4 Marks)
(1991 - 4 Marks)
Ans. Sol. We have,
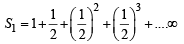
....................................................
....................................................
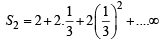
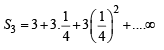
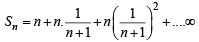
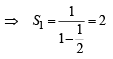
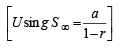
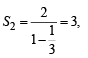
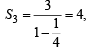
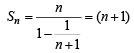
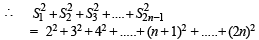
NOTE THIS STEP :
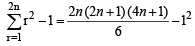
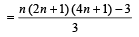
Q.12. The real numbers x1, x2, x 3 s atis fying the equation x3 , x2 + βx + γ < 0 are in AP. Find the intervals in which β and γ lie. (1996 - 3 Marks)
Ans. Sol. Since x1, x2, x3 are in A.P.
Therefore, let x1 = a – d, x2 = a and x3 = a + d and x1, x2, x3 are the roots of x3 – x2 + βx + γ =0
We have ∑α = a – d + a + a + d = 1 ....(1)
∑αβ = (a – d) a + a ( a + d) + (a – d) (a + d) = b ....(2)
αβγ = (a – d) a (a + d) = – γ ....(3)
From (1), we get, 3a = 1 ⇒ a = 1/3
From (2), we get, 3a2 – d2 = β
⇒ 3(1/3)2 – d2 = β ⇒ 1/3 – β = d2
We know that d2 > 0 ∀ d ∈ R
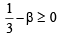 ∵ d 2 ≥ 0
∵ d 2 ≥ 0
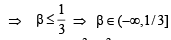
From (3), a (a2 – d2) = – γ
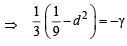
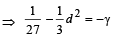
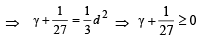
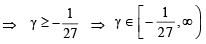
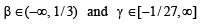
Q.13. Let a, b, c, d be real numbers in G.P. If u, v, w, satisfy the system of equations (1999 - 10 Marks)
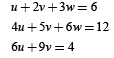
then show that the roots of the equation
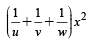
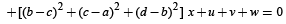
and 20x2 + 10 (a - d)2 x - 9 = 0 are reciprocals of each other.
Ans.
Sol. Solving the system of equations, u + 2v + 3w = 6,
4u + 5v + 6w = 12 and 6u + 9v = 4
we get u = – 1/3, v = 2/3, w = 5/3
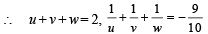
Let r be the common ratio of the G.P., a, b, c, d. Then b = ar, c = ar2, d = ar3 .
Then the first equation
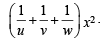 + [(b – c)2 + (c – a)2 + (d – b)2]x + (u + v + w) = 0 becomes
+ [(b – c)2 + (c – a)2 + (d – b)2]x + (u + v + w) = 0 becomes
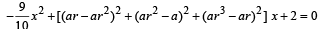
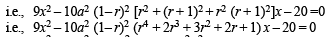
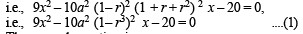
The second equation is, 20 x2 + 10 (a – ar3)2 x – 9 = 0
i.e., 20 x2 + 10 a2 (1 – r3)2 x – 9 = 0 ....(2)
Since (2) can be obtained by the substitution x → 1/x , equations (1) and (2) have reciprocal roots.
Q.14. The fourth power of the common difference of an arithmatic progression with integer entries is added to the product of any four consecutive terms of it. Prove that the resulting sum is the square of an integer. (2000 - 4 Marks)
Ans.
Sol. Let a – 3d, a – d, a + d and a + 3d be any four consecutive terms of an A.P. with common difference 2d.
∵ Terms of A.P. are integers, 2d is also an integer.
Hence P = (2d)4 + (a – 3d) (a – d) (a + d) (a + 3d)
=16 d 4 + (a 2 – 9 d 2) (a 2 – d 2) = (a 2 – 5 d 2)2
Now, a 2 – 5 d 2 = a 2 – 9 d 2 + 4 d 2 = (a – 3 d) (a + 3 d) + (2 d)2 = some integer
Thus, P = square of an integer.
Q.15. Let a1, a2, …, an be positive real numbers in geometric progression. For each n, let An, Gn, Hn be respectively, the arithmetic mean, geometric mean, and harmonic mean of a1, a2, …, an. Find an expression for the geometric mean of G1, G2, …, Gn in terms of A1, A2 , …, An, H1, H2, …, Hn. (2001 - 5 Marks)
Ans.
Sol. Given that a1, a2, ....an are +ve real no’s in G.P.
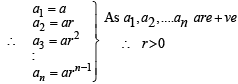
An is A.M. of a1, a2, ....., an
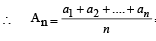
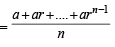
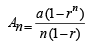 .... (1) (For r ≠ 1)
.... (1) (For r ≠ 1)
Gn is G.M. of a1, a2, ...., an
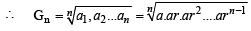

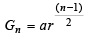 .... (2) (r ≠ 1)
.... (2) (r ≠ 1)
Hn is H.M. of a1, a2, ....., an
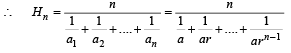
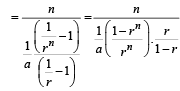
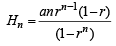 (r ≠ 1) ...(3)
(r ≠ 1) ...(3)
We also observe that
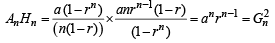
∴ An Hn =Gn2....(4)
∴ Now, G.M. of G1, G2, .... Gn is
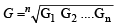
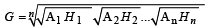 [Using equation (4)
[Using equation (4)
G = (A1A2....AnH1H2....Hn)1/2n ...(5)
If r = 1 then An = Gn = Hn = a
Also An Hn = Gn2
∴ For r = 1 also, equation (5) holds.
Hence we get, G = (A1A2....AnH1H2....Hn)1/2n
Q.16. Let a, b be positive real numbers. If a, A1, A2, b are in arithmetic progression, a, G1, G2, b are in geometric progression and a, H1, H2, b are in harmonic progression,
show that 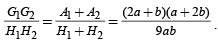 (2002 - 5 Marks)
(2002 - 5 Marks)
Ans.
Sol. Clearly A1 + A2 = a + b
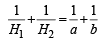
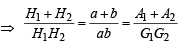
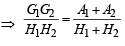
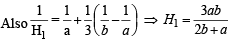

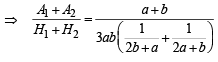
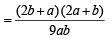
Q.17. If a, b, c are in A.P., a2, b2, c2 are in H.P., then prove that either a = b = c or a, b, 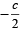 form a G.P.. (2003 - 4 Marks)
form a G.P.. (2003 - 4 Marks)
Ans.
Sol. Given that a, b, c are in A.P.
⇒ 2b = a + c ....(1)
and a2, b2, c2 are in H.P.
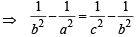
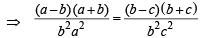
⇒ ac2 + bc2 = a2b + a2c [∵ a – b = b – c]
⇒ ac (c – a) + b (c – a) (c + a) = 0
⇒ (c – a) (ab + bc + ca) = 0
⇒ either c – a = 0 or ab + bc + ca = 0
⇒ either c = a or (a + c) b + ca = 0 and then from (i)
2b2 + ca = 0
Either a = b = c 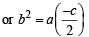
i.e. a, b, – c/2 are in G.P. Hence Proved.
Q.18. If an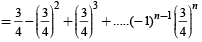 and
and
bn = 1 – an, then find the least natural number n0 such that
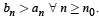 (2006 - 6M)
(2006 - 6M)
Ans.
Sol.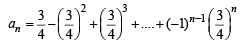
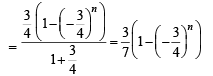
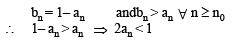
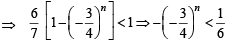
⇒ (– 3)n +1 < 22n–1 For n to be even, inequality always holds. For n to be odd, it holds for n ≥ 7.
∴ The least natural no., for which it holds is 6
(∵ it holds for every even natural no.)
|
347 docs|185 tests
|
|
347 docs|185 tests
|

|
Explore Courses for JEE exam
|

|

















