Subjective Type Questions: Vector Algebra and Three Dimensional Geometry - 2 | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
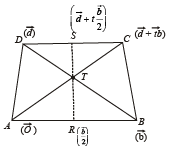
Q. 16. Prove, by vector methods or otherwise, that the point of intersection of the diagonals of a trapezium lies on the line passing through the mid-points of the parallel sides. (You may assume that the trapezium is not a parallelogram.) (1998 - 8 Marks)
Solution. The P.Vs. of the points A, B, C, D are
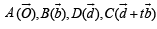
Equations of AC and BD are
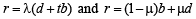
For point of intersection say T compare the coefficients
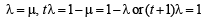
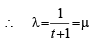
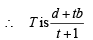 ...(1)
...(1)
Let R and S be mid-points of parallel sides AB and DC then

Equation of RS by r = a + s(b-a) is
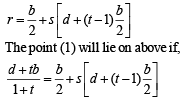
Comparing the coefficients, we get
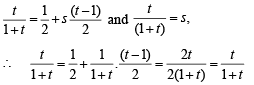
which is true . Hence proved.
Q. 17. For any two vectors u and v, prove that (1998 - 8 Marks)

Solution. We have, 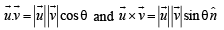 Where θ is the angle between
Where θ is the angle between  is a unit vector perpendicular to both
is a unit vector perpendicular to both 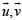 and is such that
and is such that 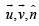 form a right handed system.
form a right handed system.
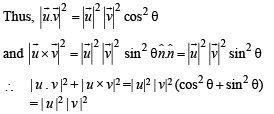
(b) 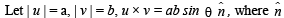 is perpendicular to both u and v , | a |2 = a2
is perpendicular to both u and v , | a |2 = a2
L.H.S. = (1 + a2) (1 + b2)
R.H.S. = (1 - ab cos qθ)2 + (u + v)2 (u × v)2 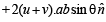
= 1 + a2b2 cos2 θ - 2ab cos θ +a2 +b2 + 2abcos θ + a2b2 sin2 θ.1+ 0
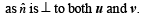
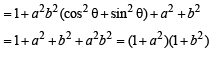
Q. 18. Let u an d v be unit vector s. If w is a vector such th at w +(w × u) = v, then prove that |(u × v) · w| < 1/2 and that the equality holds if and only if u is perpendicular to v. (1999 - 10 Marks)
Solution. 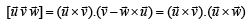
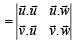
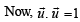
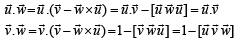
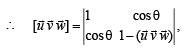
(θ is angle between 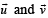 )
)
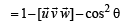
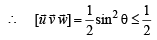
Equality holds when 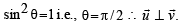
Q. 19. Show, by vector methods, that the angular bisectors of a triangle are concurrent and find an expression for the position vector of the point of concurrency in terms of the position vectors of the vertices. (2001 - 5 Marks)
Solution. Let  be the position vectors by A, B, and C respectively,
be the position vectors by A, B, and C respectively,
Let AB, BE and CF be the bisectors of ∠A, ∠B , and ∠C respectively.
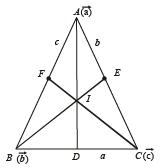
a, b, c are the lengths of sides BC, CA and AB respectively.
Now we know by angle bisector thm that AD divides, BC in the ratio
BD : DC = AB : AC = c : b.
∴ The position vector of D is 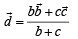
Let I be the point of intersection of BE and AD. Then in ΔABD, BI is bisector of ∠B.
∴ DI : IA = BD : BA

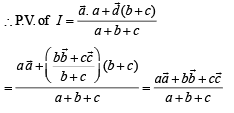
As p.v. of I is symm. in 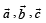 and a,b,c.
and a,b,c.
∴ It must lie on CF as well.
[We can also see that p.v. of intersection of 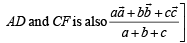
Above prove that all the ∠ bisectors pass through I, i.e., these are concurrent.
Q. 20. Find 3-dimensional vectors 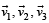 satisfying
satisfying 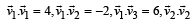
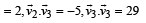 (2001 - 5 Marks)
(2001 - 5 Marks)
Ans. 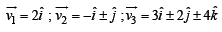 are some possible values.
are some possible values.
Solution. Given data is insufficient to uniquely determine the three vectors as there are only 6 equations involving 9 variables.
∴ We can obtain infinitely many set of three vectors,
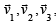 satisfying these conditions.
satisfying these conditions.
From the given data, we get
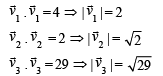
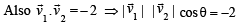
[where θ is the angle between 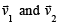 ]
]
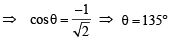
Now since any two vectors are always coplanar, let us suppose that 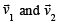 are in x-y plane.
are in x-y plane.
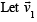 is along the positive direction of x-axis
is along the positive direction of x-axis
then 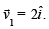
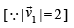
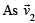 makes an angle 135° with
makes an angle 135° with 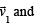 lines in x-y plane,
lines in x-y plane,
Also keeping in mind
are some possible answers.
Q. 21. 
 where f1, f2, g1, g2 are continuous functions. If
where f1, f2, g1, g2 are continuous functions. If  and
and  are nonzero vectors for all t and
are nonzero vectors for all t and 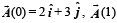
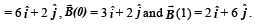 Then show that
Then show that 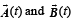 are parallel for some t. (2001 - 5 Marks)
are parallel for some t. (2001 - 5 Marks)
Solution.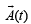 is parallel to
is parallel to 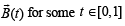 if and only if
if and only if
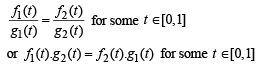
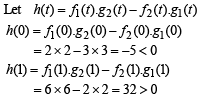
Since h is a continuous function, and h(0).h(1) < 0
⇒ There is some t ∈ [0,1] for which h(t) = 0 i.e., 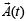 and
and 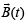 are parallel vectors for this t.
are parallel vectors for this t.
Q. 22. Let V be the volume of the parallelopiped formed by the vectors 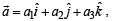
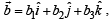
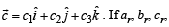 where r = 1, 2, 3, are n on negative real numbers and
where r = 1, 2, 3, are n on negative real numbers and 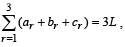 show that
show that 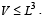 (2002 - 5 Marks)
(2002 - 5 Marks)
Solution.

⇒ V = (a1b2c3 + a2b3c1+ a3b1c2) - (a1b3c2 + a2b1c3+ a3b2c1) ....(1)
Now we know that AM > GM
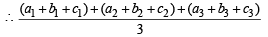
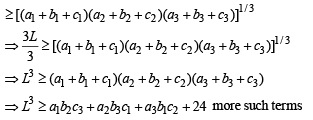
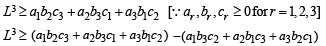
[same reason]
L3 > V from (1) Hence Proved.
Q. 23. (i) Find the equation of the plane passing through the points (2, 1, 0), (5, 0, 1) and (4, 1, 1). (2003 - 4 Marks)
(ii) If P is the point (2, 1, 6) then find the point Q such that PQ is perpendicular to the plane in (i) and the mid point of PQ lies on it.
Ans. (i) x + y - 2z = 3
(ii) Q(6, 5, - 2)
Solution. (i) Plane passing thr ough (2, 1, 0) , (5, 0, 1) and (4, 1, 1) is
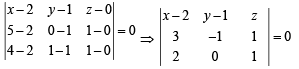
⇒ ( x - 2)(-1 - 0) - (y - 1)(3- 2) + z(0 - (-2)) = 0
⇒ -x + 2 - y +1+ 2z = 0 ⇒ x + y - 2z = 3
(ii) As per question we have to find a pt. Q such that PQ is ⊥ to the plane x + y - 2z = 3 ...(1)
And mid pt. of PQ lies on the plane, (Clearly we have to find image of pt. P with respect to plane).
Let Q be (α, β,γ)
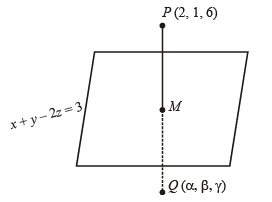
Eqn of PM passing through P(2, 1, 6) and ⊥ to plane x + y - 2z = 3 , is given by
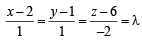
For some value of 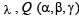 lies on PM
lies on PM

But M lies on plane (1)
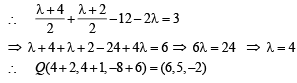
Q. 24. If 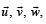 are three non-coplanar unit vectors and
are three non-coplanar unit vectors and 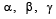 are the angles between
are the angles between 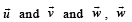 and
and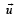 respectively and
respectively and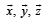 are unit vectors along the bisectors of the angles
are unit vectors along the bisectors of the angles 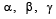 respectively. Prove that
respectively. Prove that 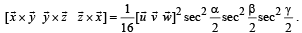 (2003 - 4 Marks)
(2003 - 4 Marks)
Solution. Given that  are three non coplanar unit vectors. Angle
are three non coplanar unit vectors. Angle  and between
and between 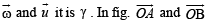 represent
represent 
Let P be a pt. on angle bisector of ∠AOB such that OAPB is a parallelogram
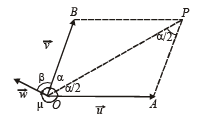
Also ∠POA =∠BOP = α /2
∴ ∠APO = ∠BOP = α /2 (alt. int. ∠ 's)
∴ In ΔOAP, OA= AP a unit vector in the direction of 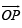
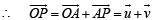
∴A unit vector in the direction of
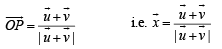
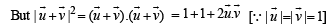
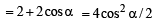
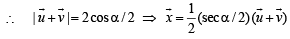
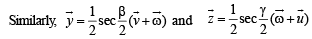
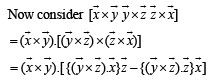
[Using defn of vector triple product.]
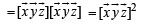 ...(1)
...(1)
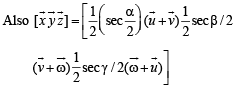
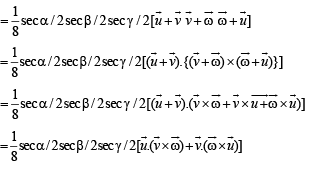
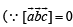 when ever any two vectors are same)
when ever any two vectors are same)

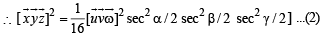
From (1) and (2),
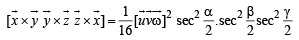
Q. 25. If 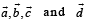 are distinct vectors such that
are distinct vectors such that 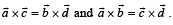
Prove that 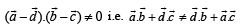 (2004 - 2 Marks)
(2004 - 2 Marks)
Solution. Given that 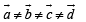
Such that 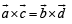 ...(1)
...(1)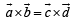 ...(2)
...(2)
To prove 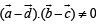
Subtracting eqn (2) from (1) we get
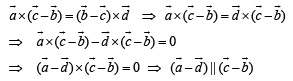
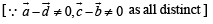
⇒ Angle between 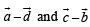 is either 0 or 180° .
is either 0 or 180° .
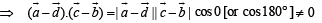
as a, b, c, d all are different. Hence Proved.
Q. 26. Find the equation of plane passing through (1, 1, 1) & parallel to the lines L1, L2 having direction ratios (1,0, –1), (1, –1,0). Find the volume of tetrahedron formed by origin and the points where these planes intersect the coordinate axes. (2004 - 2 Marks)
Ans. 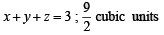
Solution. ∴ The plane is parallel to the lines L1 and L2 with direction ratios as (1, 0, –1) and (1, –1, 0)
∴ A vector perpendicular to L1 and L2 will be parallel to the normal 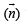 to the plane.
to the plane.
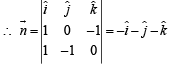
∴ Eqn. of plane through (1, 1, 1) and having normal vector 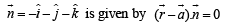
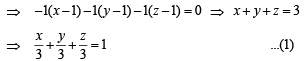
Now the pts where this plane meets the axes are A(3, 0, 0), B(0, 3, 0),C (0, 0, 3)
∴ Vol.of tetrahedron OABC
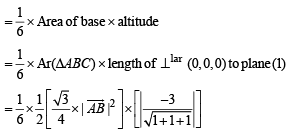
(Note that ΔABC is an equilateral Δ here.)
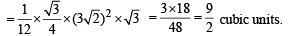
Q. 27. A parallelopiped ‘S’ h as base points A, B, C an d D and upper face points A', B', C' and D'. This parallelopiped is compressed by upper face A'B'C'D' to form a new parallelopiped ‘T’ having upper face points A'', B'', C'' and D''. Volume of parallelopiped T is 90 percent of the volume of parallelopiped S. Prove that the locus of ‘A''’, is a plane. (2004 - 2 Marks)
Solution. ATQ ‘S’ is the parallelopiped with base points A, B, C and D and upper face points A', B',C' and D ' . Let its vol. be Vs .
By compr essi n g it by upper face A', B', C ',D', a n ew parallelopiped ‘T’ is formed whose upper face pts are now A'',B'',C'' and D ''. Let its vol. be VT .
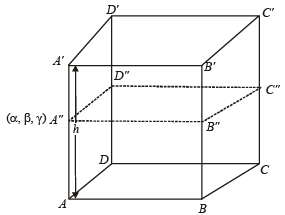
Let h be the height of original parallelopiped S.
Then VS = (ar ABCD)x h ...(1)
Let equation of plane ABCD be ax + by +cz +d= and A''(α,β,γ)
Then height of new parallelopipe T is the length of perpendicular from A'' to ABCD
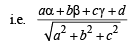
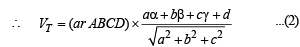
But given that,
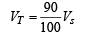 ...(3)
...(3)
From (1), (2) and (3) we get,
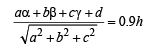
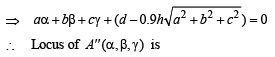
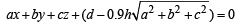
which is a plane parallel to ABCD . Hence proved.
Q. 28. P1 and P2 are planes passing through origin. L1 and L2 are two line on P1 and P2 respectively such that their intersection is origin. Show that there exists points A, B, C, whose permutation A', B', C' can be chosen such that (i) A is on L1, B on P1 but not on L1 and C not on P1 (ii) A' is on L2, B' on P2 but not on L2 and C' not on P2 (2004 - 4 Marks)
Solution. Following fig. shows the possible situation for planes P1 and P2 and the lines L1 and L2
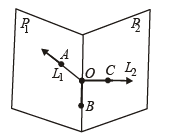
Now if we choose pts A, B, C as follows.
A on L1 , B on the line of intersection of P1 and P2 but other than origin and C on L2 again other than origin then we can consider
A corresponds to one of A',B',C' and
B corresponds to one of the remaining of A', B',C' and
C corresponds to third of A',B',C' e.g.
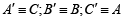
Hence one permutation of [ABC] is [CBA]. Hence Proved.
Q. 29. Find the equation of the plane containing the line 2x – y + z – 3 = 0, 3x + y + z = 5 and at a distance of 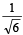 from the point(2, 1, –1) (2005 - 2 Marks)
from the point(2, 1, –1) (2005 - 2 Marks)
Ans. 62 x + 29 y + 19z - 105 = 0
Solution. The given line is 2x - y + z - 3 = 0 = 3x + y + z - 5
Which is intersection line of two planes
2 x - y + z - 3 = 0 ...(i)
and 3x + y + z - 5 = 0 ...(ii)
Any plane containing this line will be the plane passing through the intersection of two planes (i) and (ii).
Thus the plane containing given line can be written as

As its distance from the pt. 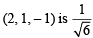
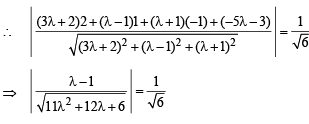
Squaring both sides, we get
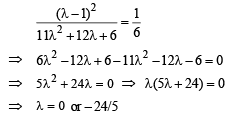
∴ The required equations of planes are 2x- y+z-3 = 0
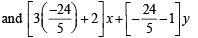
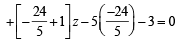
or 62x + 29 y + 19z - 105 = 0
Q. 30. If the incident ray on a surface is along the unit vector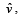 the reflected ray is along the unit vector
the reflected ray is along the unit vector 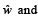 the normal is along unit vector
the normal is along unit vector 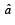 outwards. Express
outwards. Express 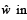 in terms of
in terms of 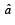 and
and 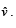 (2005 - 4 Marks)
(2005 - 4 Marks)
Ans. 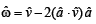
Solution. Given that incident ray is along  reflected ray is along
reflected ray is along 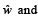 normal is along
normal is along 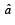 , outwards. The given figure can be redrawn as shown.
, outwards. The given figure can be redrawn as shown.
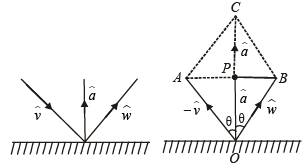
We know that incident ray, reflected ray and normal lie in a plane, and angle of incidence = angle of reflection.
Therefore 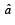 , will be along the angle bisector of
, will be along the angle bisector of 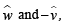
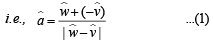
[∵ Angle bisector will along a vector dividing in same ratio as the ratio of the sides forming that angle.]
But 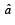 is a unit vector.
is a unit vector.
Where 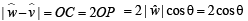
Substituting this value in equation (1) we get
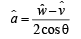
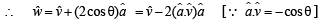
|
347 docs|185 tests
|
|
347 docs|185 tests
|

|
Explore Courses for JEE exam
|

|

















