Substitution Rule for Definite Integrals | Calculus - Mathematics PDF Download
We now need to go back and revisit the substitution rule as it applies to definite integrals. At some level there really isn’t a lot to do in this section. Recall that the first step in doing a definite integral is to compute the indefinite integral and that hasn’t changed. We will still compute the indefinite integral first. This means that we already know how to do these. We use the substitution rule to find the indefinite integral and then do the evaluation.
There are however, two ways to deal with the evaluation step. One of the ways of doing the evaluation is the probably the most obvious at this point, but also has a point in the process where we can get in trouble if we aren’t paying attention.
Let’s work an example illustrating both ways of doing the evaluation step.
Example 1: Evaluate the following definite integral.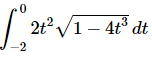
Solution : Let’s start off looking at the first way of dealing with the evaluation step. We’ll need to be careful with this method as there is a point in the process where if we aren’t paying attention we’ll get the wrong answer.
We’ll first need to compute the indefinite integral using the substitution rule. Note however, that we will constantly remind ourselves that this is a definite integral by putting the limits on the integral at each step. Without the limits it’s easy to forget that we had a definite integral when we’ve gotten the indefinite integral computed.
In this case the substitution is,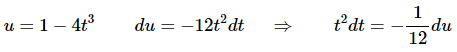
Plugging this into the integral gives,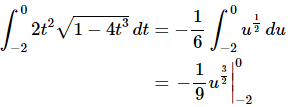
Notice that we didn’t do the evaluation yet. This is where the potential problem arises with this solution method. The limits given here are from the original integral and hence are values of t. We have u’s in our solution. We can’t plug values of t in for u.
Therefore, we will have to go back to t’s before we do the substitution. This is the standard step in the substitution process, but it is often forgotten when doing definite integrals. Note as well that in this case, if we don’t go back to t’s we will have a small problem in that one of the evaluations will end up giving us a complex number.
So, finishing this problem gives,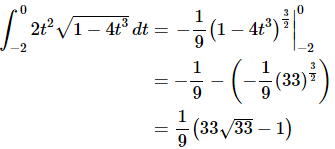
So, that was the first solution method. Let’s take a look at the second method.
Solution 2:
Note that this solution method isn’t really all that different from the first method. In this method we are going to remember that when doing a substitution we want to eliminate all the t’s in the integral and write everything in terms of u.When we say all here we really mean all. In other words, remember that the limits on the integral are also values of t and we’re going to convert the limits into u values. Converting the limits is pretty simple since our substitution will tell us how to relate t and u so all we need to do is plug in the original t limits into the substitution and we’ll get the new u limits.Here is the substitution (it’s the same as the first method) as well as the limit conversions.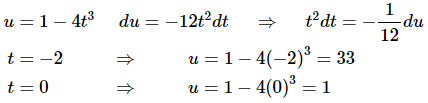
The integral is now,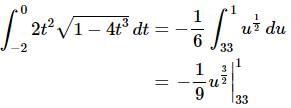
As with the first method let’s pause here a moment to remind us what we’re doing. In this case, we’ve converted the limits to u’s and we’ve also got our integral in terms of u’s and so here we can just plug the limits directly into our integral. Note that in this case we won’t plug our substitution back in. Doing this here would cause problems as we would have t’s in the integral and our limits would be u’s. Here’s the rest of this problem.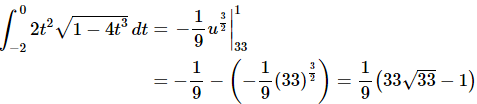
We got exactly the same answer and this time didn’t have to worry about going back to
t’s in our answer.
So, we’ve seen two solution techniques for computing definite integrals that require the substitution rule. Both are valid solution methods and each have their uses. We will be using the second almost exclusively however since it makes the evaluation step a little easier.
Let’s work some more examples.
Example 2: Evaluate each of the following.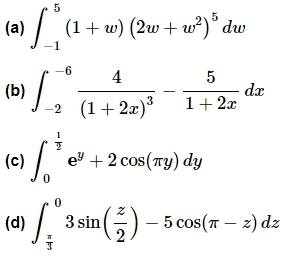
Since we’ve done quite a few substitution rule integrals to this time we aren’t going to put a lot of effort into explaining the substitution part of things here.
Ans: The substitution and converted limits are,
Sometimes a limit will remain the same after the substitution. Don’t get excited when it happens and don’t expect it to happen all the time.
Here is the integral,
Don’t get excited about large numbers for answers here. Sometimes they are. That’s life.
Ans: Here is the substitution and converted limits for this problem,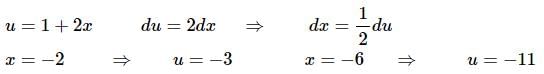
The integral is then,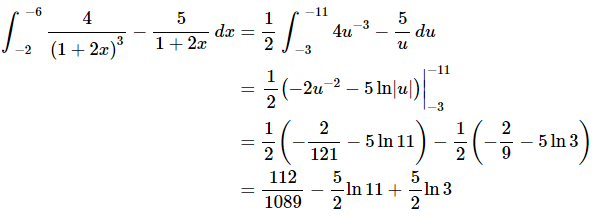
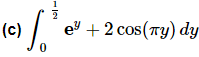
Ans: This integral needs to be split into two integrals since the first term doesn’t require a substitution and the second does.
Here is the substitution and converted limits for the second term.
Here is the integral.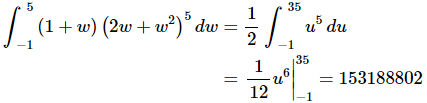
Don’t get excited about large numbers for answers here. Sometimes they are. That’s life.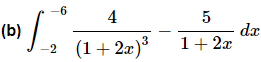
Ans: Here is the substitution and converted limits for this problem,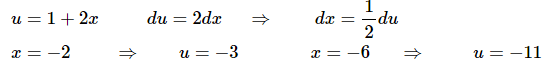
The integral is then,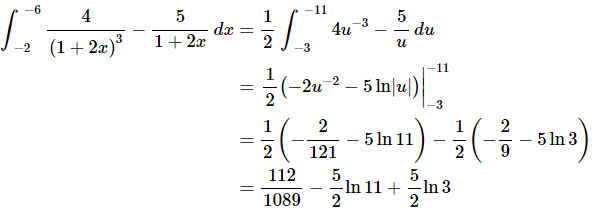
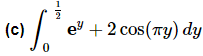
Ans: This integral needs to be split into two integrals since the first term doesn’t require a substitution and the second does.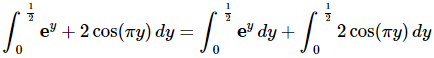
Here is the substitution and converted limits for the second term.
Here is the integral.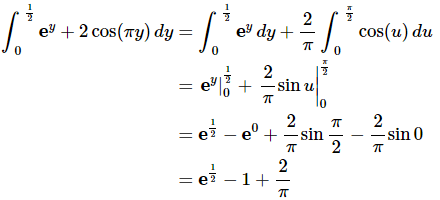
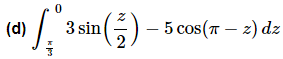
Ans: This integral will require two substitutions. So first split up the integral so we can do a substitution on each term.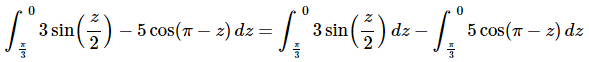
There are the two substitutions for these integrals.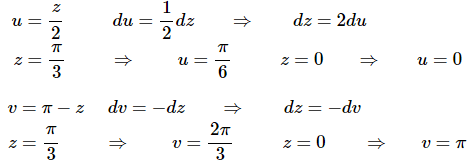
Here is the integral for this problem.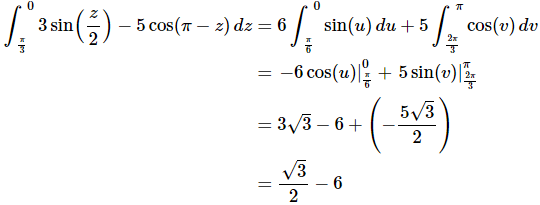
The next set of examples is designed to make sure that we don’t forget about a very important point about definite integrals.
Example 3: Evaluate each of the following.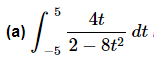
Ans: Be careful with this integral. The denominator is zero at t =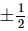 and both of these are in the interval of integration. Therefore, this integrand is not continuous in the interval and so the integral can’t be done.
and both of these are in the interval of integration. Therefore, this integrand is not continuous in the interval and so the integral can’t be done.
Be careful with definite integrals and be on the lookout for division by zero problems. In the previous section they were easy to spot since all the division by zero problems that we had there were where the variable was itself zero. Once we move into substitution problems however they will not always be so easy to spot so make sure that you first take a quick look at the integrand and see if there are any continuity problems with the integrand and if they occur in the interval of integration.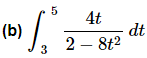
Ans: Now, in this case the integral can be done because the two points of discontinuity,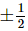 are both outside of the interval of integration. The substitution and converted limits in this case are,
are both outside of the interval of integration. The substitution and converted limits in this case are,
The integral is then,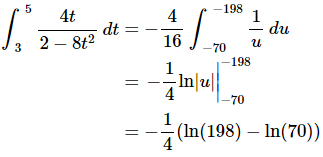
Let’s work another set of examples. These are a little tougher (at least in appearance) than the previous sets.
Example 4: Evaluate each of the following.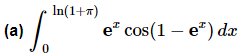
Ans: The limits are a little unusual in this case, but that will happen sometimes so don’t get too excited about it. Here is the substitution.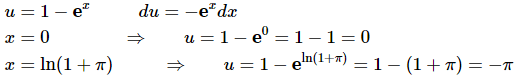
The integral is then,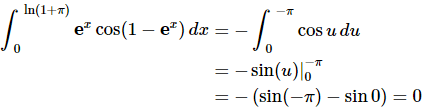
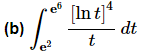
Ans: Here is the substitution and converted limits for this problem.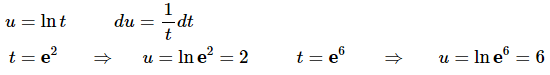
The integral is,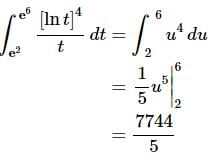
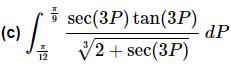
Ans: Here is the substitution and converted limits and don’t get too excited about the substitution. It’s a little messy in the case, but that can happen on occasion.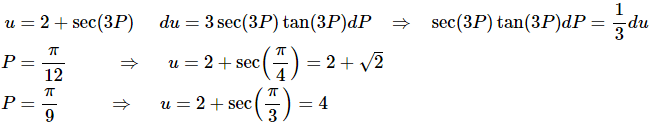
Here is the integral,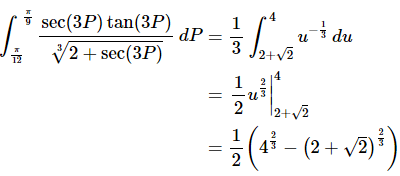
So, not only was the substitution messy, but we also have a messy answer, but again that’s life on occasion.
Ans: This problem not as bad as it looks. Here is the substitution and converted limits.
The cosine in the very front of the integrand will get substituted away in the differential and so this integrand actually simplifies down significantly. Here is the integral.
Don’t get excited about these kinds of answers. On occasion we will end up with trig function evaluations like this.
Ans: This is also a tricky substitution (at least until you see it). Here it is,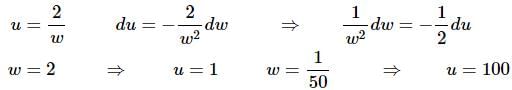
Here is the integral.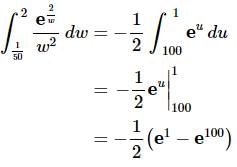
In this last set of examples we saw some tricky substitutions and messy limits, but these are a fact of life with some substitution problems and so we need to be prepared for dealing with them when they happen.
Practice problems: Substitution Rule for Definite Integrals
Q.1. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.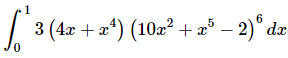
Ans: The first step that we need to do is do the substitution.
At this point you should be fairly comfortable with substitutions. If you are not comfortable with substitutions you should go back to the substitution sections and work some problems there.
The substitution for this problem is,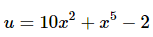
Here is the actual substitution work for this problem.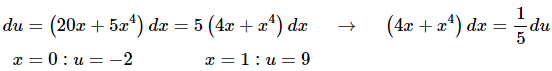
As we did in the notes for this section we are also going to convert the limits to
u’s to avoid having to deal with the back substitution after doing the integral.
Here is the integral after the substitution.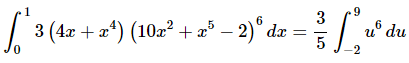
The integral is then,
Do not get excited about “messy” or “large” answers. They will happen on occasion so don’t worry about them when the happen.
Q.2. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.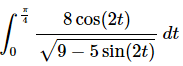
Ans: The first step that we need to do is do the substitution.
At this point you should be fairly comfortable with substitutions. If you are not comfortable with substitutions you should go back to the substitution sections and work some problems there.
The substitution for this problem is,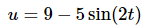
Here is the actual substitution work for this problem.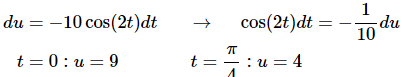
As we did in the notes for this section we are also going to convert the limits to
u’s to avoid having to deal with the back substitution after doing the integral.
Here is the integral after the substitution.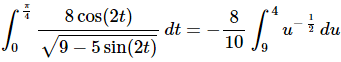
The integral is then,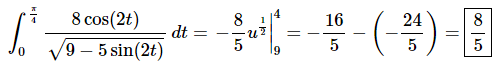
Q.3. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.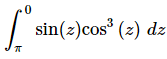
Ans: The first step that we need to do is do the substitution.
At this point you should be fairly comfortable with substitutions. If you are not comfortable with substitutions you should go back to the substitution sections and work some problems there.
The substitution for this problem is,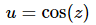
Here is the actual substitution work for this problem.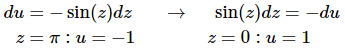
As we did in the notes for this section we are also going to convert the limits to
u’s to avoid having to deal with the back substitution after doing the integral.
Here is the integral after the substitution.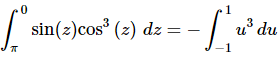
The integral is then,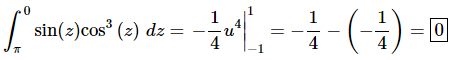
Q.4. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.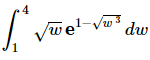
Ans: The first step that we need to do is do the substitution.
At this point you should be fairly comfortable with substitutions. If you are not comfortable with substitutions you should go back to the substitution sections and work some problems there.
The substitution for this problem is,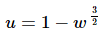
Here is the actual substitution work for this problem.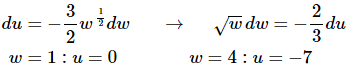
As we did in the notes for this section we are also going to convert the limits to
u’s to avoid having to deal with the back substitution after doing the integral.
Here is the integral after the substitution.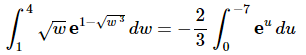
The integral is then,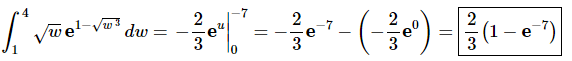
Q.5. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.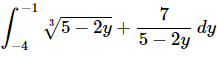
Ans: The first step that we need to do is do the substitution.
At this point you should be fairly comfortable with substitutions. If you are not comfortable with substitutions you should go back to the substitution sections and work some problems there.
The substitution for this problem is,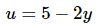
Here is the actual substitution work for this problem.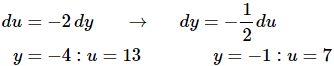
As we did in the notes for this section we are also going to convert the limits to
u’s to avoid having to deal with the back substitution after doing the integral.
Here is the integral after the substitution.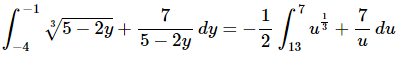
The integral is then,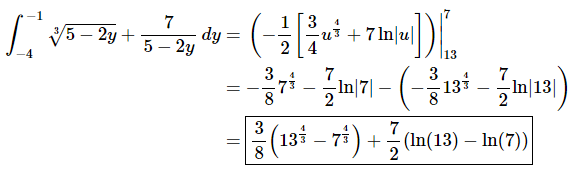
Q.6. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.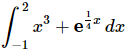
Ans: The first step that we need to do is do the substitution.
At this point you should be fairly comfortable with substitutions. If you are not comfortable with substitutions you should go back to the substitution sections and work some problems there.
Before setting up the substitution we’ll need to break up the integral because the first term doesn’t need a substitution. Doing this gives,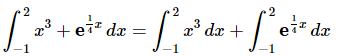
The substitution for the second integral is then,
Here is the actual substitution work for this second integral.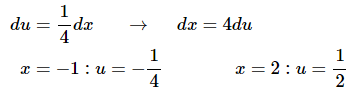
As we did in the notes for this section we are also going to convert the limits to
u’s to avoid having to deal with the back substitution after doing the integral.
Here is the integral after the substitution.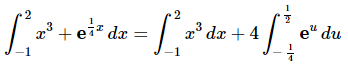
The integral is then,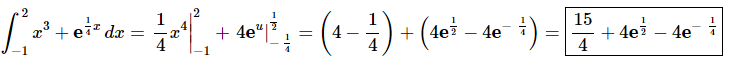
Q.7. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.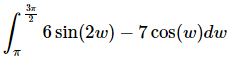
Ans: The first step that we need to do is do the substitution.
At this point you should be fairly comfortable with substitutions. If you are not comfortable with substitutions you should go back to the substitution sections and work some problems there.
Before setting up the substitution we’ll need to break up the integral because the second term doesn’t need a substitution. Doing this gives,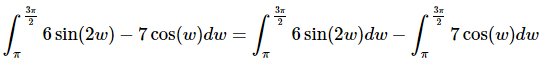
The substitution for the first integral is then,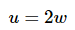
Here is the actual substitution work for this first integral.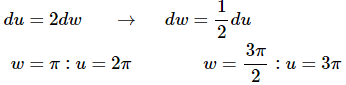
As we did in the notes for this section we are also going to convert the limits to
u’s to avoid having to deal with the back substitution after doing the integral.
Here is the integral after the substitution.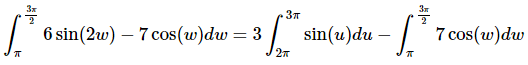
The integral is then,
Q.8. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.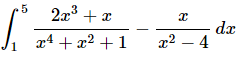
Ans: Be very careful with this problem. Recall that we can only do definite integrals if the integrand (i.e. the function we are integrating) is continuous on the interval over which we are integrating.
In this case the second term has division by zero at x = 2 and so is not continuous on [1,5] and therefore this integral can’t be done.
Q.9. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.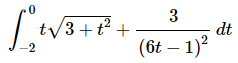
Ans: The first step that we need to do is do the substitution.
At this point you should be fairly comfortable with substitutions. If you are not comfortable with substitutions you should go back to the substitution sections and work some problems there.
Before setting up the substitution we’ll need to break up the integral because each term requires a different substitution. Doing this gives,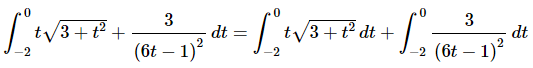
The substitution for each integral is then,
Here is the actual substitution work for this first integral.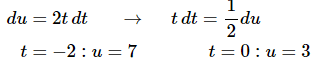
Here is the actual substitution work for the second integral.
As we did in the notes for this section we are also going to convert the limits to
u’s to avoid having to deal with the back substitution after doing the integral.
Here is the integral after the substitution.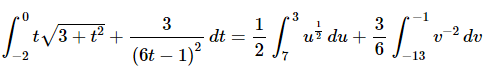
The integral is then,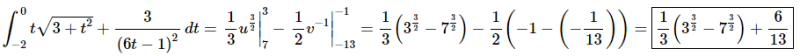
Q.10. Evaluate the following integral, if possible. If it is not possible clearly explain why it is not possible to evaluate the integral.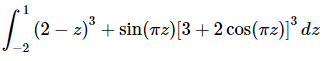
Ans: The first step that we need to do is do the substitution.
At this point you should be fairly comfortable with substitutions. If you are not comfortable with substitutions you should go back to the substitution sections and work some problems there.
Before setting up the substitution we’ll need to break up the integral because each term requires a different substitution. Doing this gives,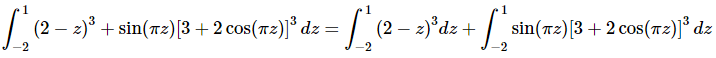
The substitution for each integral is then,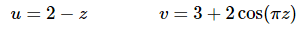
Here is the actual substitution work for this first integral.
Here is the actual substitution work for the second integral.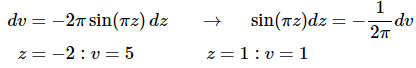
As we did in the notes for this section we are also going to convert the limits to
u’s to avoid having to deal with the back substitution after doing the integral.
Here is the integral after the substitution.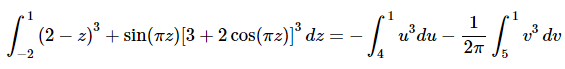
The integral is then,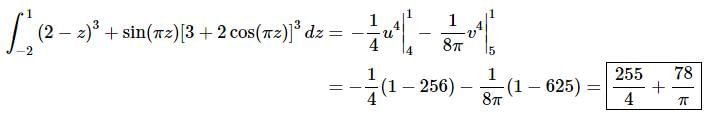
|
112 videos|65 docs|3 tests
|
FAQs on Substitution Rule for Definite Integrals - Calculus - Mathematics
| 1. What is the substitution rule for definite integrals? |  |
| 2. How does the substitution rule work for definite integrals? |  |
| 3. What are the steps involved in using the substitution rule for definite integrals? |  |
| 4. What are some common substitutions used in the substitution rule for definite integrals? |  |
| 5. Can the substitution rule be used for all definite integrals? |  |
















