Probability Summary | Quantitative Aptitude for CA Foundation PDF Download
SUMMARY
Experiment: An experiment may be described as a performance that produces certain results.
Random Experiment: An experiment is defined to be random if the results of the experiment depend on chance only.
Events: The results or outcomes of a random experiment are known as events. Sometimes events may be combination of outcomes. The events are of two types:
(i) Simple or Elementary,
(ii) Composite or Compound.
Mutually Exclusive Events or Incompatible Events: A set of events A1, A2, A3, …… is known to be mutually exclusive if not more than one of them can occur simultaneously
Exhaustive Events: The events A1, A2, A3, ………… are known to form an exhaustive set if one of these events must necessarily occur.
Equally Likely Events or Mutually Symmetric Events or Equi-Probable Events: The events of a random experiment are known to be equally likely when all necessary evidence are taken into account, no event is expected to occur more frequently as compared to the other events of the set of events.
The probability of occurrence of the event A is defined as the ratio of the number of events favourable to A to the total number of events. Denoting this by P(A), we have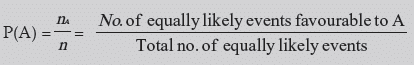
(a) The probability of an event lies between 0 and 1, both inclusive.

When P(A) = 0, A is known to be an impossible event and when P(A) = 1, A is known to be a sure event.
(b) Non-occurrence of event A is denoted by A’ or AC or 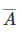 and it is known as complimentary event of A. The event A along with its complimentary A’ forms a set of mutually exclusive and exhaustive events.
and it is known as complimentary event of A. The event A along with its complimentary A’ forms a set of mutually exclusive and exhaustive events.

(c) The ratio of no. of favourable events to the no. of unfavourable events is known as odds in favour of the event A and its inverse ratio is known as odds against the event A.
i.e. odds in favour of A = mA : (m – mA)
and odds against A = (m – mA) : mA
(d) For any two mutually exclusive events A and B, the probability that either A or B occurs is given by the sum of individual probabilities of A and B.
i.e. P (A∪ B)
or P(A + B) = P(A) + P(B)
(e) For any K( ≥ 2) mutually exclusive events A1, A2, A3 …, AK the probability that at least one of them occurs is given by the sum of the individual probabilities of the K events.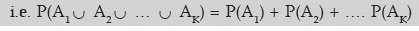
|
101 videos|209 docs|89 tests
|
FAQs on Probability Summary - Quantitative Aptitude for CA Foundation
| 1. What is Probability? |  |
| 2. How is probability calculated? |  |
| 3. What is the difference between independent and dependent events in probability? |  |
| 4. How is probability used in real-life situations? |  |
| 5. What are the applications of probability in business and economics? |  |

















