ICAI Notes- Syllogism | Quantitative Aptitude for CA Foundation PDF Download
INTRODUCTION
Syllogism is a ‘Greek’ word that means inference or deduction. As such inferences are based on logic, then these inferences are called logical deduction. These deductions are based on propositions (premise).
Different types of questions covered in this chapter are as follows:
- Two Statements and Two Conclusions
‘Syllogism’ checks basic aptitude and ability of a candidate to derive inferences from given statements using step by step methods of solving problems.
Proposition
Let us consider the following sentences:
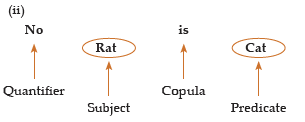
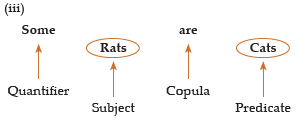

In all the sentences mentioned above, a relation is established between subject and predicate with the help of quantifier and copula.
Now, we can define proposition as under:
A proposition or premise is grammatical sentence comprising of four components.
- Quantifier
- Subject
- Copula
- Predicate
Quantifier– The words ‘All’ ‘No’ and ‘Some’ are called quantifiers as they specify a quantity. Keep in mind that ‘All’ and ‘No’ are universal quantifiers because they refer to each and every object of a certain set.
‘Some’ is a particular quantifier as it refers to at least one existing object in a certain set.
Subject– Subject is the part of the sentence something is said about. It is denoted by S.
Copula– It is that part of a proposition that denotes the relation between subject and predicate.
Predicate– It is that part of a proposition which is affirmed detail about that subject.
Classification of Proposition
A proposition can mainly be divided into three categories.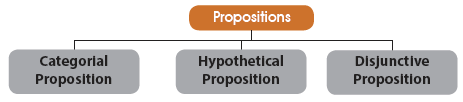
(i) Categorical Proposition: In categorical proposition, there exists a relationship between the subject and the predicate without any condition. It means predicate is either affi rmation or denial of the subject unconditionally.
Example: I. All cups are pens.
II. No boy is girl.
(ii) Hypothetical Proposition: In a hypothetical proposition, relationship between subject and predicate is asserted conditionally.
Example: I. If it rains, he will not come.
II. If he comes, I will accompany him.
(iii) Disjunctive Proposition: In a disjunctive proposition, the assertion is of alteration.
Example: I. Either he is sincere or he is loyal.
II. Either he is educated or he is scholar.
Keeping in view with the existing pattern of Syllogism in competitive examinations, we are concerned only with the categorical type of proposition.
Venn Diagram Representation of Two Propositions
Types of Venn diagram can be understood by the following diagram: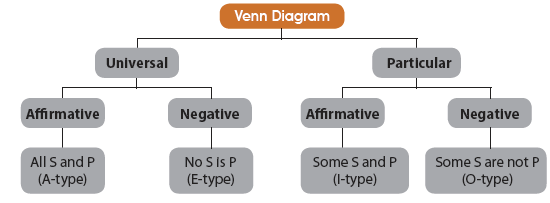
From the above diagram, following things are very much clear:
(i) Universal propositions, Either
(a) completely include the subject (A-type)
or
(b) completely exclude the subject (E-type)
(ii) Particular propositions, Either
(a) partly include the subject (I-type)
or
(b) partly exclude the subject (O-type)
Now, we can summarize the four standard types of propositions (premises) as below:
| Format | Type |
| All S are P (Universal Affirmative) | A |
| No S is P (Universal Negative) | E |
| Some S are P (Particular Afirmative) | I |
| Some S are not P (Particular Negative) | O |
Venn Diagram Representation
(i) A-Type (All S are P)
(ii) E-Type (No S is P)
(iii) E Type (No S is P)
(iv) O Type (Some S are not P)
Hidden Propositions
The type of propositions we have discussed earlier are of standard nature but there are propositions which do not appear in standard format and yet can be classified under any of the four types.
Let us now discuss the type of such propositions.
I. A-Type Propositions
(i) All positive propositions beginning with ‘every’ and ‘any’ are A type propositions.
Example:
(a) Every cat is dog ⇒ All dogs are cats
(b) Each of students of class has passed ⇒ All students of class X have passed
(c) Anyone can do this job ⇒ All (Women) can do this job
(ii) A positive sentence with a particular person as its subject is always an A-type proposition.
Example:
(a)
(b)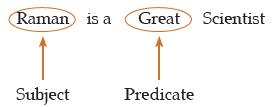
(iii) A sentence with a definite exception is A type.
Example: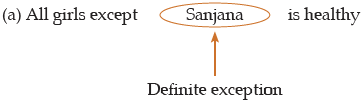
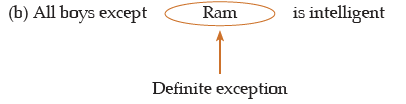
II. E-Type Propositions
(i) All negative sentences beginning with ‘no one’, ‘not a single’ etc., are E-type propositions.
Example:
(a) Not a single student could answer the question.
(b) None can cross the English channel.
(ii) A negative sentence with a very definite exception is also of E-type proposition.
Example: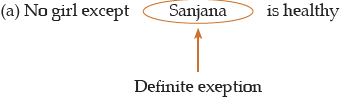
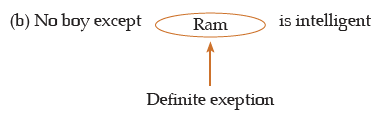
(iii) When an Introgattive sentence is used to make an assertion, this could be reduced to an E-type proposition. example: Is there any person who can scale Mount Everest? ⇒ Non can climb Mount Everest.
(iv) A negative sentence with a particular person as its subject is E-type proposition.

III. I-Type Propositions
(i) Positive propositions beginning with words such as ‘most’, ‘a few’ ‘mostly’, ‘generally’, ‘almost’, ‘frequently’, and ‘often’ are to be reduced to the I-type propositions.
Example:
(a) Almost all the Vegetables have been sold. ⇒ Some vegetables have been sold.
(b) Most of the students will qualify in the test. ⇒ Some of the students will qualify in
the test.
(c) Boys are frequently physically weak ⇒ Some boys are physically weak.
(ii) Negative propositions beginning with words such as ‘few’ ‘seldom’, ‘hardly’, ‘rarely’, ‘little’ etc. are to be reduced to the I-type propositions.
Example:
(a) Seldom writers do not take rest. ⇒ Some writers take rest.
(b) Few Teachers do not tell a lie. ⇒ Some teachers tell a lie.
(c) Rarely Scientists do not get a good job ⇒ Some Scientists get a good job.
(iii) A positive sentence with an exception which is not de⇒ nite, is reduced to an I-type proposition.
Example: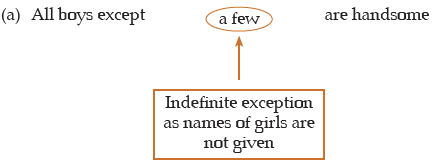
IV. O-Type Propositions
(i) All negative propositions beginning with words such as ‘all’, ‘every’, ‘any’, ‘each’ etc. are to be reduced to O-type propositions.
Example:
(a) All Psychos are not guilty. ⇒ Some Physchos are not guilty.
(b) All that glitters is not gold. ⇒ Some glittering objects are not gold.
(c) Everyone is not Scientist ⇒ Some are not Scientist.
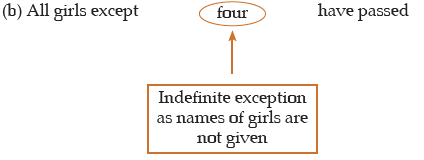
(ii) Negative propositions with words as ‘most’, ‘a few’, ‘mostly, ‘generally’, ‘almost’, ‘frequently’ are to be reduced to the O-type propositions.
Example:
(a) Boys are usually not physically weak. ⇒ Some boys are not physically weak.
(b) Priests are not frequently thiefs. ⇒ Some priests are not thiefs.
(c) Almost all the questions cannot be solved. ⇒ Some questions cannot be solved.
(iii) Positive propositions with starting words such as ‘few’, ‘seldom’, ‘hardly’, ‘scarcely’, ‘rarely’, ‘little’, etc., are to be reduced to the O-type propositions.
Example:
(a) Few boys are intelligent. ⇒ Some boys are not intelligent
(b) Seldom are innocents guilty. ⇒ Some innocent are not guilty.
(iv) A negative sentence with an exception, which is not definite is to be reduced to the O-type propositions.
e.g.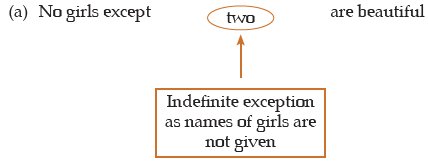

Exclusive Propositions
Such propositions start with ‘only’, ‘alone’, ‘none but’, ‘none else but’ etc., and they can be reduced to either A or E or l-type.
Example:
Only Post-graduates are officers. (E-type)
None Post-graduate is officer. (A-type)
All officers are Post-graduates. (I-type)
Some Post-graduates are officers
Types of Inferences
Inferences drawn from statements can be of two types:
1. Immediate Inference: When an inference is drawn from a single statement, then that inference is known as an immediate inference.
Example: Statement: All books are pens.
Conclusion: Some pens are books.
In the above example, a conclusion is drawn from a single statement and does not require the second statement to be referred, hence the inference is called an immediate inference.
2. Mediate Inference: In mediate inference, conclusion is drawn from two given statements.
Example: Statements: All cats are dogs.
All dogs are black.
Conclusion: All cats are black.
In the above example, conclusion is drawn from the two statements or in other words, both the statements are required to draw the conclusion. Hence, the above conclusion is known as mediate inference.
Method to Draw Immediate Inferences
There are various methods to draw immediate inferences like conversion, obversion, contraposition; etc. Keeping in view the nature of questions asked in various competitive examinations, we are required to study only two methods, implications and conversion.
(i) Implications (of a given proposition): Below we shall discuss the implications of all the four types of propositions. While drawing a conclusion through implication, subject remains the subject and predicate remains the predicate.
A-Type: All boys are blue.
From the above A-type proposition, it is very ‘clear that if all boys are blue, then some boys will definitely be blue because some is a part of all. Hence, from A-type proposition, we can draw l-type conclusion (through implication).
E-Type: No cars are buses.
If no’ cars are buses, it clearly means that some cars are not buses. Hence, from E-type proposition, O-type conclusion (through implication) can be drawn.
I-Type: Some chairs are tables.
‘From the above l-type proposition, we cannot draw any valid conclusion (through implication).
O-Type: Some A are not B.
From the above O-type proposition, we can not draw any valid inference (through implication). On first look, it appears that if some A are not B, then conclusion that some A are B must be true but the possibility of this conclusion being true can be over ruled with the help of following example:
Case I A = {a, b, c} and B = {d, e, f}
Case II A = {a, b, c} and B ={b, c, d}
The above two cases show the relationship between A and B given by O-type proposition. “Some A are not B”. Now, in case I, none of the element of set A is the element of set B. Hence, conclusion “Some A are B” cannot be valid. However, in case II, elements b and c are common to both sets A and B. Hence, here conclusion “Some A are B” is valid. But for any conclusion to be true, it should be true for all the cases. Hence, conclusion “Some A are B” is not a valid conclusion drawn from an O-type proposition.
All the results derived for immediate inference through implication can be presented in the table as below:
Conversion: Conversion is other way of getting immediate inferences. Unlike implication, in case of conversion, subject becomes predicate and predicate becomes subject. Let us see
Conversion of A-type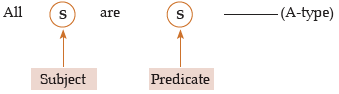
After conversion it becomes
Clearly, A gets converted into I-type.
Conversion of E-type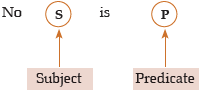
After conversion it becomes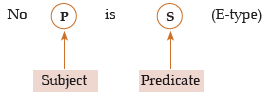
Clearly, E gets converted into E-type.
Conversion of I-type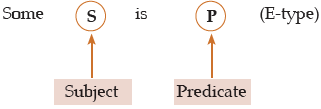
Clearly I gets converted into I- type.
Conversion of O – type.
O type propositions cannot be converted.
Now we can make a conversion as follows: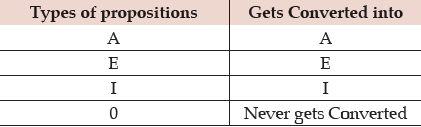
Immediate Inference Table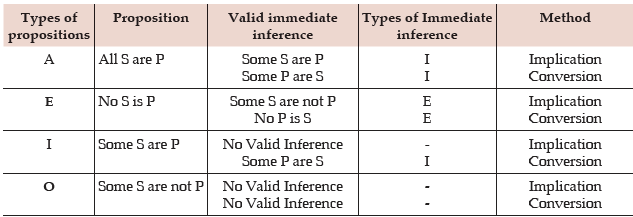
Venn Diagram Representation of Immediate Inferences:
Immediate inferences are drawn from each type of Propositions (A, E, I , O)
1) A type All S are P
(i) S = { a, b, c } , P = { a, b, c, d, e}
(i) S = { a, b, c} , P = { a, b, c, d, e, f}
(ii) S = { a, b, c} , P = { a, b, c}
The above cases show all the possibilities of two sets S and P showing the relationship by the proposition.
All S are P in both cases.
Some S are P.(Is true from relationship)
Some P are S (Its true)
Some P are not S is not valid because from it is case (i) but false from case (ii)
Inference All (P are S ) is not valid because its true from case (ii) and False from case (i)
2) E type – No S Is P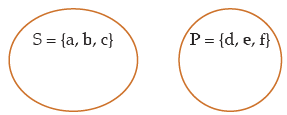
We can draw the inferences as
(i) No P is S
(ii) Some S are not P
(iii) Some P are not S
Any other inference drawn from E- type proposition is not valid.
3) I-type: Some S are P
(i) S = { a, b, c, d} , P = {c, d, e, f}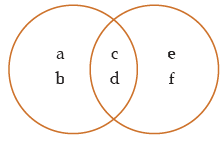
Some S are P
(ii) S = { a, b, c, d} and P = { a, b}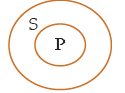
Set {a, b} is the part of S as well as Set P, hence some set S are P.
(iii) S = {a, b} , P = {a, b, c, d}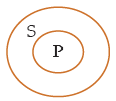
Set {b} is the part of the set S as well as Set P, hence some S are P.
(iv) S = {a, b, c} , P = {a, b, c}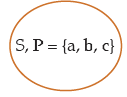
The above diagrams show the relationship between S and P from I-type relationship. From the possible combinations, it’s clear that inference (Some P are S) is true. Inference (S are not P) is true from combinations (i) and (ii) but is not true from combinations (iii) and (iv). Therefore inference (Some S are not P) is not a valid inference drawn from the above proposition.
Set {a, b} is part of set S and P, hence some s are P.
4) O-Type: Some S are not P
(i) S = {a, b, c, d} , P = {c, d, e, f}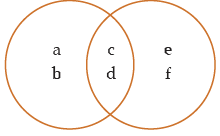
Set {a, b} is part of the set S but not Set P
Hence Some S are not P
(ii) S= {a, b, c} and P = {d, e, f}
Set {a, b} is the part of S but not set P
Hence the above relation represented by Some S are not P .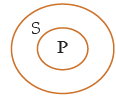
(iii) S = {a, b, c, d, e, f} , P = {e,f}
Set {a, b, c} is the part of set S abut not P. Hence Proposition Some S are not P.
On the basis of all possible combinations showing relationship between S and P, no valid inference can be drawn. Inference from Some P are not S) is true combination (i) and (iii) but not true for combination (iii). Hence it is invalid inference.
Inference (Some P are not S) is true from combination (i) and (ii) but not true for combination (iii), hence it is also invalid.
Following are the main rules for solving syllogism problems.
1) All + All = All
2) All + No = No
3) All + Some = No conclusion
4) Some + No = Some Not
5) Some + Some = No conclusion
6) No + All = Some not (Reversed)
7) No + All = Some Not (Reversed)
8) No + Some = Some Not (Reserved)
9) No + No = No conclusion
10) Some Not/ Some not reserved + Anything = No conclusion
11) If all A are B then we can say – Some B are Not A is a possibility
12) If Some B are not A then we can say – All A are B is a possibility
13) If some A are B then we can say All A are B is a possibility. All B are A is a possibility.
14) All ⇔ Some not reserved
15) Some ⇔ All
16) No conclusion = Any possibility is true
Implications (In case of Conclusions from Single Statement)
All ⇔ Some That means If A are B then Some B is true.
Some ⇔ Some that means if Some A are B then Some B are A is true.
No ⇔ No that means if No A is B then No B is true.
Examples:
In this type of questions two statements and two conclusions are given. Its required to check.
Example 1:
Statement:
I. Some boys are student.
II. All students are Engineers.
Conclusions:
I. All Engineers are students.
II. Some boys are Engineers.
(a) Only I follows
(b) Only II follows
(c) Both I and II follow
(d) Neither I nor II follows.
Solution
(b) Statement I is an I-type proposition which distributes neither the subject nor the predicate.
Statement II is an A-type propositions which distributes the subject ‘Engineers’ only.
Since, the Engineers is distributed in Conclusion I without being distributed in the premises. So, Conclusion I cannot follow. In second conclusion, where it is asked that some boys are Engineers but from Statement I nit is clear that some boys are not students. These boys may not be Engineers.
Example 2:
Statements:
I. All Lotus are flowers.
II. No Lily is a Lotus.
Conclusions:
I. No Lily is a flower
II. Some Lilies are flowers.
(a) Only I follows
(b) Only II follows
(c) Either I or II follows
(d) Neither I nor II follows
Solution: (c)
Here, the first premise is an A-type proposition and so the middle term ‘Lotus’ forming the subject is distributed. The second premise is an E proposition and so the middle term ‘Lotus’ forming the predicate is distributed. Since, the middle term is distributed twice, so the conclusion cannot be universal.
Example 3:
Statements
I All A’s are C’s
II All D’s are C’s
Conclusion
I All D’s are C’s
II. Some D’s are not A’s
(a) Only I follows
(b) Only II follows
(c) Both I and II follows
(d) None follows
Solution: (a) Now, taking conclusion I, it is clear that all D’s are also C’s but taking conclusion II, we cannot say that some D’s are not A’s because from Statement I it is clear that all D’s are A’s. Hence, only Conclusion I follows.
Example 4:
Statements: All balls are bats.
All bats are stumps.
The sentences are already aligned. From the above given Table, A + A = A. Hence the conclusion is of type-A whose subject is the subject of the first proposition and the predicate is the predicate of the second proposition?
So the conclusion is All balls are Stumps.
Example 5:
Statements: All Professors are readers.
All Professors are writers.
This pair is not properly aligned because the subject of both the sentences is ‘Professors’.
Since both the sentences are of type-A, we may convert any of them. So the aligned pair is Some readers are Professors.
All Professors are writers.
Here the conclusion will be of type - I
because I + A = I.
The conclusion is Some readers are writers.
Example 6:
Statements: Some Mangos are sweets.
All Mangos are Fruits.
The subject of both the sentences is the same. By the rule of IEA, we convert the
I - type statement. So the aligned pair is,
Some Sweets are Mangos.
All Mangos are Fruits
I+A=I. So the conclusion is
Some Sweets are Fruits.
Example 7:
Statements: All lights are bats.
No balls are lights.
By changing the order of the statements itself.
We can align the sentences. The aligned pair is
No balls are lights.
All lights are bats.
E + A = O*.
So the conclusion is,
Some bats are not balls.
Example 8: Statements: Some caps are blue.
No clip is blue.
Here the common term is ‘blue’ which is the predicate of both the sentences. By the rule of IEA, we convert the I-type statement. After conversion, the given pair becomes,
Some blue are caps.
No clip is blue.
Now by changing the order of the statements, we can align the sentences. So the aligned pair is, No clip is blue.
Some blue are caps.
The conclusion is of type O* since, E + I = O*. Hence the conclusion is Some caps are not clips.
Example 9:
Statements: Some powders are not soaps.
All soaps are detergents.
The given pair is properly aligned. But no definite conclusion can be drawn from this type because it is a O+A - type combination.
Complementary Pair
Consider the following.
Conclusions:
i) Some vans are trucks.
ii) Some vans are not trucks.
We know that either some vans will be trucks or some vans will not be trucks.
Hence either (i) or (ii) is true. Such pair of statements are called complementary pairs. So in a complementary pair, at least one of the two statements is always true. We can call a pairs a complementary pair if i) The subject and predicate of both the sentences are the same.
ii) They are an I + O - type pair or an A + O type pair or an I + E - type pair.
Some complementary pairs are given below.
i) All birds are Pigeons.
Some birds are not Pigeons.
ii) Some Chairs are watches.
Some Chairs are not watches.
iii) Some kids are cute.
No kids are cute.
Note: The steps to be followed to do a syllogism problem by analytical method are mentioned below.
i) Align the sentences properly.
ii) Draw conclusion using the table.
iii) Check for immediate inferences.
iv) Check for complementary pair if steps ii and iii fail.
|
115 videos|174 docs|98 tests
|
FAQs on ICAI Notes- Syllogism - Quantitative Aptitude for CA Foundation
| 1. What is the significance of syllogism in the CA Foundation exam? |  |
| 2. How can I prepare for the syllogism section in the CA Foundation exam? |  |
| 3. Are there any shortcuts or tricks to solve syllogism questions quickly in the CA Foundation exam? |  |
| 4. Can I expect direct syllogism questions in the CA Foundation exam? |  |
| 5. Are there any recommended study materials or resources for syllogism preparation for the CA Foundation exam? |  |
|
115 videos|174 docs|98 tests
|

|
Explore Courses for CA Foundation exam
|

|


















