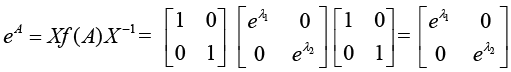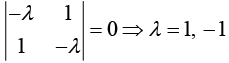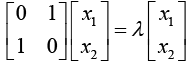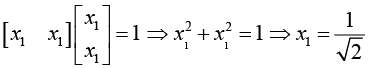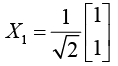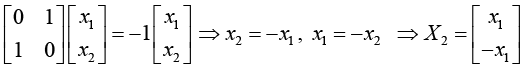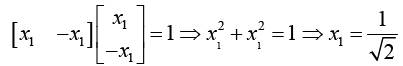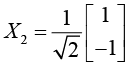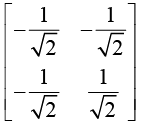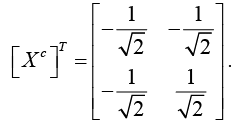Symmetric, Skew-Symmetric, Orthogonal & Complex Matrices | Mathematical Methods - Physics PDF Download
Symmetric Matrix
A real square matrix A = [aij] is called symmetric if transposition leaves it unchanged,
AT = A thus aij = aji .
The Eigen-values of symmetric matrix are always real.
Example: 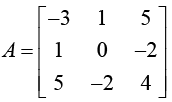
Skew-Symmetric Matrix
A real square matrix A = [aij] is called skew-symmetric if transposition gives the negative of A,
AT = - A thus aij = -aji
Every skew-symmetric matrix has all main diagonal entries zero.
The Eigen-values of skew-symmetric matrix are pure imaginary or zero.
Example : 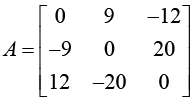
NOTE:
Any real square matrix A may be written as the sum of a symmetric matrix R and a skew-symmetric matrix S, where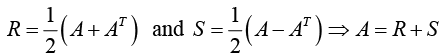
Example: 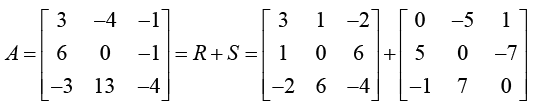
Orthogonal Matrix
A real square matrix A =[aij] is called orthogonal if transposition gives the inverse of A,
AT = A-1
NOTE:
(i) A real square matrix is orthogonal if and only if its column vectors and also its row vectors form an orthonormal system, that is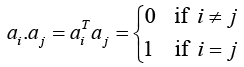
Thus ATA = I
(ii) The determinate of an orthogonal matrix has the value +1 or -1.
(iii) The eigenvalues of an orthogonal matrix A are real or complex conjugate in pairs and have absolute value 1.
Example: 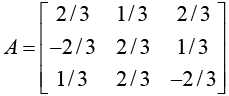
Its characteristic equation is 
Hermitian, Skew-Hermitian, and Unitary Matrices (Complex Matrices)
The complex conjugate of an matrix A is formed by taking the complex conjugate of each element. Thus 
For the conjugate transpose, we use the notation 
Example: 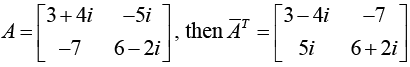
Hermitian Matrix
A square matrix A = [aij] is called Hermitian if
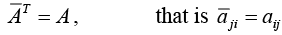
If A is Hermitian, the entries on the main diagonal must satisfy 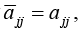 that is they are real.
that is they are real.
If a Hermitian matrix is real, then 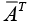 = AT = A. Hence a real Hermitian matrix is a symmetric matrix.
= AT = A. Hence a real Hermitian matrix is a symmetric matrix.
The eigenvalues of a Hermitian matrix (and thus a symmetric matrix) are real.
Example:  The eigenvalues are 9, 2 .
The eigenvalues are 9, 2 .
Skew- Hermitian Matrix
A square matrix A = [aij] is called skew-Hermitian if

- If A is skew-Hermitian, then entries on the main diagonal must satisfy

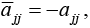 hence ajj must be pure imaginary or 0.
hence ajj must be pure imaginary or 0. - If a skew-Hermitian matrix is real, then
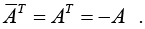 Hence a real skew-Hermitian matrix is a skew-symmetric matrix.
Hence a real skew-Hermitian matrix is a skew-symmetric matrix. - The eigenvalues of a skew-Hermitian matrix (and thus a skew-symmetric matrix) are pure imaginary or 0.
Example:
The eigenvalues are 4i, - 2i.
Unitary Matrix
A square matrix A = [aij] is called unitary if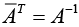
- If a unitary matrix is real, then
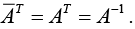 Hence a real unitary matrix is an orthogonal matrix.
Hence a real unitary matrix is an orthogonal matrix. - The eigenvalues of a unitary matrix (and thus an orthogonal matrix) have absolute value 1.
Example: 
The eigenvalues are 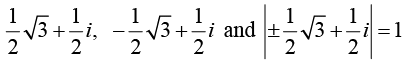
Similarity of Matrices, Basis of Eigenvectors, and Diagonalisation
Eigenvectors of an n x n matrix A may (or may not) form a basis. If they do, we can use them for “diagonalizing” A , that is, for transforming it into diagonal form with the eigenvalues on the main diagonal.
Similarity of Matrices
An n x n matrix  is called similar to an n x n matrix A if
 = P-1AP
For some (nonsingular) n x n matrix P . This transformation, which gives  from A , is called similarity transformation.
- If  is similar to A, then  has the same eigenvalues as A .
- If x is an eigenvector of A, then y = P-1x is an eigenvector of  corresponding to same eigenvalue.
- If λ1,λ2,....λk be distinct eigenvalues of an n x n matrix. Then corresponding eigenvectors x1,x2,....xk form linearly independent set.
Basis of Eigenvectors
If an n x n matrix A has n distinct eigenvalues, then A has a basis of eigenvectors
- A Hermitian, skew-Hermitian or unitary matrix has a basis of eigenvectors.
- A symmetric matrix has an orthonormal basis of eigenvectors.
Diagonalisation
If an n x n matrix A has a basis of eigenvectors, then
D = X-1 AX
is diagonal, with the eigenvalues of A as the entries on the main diagonal. Here X is the matrix with these eigenvectors as column vectors. Also
Dm = X-1 AmX
A square matrix which is not diagonalizable is called defective.
Example: A = 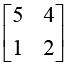 has eigenvalues 6, 1. The corresponding eigenvectors are
has eigenvalues 6, 1. The corresponding eigenvectors are 

Thus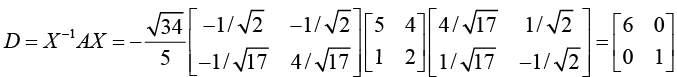
Example: A = 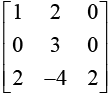 has eigenvalues λ1 =3,λ2,=2,λ1 =1.
has eigenvalues λ1 =3,λ2,=2,λ1 =1.
The eigenvectors of A corresponds to eigen value respectively λ1 = 3. λ2 = 2. λ1 = 1 are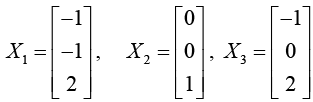
Now, let X be the matrix with these eigenvectors as its columns: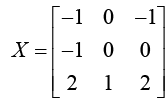
Note there is no preferred order of the eigenvectors inX; changing the order of the eigenvectors in X just changes the order of the eigenvalues in the diagonalzed form of A.
Thus, D = X-1 AX = 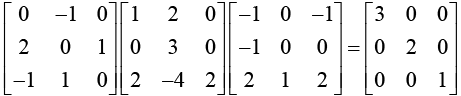
Note that the eigenvalues λ1, = 3, λ2 = 2, λ1 = 1 appear in the diagonal matrix.
Functional Matrices
If the matrix A is diagonalizable, then we can find a matrix X and a diagonal matrix D such that
D = X-1 AX ⇒ A = XDX-1 and An = XDnX-1
Applying the power series definition to this decomposition, we find that f (A) is defined
by
f (A) = I + α A + βA2 + y A3 + (a, β,y are coefficient of Taylor Expansion)
⇒ f (A) = XIX-1 + aXDX-1 + βXD2X-1 + γXD3X-1 +....... ∵ An = XDnX-1
⇒ f (A) = X [I + αD + βD2 + yD3 + ........] X-1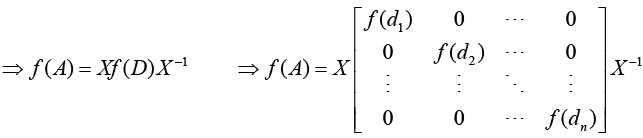
where d1, d2, dn denote the diagonal entries of D.
Note: If A is itself diagonal then f (A) = f (D)
Example 10: If matrix 
For matrix A Eigenvalues are λ1,λ2 and Eigenvectors are respectively
Thus
Example: If matrix 
then 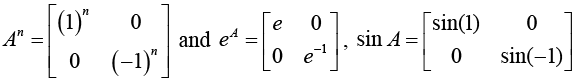
Example 11: If matrix A =  then find eA .
then find eA .
For eigenvalues (A - λI) = 0 ⇒
Eigenvector can be determined by the equation AX = λX .
For λ1 = 1
Normalized eigenvector can be determined by relation X1TX1 = 1
Normalized Eigenvector corresponds to λ1 = 1 is
For λ2 = -1
Normalized eigenvector can be determined by relation X2TX2 = 1.
Normalized Eigenvector corresponds to λ2 = -1 is
Hence,The cofactor of X is Xc =
Hence
NOTE: Always try to express X as unitary matrix because its inverse is same. If X is not unitary matrix then we have to find its inverse.
Thus,
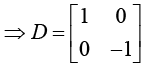


|
78 videos|18 docs|24 tests
|
FAQs on Symmetric, Skew-Symmetric, Orthogonal & Complex Matrices - Mathematical Methods - Physics
| 1. What is the difference between a Hermitian and a Skew-Hermitian matrix? |  |
| 2. What are the properties of a Unitary matrix? |  |
| 3. How do you determine if two matrices are similar? |  |
| 4. What is the significance of a basis of eigenvectors in diagonalizing a matrix? |  |
| 5. What are the properties of Symmetric, Skew-Symmetric, Orthogonal, and Complex matrices? |  |