System and Conservation of Mass - Civil Engineering (CE) PDF Download

System 
We define a system as a particular collection of matter or a particular region of space. The complement of a system, i.e., the matter or region outside the system, is called the surroundings. The surface that separates the system from its surroundings is called the boundary or wall of the system.
A closed system consists of a fixed amount of matter in a region Ω in space with boundary surface ∂Ω which depends on time t. While no matter can cross the boundary of a closed system, energy in the form of work or heat can cross the boundary. The volume of a closed system is not necessarily fixed. If the energy does not cross the boundary of the system, then we say that the boundary is insulated and such a system is said to be mechanically and thermally isolated. An isolated system is an idealization for no physical system is truly isolated, for there are always electromagnetic radiation into and out of the system.
An open system (or control volume) focuses in on a region in space, Ωc which is independent of time t. The enclosing boundary of the open system, over which both matter and energy can cross is called a control surface, which we denote by ∂Ωc.

Conservation of Mass 
At the intuitive level mass is perceived to be a measure of the amount of material contained in an arbitrary portion of the body. As such it is a nonnegative scalar quantity independent of time and not generally determined by the size of the configuration occupied by the arbitrary sub-body. It is not a count of the number of material particles in the body or its sub-parts. However, the mass of a body is the sum of the masses of its parts. These statements can be formalized mathematically by characterizing mass as a set function with certain properties and we proceed on the basis of the following definitions.
Let B_t be an arbitrary configuration of a body B and let A be a set of points in B_t occupied by the particles in an arbitrary subset A of B. If with A there is associated a non-negative real number m(A) having a physical dimension independent of time and distance and such that
(i) m(A₁ ∪ A₂) = m(A₁) + m(A₂) for all pairs A₁, A₂ of disjoint subsets of B, and
(ii) m(A) → 0 as volume of A tends to zero,

B is said to be a material body with mass function m. The mass content of A, denoted by m(A), is identified with the mass m(A) of A. Property two is a consequence of our assumption that the body is a continuum, precluding the presence of point masses. Properties (i) and (ii) imply the existence of a scalar field ρ, defined on B, such that

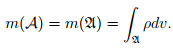                          (5.1)

ρ is called the mass density, or simply the density, of the material with which the body is made up of.
In non-relativistic mechanics mass cannot be produced or destroyed, so the mass of a body is a conserved quantity. Hence, if a body has a certain mass in the reference configuration it must stay the same during a motion. Hence, we write

m(B_r) = m(B_t) > 0,                                (5.2)

for all times t, where B_r denotes the region occupied by the body in the reference configuration and B_t denotes the region occupied by the body in the current configuration.
In the case of a material body executing a motion {B_t : t ∈ I}, the density ρ is defined as a scalar field on the configurations {B_t} and the mass content m(A_t) of an arbitrary region in the current configuration B_t is equal to the mass m(A) of A. Since, m(A) does not depend upon t we deduce directly from (5.1) the equation of mass balance

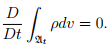                          (5.3)

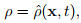 the density is assumed to be continuously differentiable jointly in the position and time variables on which it depends. Since, we are interested in the total time derivative and the current volume of the body changes with time, the differentiation and integration operations cannot be interchanged. To be able to change the order of the integration and differentiation, we have to convert it to an integral over the reference configuration. This is accomplished by using (3.75). Hence, we obtain



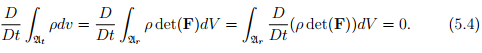
Expanding the above equation we obtain

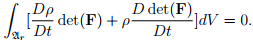                                         (5.5)

Now, we compute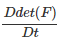 Towards this, using the chain rule for differentiation,



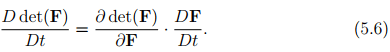
Using the result from equation (2.187),



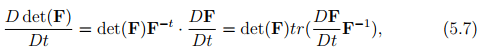
where to obtain the last expression we have made use of the definition of a dot product of two tensors, (2.71) and the property of the trace operator, (2.68). Defining, l = grad(v), it can be seen that



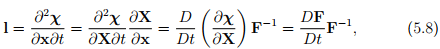
obtained using the chain rule and by interchanging the order of the spatial and temporal derivatives. Hence, equation (5.7) reduces to,

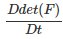 = det(F)tr(l) = det(F)tr(grad(v)) = det(F)div(v),                             (5.9)

on using the definition of the divergence, (2.208). Substituting (5.9) in (5.5) we obtain 



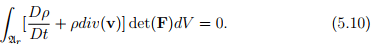
Again using (3.75) we obtain


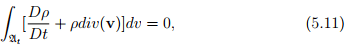
wherein the integrand is continuous in Bt and the range of integration is an arbitrary subregion of B_t . Since, the integral vanishes in B_t and in any arbitrary subregion of B_t , the integrand should vanish, i.e.,

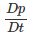 + ρdiv(v) = 0.                                                                                    (5.12) 

Subject to the presumed smoothness of ρ, equations (5.3) and (5.12) are equivalent expressions of the conservation of mass.

Further, since (5.4) has to hold for any arbitrary subpart of A_r, we get

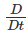 (ρ det(F)) = 0,             hence,         ρ det(F) = ρr,                          (5.13)

where ρr is the density in the reference configuration, Br. Note that, whenever the body occupies B_r, det(F) = 1 and hence, ρ = ρr, giving ρr as the constant value of ρ det(F) and hence the referential equation of conservation of mass

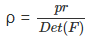                                          (5.14)

A body which is able to undergo only isochoric motions is said to be composed of incompressible material. Since, det(F) = 1 for isochoric motions, we see from equation (5.14) that the density does not change with time, t. Consequently, for a body made up of an incompressible material, if the density is uniform in some configuration it has to be the same uniform value in every configuration which the body can occupy. On the other hand if a body is made up of compressible material this is not so, in general.

Let φ be a scalar field and u a vector field representing properties of a moving material body, B, and let At be an arbitrary material region in the current configuration of B. Then show that:


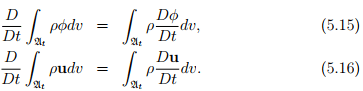
Using similar arguments as above
 

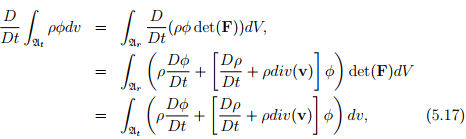
and on using equation (5.12) we obtain the first of the required results. Following the same steps as outlined above, we can show equation (5.16) is true.