TITA Based Questions: Functions | Quantitative Aptitude (Quant) - CAT PDF Download

As TITA (Type In The Answer) questions gain more weight in the CAT exam, this document focuses on Functions problems to help you prepare thoroughly and secure valuable marks.
Q1: Consider two sets A={2, 3, 5, 7, 11, 13} and B = {1, 8, 27}. Let f be a function from A to B such that for every element in B, there is at least one element a in A such that f(a) = b. Then, the total number of such functions f is
 View Answer
View Answer 
Ans: 540
Set A={2,3,5,7,11,13} so |A|=6
Set B={1, 8, 27} so |B|=3
Without any restrictions, each element in A can map to any of the 3 elements in B. Thus, the total number of functions is:
Excluding Functions That Miss One Element in B:
If a function does not map to an element in B, there are 2 elements in B left for mapping.
The total number of such functions (for each specific element not mapped) is:
Since there are 3 elements in B, the total number of such functions is:3 x 64 = 192
Adding Back Functions That Miss Two Elements in B: If a function misses two elements in B, there is only 1 element left for mapping.
The total number of such functions is: 16 = 1.
Since there are 3C2 ways to choose which two elements are missed, the total number of such functions is: 3
Using the inclusion-exclusion principle, the number of functions where all elements of B are mapped by at least one element of A is:
729 - 192 + 3 = 540.
Q2: A function f maps the set of natural numbers to whole numbers, such that f(xy) = f(x)f(y) + f(x) + f(y) for all x, y and f(p) = 1 for every prime number p. Then, the value of f(160000) is
 View Answer
View Answer 
Ans: 4095
Looking at the additional information about the prime numbers should make one realise that they are the key to solving the question.
f(16000) can be written as f(28 × 54)
Now, we can try to find these individual values:
For any prime p: f(p)=1
f(p2) = f(p)f(p)+f(p)+f(p) = 1 + 1 + 1 = 3
f(p3)=f(p2)f(p)+f(p2)+f(p) = 3 + 3 + 1 = 7
This way, we can find the function output for any prime number raised to a power.
We can see that each new exponent is twice the previous output +1, solving this way till prime raised to power 8
f(p4) = 7 + 7 + 1 = 15
f(p5) = 15 + 15 + 1 = 31
f(p6) = 31 + 31 + 1 = 63
f(p7) = 63 + 63 + 1 = 127
f(p8) = 127 + 127 + 1 = 255
Using these values in the original expression of f(28 × 54) = f(28)f(54)+f(28)+f(54) we get
f(28 × 54) = (255 × 15) + 255 + 15 = 4095
Q3: The area of the quadrilateral bounded by the Y-axis, the line x = 5, and the lines ∣x − y∣ − ∣x − 5∣ = 2, is
 View Answer
View Answer 
Ans: 45
From the inequality and nature of x, and y, we get the given diagram:
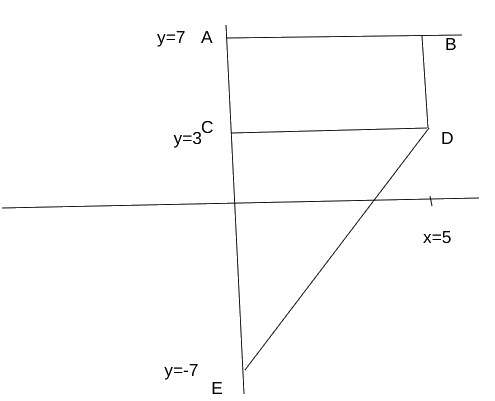
We need to find the area of the quadrilateral ABDE = area of rectangle ABCD + area of triangle CDE
⇒ Area of ABCD = (7-3)*5 = 20 units, and the area of triangle CDE = (1/2)*10*5 = 25 units.
Hence, the area of the quadrilateral ABDE = (20+25) = 45 units.
Q4: Suppose f(x, y) is a real-valued function such that f(3x + 2y, 2x - 5y) = 19x, for all real numbers x and y. The value of x for which f(x, 2x) = 27, is
 View Answer
View Answer 
Ans: 3
Given that f(3x + 2y, 2x - 5y) = 19x.
Let us assume the function f(a,b) is a linear combination of a and b.
⇒ f(3x+2y, 2x-5y) = m(3x+2y) + n(2x-5y) = 19x
⇒ 3m + 2n = 19 and 2m - 5n = 0
Solving we get m = 5 and n = 2
⇒ f(a,b) = 5a+2b
⇒ f(x,2x) = 5x + 2(2x) = 9x = 27
=> x = 3.
Q5: Let 0 ≤ a ≤ x ≤ 100 and f(x) = ∣x − a∣ + ∣x − 100∣ +∣x − a − 50∣. Then the maximum value of f(x) becomes 100 when a is equal to
 View Answer
View Answer 
Ans: 50
x > = a, so |x - a| = x - a
x < 100, so |x - 100| = 100-x
f(x) = (x-a) + (100-x) + |x-a-50| =100
or, |x-a-50| = a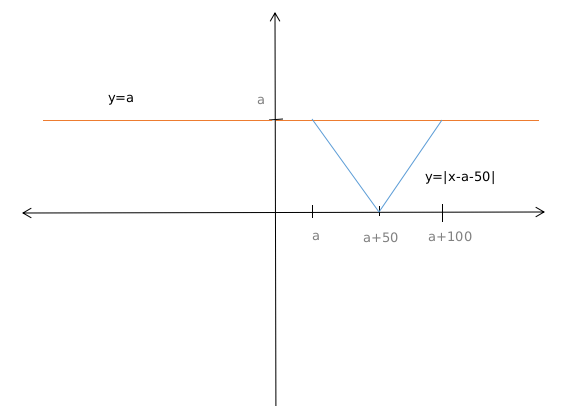 From the graph we can can see that when x = a then
From the graph we can can see that when x = a then
|x - a - 50| = a
or, a = 50
Similarly when x = a + 100
|x - a - 50| = a
or, a = 50
So value of a is 50 when f(x) is 100.
Q6: Let f(x) be a quadratic polynomial in x such that f(x) ≥ 0 for all real numbers x. If f(2) = 0 and f( 4) = 6, then f(-2) is equal to
 View Answer
View Answer 
Ans: 24
f(x) ≥ 0 for all real numbers x, so D <=0
Since f(2)=0 therefore x = 2 is a root of f(x)
Since the discriminant of f(x) is less than equal to 0 and 2 is a root so we can conclude that D = 0
Therefore f(x) = a(x − 2)2
f(4)=6
or, a(x − 2)2
a = 3/2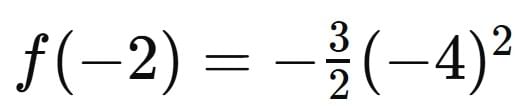 = 24
= 24
Q7: Suppose for all integers x, there are two functions f and g such that f(x)+f(x−1)−1 = 0 and g(x) = x2 . If f(x2 −x)=5, then the value of the sum f(g(5)) + g(f(5)) is
 View Answer
View Answer 
Ans: 12
f(x)+f(x−1)=1 ...... (1)
f(x2 − x) = 5 ...... (2)
g(x) = x2
Substituting x = 1 in (1) and (2), we get
f(0) = 5
f(1) + f(0) = 1
f(1) = 1 - 5 = -4
f(2) + f(1) = 1
f(2) = 1 + 4 = 5
f(n) = 5 if n is even and f(n) = -4 if n is odd
f(g(5)) + g(f(5)) = f(25) + g(-4) = -4 + 16 = 12
Q8: Let f(x) = x2 + ax + b and g(x) = f(x + 1) − f(x − 1). If f(x) ≥ 0 for all real x, and g (20) = 72. then the smallest possible value of b is
 View Answer
View Answer 
Ans: 4
f(x)= x2 +ax+b
f(x+1) = x2 +2x+1+ax+a+b
f(x−1) = x2 −2x+1+ax−a+b
g(x)=f(x+1)−f(x−1)=4x+2a
Now g(20)=72 from this we get a=−4 ; f(x) = x2 −4x +b
For this expression to be greater than zero it has to be a perfect square which is possible for b≥ 4
Hence the smallest value of 'b' is 4.
Q9: The area of the region satisfying the inequalities ∣x∣ − y ≤ 1, y ≥ 0 and y ≤ 1 is
 View Answer
View Answer 
Ans: 3 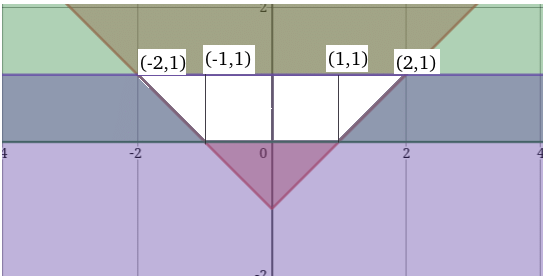 The area of the region contained by the lines ∣x∣ − y ≤ 1, y ≥ 0 and y ≤ 1 is the white region.
The area of the region contained by the lines ∣x∣ − y ≤ 1, y ≥ 0 and y ≤ 1 is the white region.
Total area = Area of rectangle + 2 x Area of triangle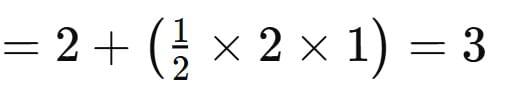
Hence, 3 is the correct answer.
Q10: In a group of 10 students, the mean of the lowest 9 scores is 42 while the mean of the highest 9 scores is 47. For the entire group of 10 students, the maximum possible mean exceeds the minimum possible mean by
 View Answer
View Answer 
Ans: 4
Let x(1) be the least number and x(10) be the largest number. Now from the condition given in the question , we can say that
x(2)+x(3)+x(4)+........x(10)= 47*9=423...................(1)
Similarly x(1)+x(2)+x(3)+x(4)................+x(9)= 42*9=378...............(2)
Subtracting both the equations we get x(10)-x(1)=45
Now, the sum of the 10 observations from equation (1) is 423+x(1)
Now the minimum value of x(10) will be 47 and the minimum value of x(1) will be 2 . Hence minimum average 425/10=42.5
Maximum value of x(1) is 42. Hence maximum average will be 465/10=46.5
Hence difference in average will be 46.5-42.5 = 4 which is the correct answer
|
184 videos|212 docs|103 tests
|
FAQs on TITA Based Questions: Functions - Quantitative Aptitude (Quant) - CAT
| 1. What are the key functions of a programming language? |  |
| 2. How do functions improve code organization in programming? |  |
| 3. What are the differences between built-in functions and user-defined functions? |  |
| 4. Can you explain the concept of function parameters and return values? |  |
| 5. Why is it important to understand scope in relation to functions? |  |
















