Tangent and Normal | Mathematics (Maths) for JEE Main & Advanced PDF Download
| Table of contents |

|
| Definition |

|
| Tangents at the Origin |

|
| Angle of intersection |

|
| Length of Tangent |

|
| Solving Equations |

|
| Shortest distance |

|
| Rate Measurement |

|
Definition
- The tangent line to the graph of f at the point P(a, f(a)) is
1. The line on P with slope f'(a) if f'(a) exists ;
2. The line x = a if= ∞.
- In neither (1) nor (2) holds, then the graph of does not have a tangent line at the point P(a, f(a)).
- In case f'(a) exists, then y - f(a) = f'(a) (x - a) is an equation of the tangent line to the graph of f at the point P(a, f(a)).
- The normal line N to the graph of a function f at the point P(a, f(a)) is defined to be the line through P perpendicular to the tangent line.
- It follows that if f'(a)
0 the slope of N is -1/f'(a) and
is an equation of N.
- If f'(a) = 0, then N is the vertical line x = a; and if the tangent line is vertical, then N is the horizontal line y = f(a).
Note :
1. The point P (x1 , y1) will satisfy the equation of the curve & the equation of tangent & normal line.
2. If the tangent at any point P on the curve is parallel to the axis of x then dy/dx = 0 at the point P.
3. If the tangent at any point on the curve is parallel to the axis of y, then dy/dx = ∞ or dx/dy = 0.
4. If the tangent at any point on the curve is equally inclined to both the axes there dy/dx = ± 1.
5. For equation of tangent at (x1, y1), substitute xx1 for x2, yy1 for y2,
for x,
for y and
for xy and keep the constant as such. This method is applicable only for second degree curves, i.e., ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
6. Method to find normal at (x1, y1) of second degree conics ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 The equation of normal at (x1, y1) is
Tangents at the Origin
- If a curve passing through the origin be given by a rational integral algebraic equation, the equation of the tangent (or tangents) at the origin is obtained by equating to zero the terms of the lowest degree in the equation.
e.g., if the equation of a curve be x2 - 4y2 + x4 + 3x3y + 3x2 y2 + y4 = 0, the tangents at the origin are given by x2 - 4y2 = 0 or x + 2y and x - 2y = 0. - In the curve x2 + y2 + ax + by = 0, ax + by = 0, is the equation of the tangent at the origin; and in the curve (x2 + y2)2 = a2 (x2 - y2), x2 - y2 = 0 is the equation of a pair of tangents at the origin.
- If the equation of a curve be x2 + y2 + x3 + 3 x2 y - y3 = 0, the tangents at the origin are given by x2 - y2 = 0 i.e. x + y = 0 and x - y = 0
Angle of intersection
Angle of intersection between two curves is defined as the angle between the two tangents drawn to the two curves at their point of intersection . If the angle between two curves is 90° then they are called ORTHOGONAL curves.
Example 1. Find the equation of tangent to the ellipse 3x2+y2+x+2y = 0 which are perpendicular to the line 4x - 2y = 1.
Sol. Since, tangent is the perpendicular to the line 4x - 2y = 1,
(slope of tangent) × (slope of normal) = –1
The given equation 3x2 + y2 + x + 2y = 0 ....(iii)
Let (x1, y1) be the point of contact of the tangent and the curve
From (i) and (iii), we get
Substituting this in (ii) [since the points lies on the curve] we get,
3x12 + 36x12 + x1 + 12x1 = 0
i.e., 13x1 (3x1 + 1) = 0 ⇒ x1 = 0, –1/3
Using (iv), x1 = 0 ⇒ y1 = 0 and x1 = –1/3 ⇒ y1 = –2
Hence, the points where tangent has slope –1/2 are P(0, 0) and Q(–1/3, –2).
Equation of tangents at P, Q are y = -1/2x i.e. x+2y = 0
i.e., 3x + 6y + 13 = 0 respectively..
Example 2. Find the equation of normal to the curve x + y = xy, where it cuts x-axis.
Sol.
Given curve is x + y = xy .....(i)
at x–axis y = 0, x + 0 = x0 ⇒ x = 1
Point is A(1, 0)
Now to differentiation x + y = xy taking log of both sides
⇒ log(x + y) = y log x
⇒
slope of normal = 1
Equation of normal is,
⇒ y = x – 1
Example 3. At what points on the curve the tangents make equal angles with co-ordintae axes ?
Sol.
Given curve is ....(1)
Differentiating both sides w.r.t.x, then dy/dx = 2x2 + 2
or 2x2 + 2x – x – 1 = 0 or (2x – 1) (x + 1)
(If 2x2 +x + 1 = 0 then x is imaginary)
From (1), for x = 1/2,
Example 4. Show that the curve x = 1 - 3t2, y = t - 3t3 is symmetrical about x-axis and has no real point for x > 1. If the tangent at the point t is inclined at an angle φ to OX. Prove that 3t = tanφ + secφ. If the tangent at P(-2, 2) meets the curve again at Q, prove that the tangents at P and Q are at right angles.
Sol. Given curve is x = 1 - 3t2 ...(1)
& y = t - 3t3 ...(2)
From (1) and (2), y = tx or 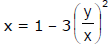 ⇒ x3 = x2 - 3y2
⇒ x3 = x2 - 3y2
Since all powers of y are even, so curve is symmetrical about x-axis.
For x > 1 ⇒ 1 – 3t2 > 1 ⇒ –3t2 > 0 Impossible
From (1) and (2),
...given (3)
Adding (3) and (4) we get, tan ø + secø = 3t
P(–2, 2)
1 – 3t2 = –2 and 2 = t – 3t3 then we get t = –1
Equation of tangent at (–2, 2) is
Therefore the tangent at t = –1 meets the curve again at
Hence the tangents at P and Q are at right angles.
Example 5. Tangent at P(2, 8) on the curve y = x3 meets the curve again at Q. Find coordinates of Q.
Sol. Equation of tangent at (2, 8) is y = 12x - 16
Solving this with y = x3 we get x3 - 12x + 16 = 0
this cubic must give all points of intersection of line and curve y = x3
i.e., point P and Q.
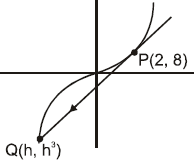
But, since line is tangent at P so x = 2 will be a repeated root of equation x3 -12x + 16 = 0 and another root will be x = h.
Using theory of equations sum of roots ⇒ 2 + 2 + h = 0 ⇒ h = -4
Hence coordinates of Q are (-4, -64)
Example 6. If the normal to the curve x2/3 + y2/3 = a2/3 makes an angle φ with the axis of x, show that its equation is y cosφ - x sinφ = a cos 2φ.
Sol. Given curve is x2/3 + y2/3 = a2/3 ...(1)
Differentiating both sides w.r.t.x, we get
From (1) and (2), y2/3 (1 + tan2Ø) = a2/3 Þ y2/3 = a2/3 cos2Ø
y = a cos3 Ø and x = a sin3 Ø
Therefore equation of normal is y – a cos3 Ø = tan Ø (x – a sin3 Ø)
y cos Ø– a cos4 Ø = x sin Ø – a sin4 Ø
y cosØ– x sin Ø = a (cos4 Ø– sin4 Ø)
= a (cos2 Ø + sin2 Ø) (cos2 Ø- sin2 Ø) = a . 1 . cos 2Ø
Hence y cos Ø– x sin Ø = a cos 2Ø
Example 7. (a) Find y' if x3 + y3 = 6xy.
(b) Find the tangent to the folium of Descartes x3 + y3 = 6xy at the point (3, 3).
(c) At what points on the curve is the tangent line horizontal ?
Sol. (a) Differentiating both sides x3 + y3 = 6xy with respect to x, regarding y as a function of x, and using the Chain Rule on the y3 term and the Product Rule on the 6xy term, we get
3x2 + 3y2y' = 6y + 6xy' or x2 + y2y' = 2y + 2xy'
We now solve for y' :y2y' – 2xy' = 2y – x2
(y2 – 2x)y' = 2y – x2,
(b) When x = y = 3
So, tangent to the folium of Descartes is y – 3 = –1(x – 3) or x + y = 6
(c) The tangent line is horizontal if y' = 0. Using the expression for y' from part (a), we see that y' = 0 when 2y – x2 = 0. Substituting y = 1/2x2 , n the equation of the curve, we get
which simplifies to x6 = 16x3. so either x = 0 or x3 = 16. If x = 161/3 = 24/3, then y = 1/2(28/3) = 25/3. Thus, the tangent is horizontal at (0, 0) and at (24/3, 25/3).
Example 8. In the curve xa yb = ka + b, (a b > 0) prove that the portion of the tangent intercepted between the coordinate axes is divided at its point of contact into segments which are in constant ratio.
Sol. Let P(x1, y1) be the point of contact of the tangent.
Here, xayb = ka + b
∴ a log x + b log y = (a + b) log k.
Solving with y = 0,
Let P divide AB in the ratio λ : 1. Then
P divides AB in the constant ratio b : a.
Example 9. Find the angle between curves y2 = 4x and y = e-x/2
Sol.
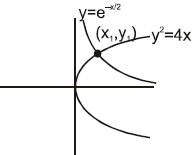
Let the curves intersect at point (x1,y1)
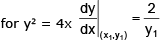
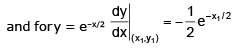
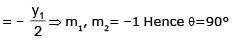
Note: here that we have not actually found the intersection point but geometrically we can see that the curves intersect.
Example 10. Show that the curves y = 2 sin2x and y = cos 2x intersect at π/6. What is their angle of intersection ?
Sol. Given curves are y = 2 sin2 x ...(1)
and y = cos 2x ...(2)
Solving (1) and (2), we get 2 sin2 x = cos 2x
⇒ 1 – cos 2x = cos 2x ⇒ cos2x = 1/2 ⇒ cos π/3 ⇒ 2x = ± π/3
x = ±π/6 are the points of intersection
From (1), dy/dx = 4 sin x cos x = 2 sin 2x = m1 (say)
From (2) dy/dx = -2 sin 2x = m2 (say)
If angle of intersection is θ, then tanθ 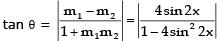
∴ 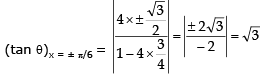
∴ 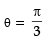
Example 11. Show that the angle between the tangents at any point P and the line joining P to the origin `O' is the same at all points of the curve ln (x2 + y2) = c tan-1 (y/x) where c is constant.
Sol. Let the point P(x, y) on the curve ln (x2 + y2) = c tan-1 (y/x) where c is constant.
Differentiating both sides w.r.t. x, we get
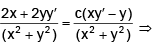
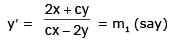
Slope of OP = y/x = m2 (say)
Let the angle between the tangents at P and OP be θ
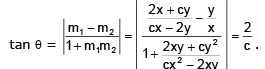
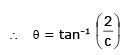 which is independent of x and y.
which is independent of x and y.
Example 12. Show tht the curves 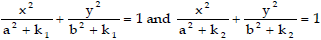 intersect orthogonally.
intersect orthogonally.
Sol.
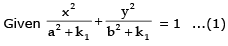
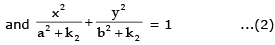
Subtracting (2) from (1), we get 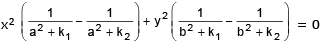
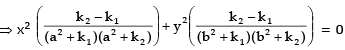
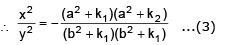

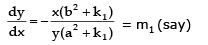
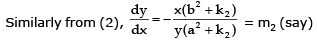
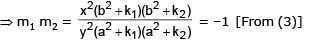
Hence given curves intersect orthogonally.
Example 13. Prove that the curves xy = 4 and x2 + y2 = 8 touch each other.
Sol.
Equation of the given curves are xy = 4 ....(i) and x2 + y2 = 8 ....(ii)
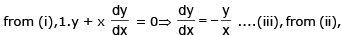
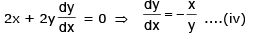
Putting the value fo y from (i) i (ii), we get x2 + 16/x2 = 8 or or x4 + 16 = 8x2
or x4 – 8x2 + 16 = 0 or (x2 – 4)2 = 0 or x2 – 4 = 0 or x2 = 4
from (i) ; when x = 2, y = 2 and when x = –2, y = -2
Hence points of intersection of the two curves are (2, 2) and (–2, –2).
Slope of the tangent to the curve (i) at point (2, 2) ⇒ m1 = -2/2 = -1 ...(from iii)
Slope of tangent to the curve (ii) at point (2, 2) ⇒ m2 = -2/2 = -1....( from iv)
Since m3 = m4, hence the two curves touch each other at (-2, -2). Thus curves (i) and (ii) touch each other.
Slope of tangent to curve (i), 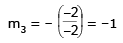
Slope of tangent to curve (ii), 
Since m3 = m4, hence the two curves touch each other at (–2, –2). Thus curves (i) and (ii) touch each other.
Example 14. The gradient of the common tangent to the two curves y = x2 - 5x + 6 & y = x2 + x + 1 is
(A) - 1/3
(B) - 2/3
(C) - 1
(D) - 3
Sol. y = ax + b on solving with both curves and putting D = 0 gives
a2 + 10a + 4b + 1 = 0 and a2 - 2a + 4b - 3 = 0 ⇒ a = - 1/3 & b = 5/9
⇒ 3x + 9y = 5 ; point of contact (7/3, - 2/9) & (- 2/3, 7/9)
Length of Tangent
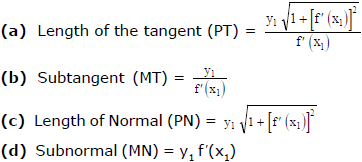
Example 15. What should be the value of n in the equation of curve y = a1 - n. xn, so that the sub-normal may be of constant length ?
Sol. Given curve is y = a1 - n . xn
Taking logarithm of both sides, we get, ln y = (1 - n) ln a + n ln x
Differentiating both sides w.r.tx, we get 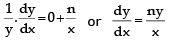 ...(1)
...(1)
Lengths of sub-normal = y dy/dx = y .ny/x ....{from 1}
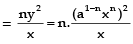
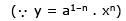
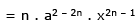
Since lengths of sub-normal is to be constant, so x should not appear in its value i.e., 2n – 1 = 0. n =1/2
Example 16. If the relation between sub-normal SN and sub-tangent ST at any point S on the curve
by2 = (x + a)3 is p(SN) = q(ST)2; then p/q is
(A) 8b/27
(B) b
(C) 1
(D) none of these
Sol.
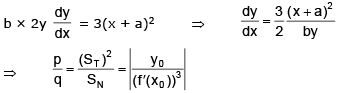
Let a point by (x0, y0) lying on the curve by = (x0 + a)3 ....(i)
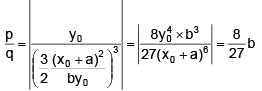 (from equation (i))
(from equation (i))
Example 17. For the curve y = 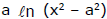 show that sum of lengths of tangent & subtangent at any point is proportional to coordinates of point of tangency.
show that sum of lengths of tangent & subtangent at any point is proportional to coordinates of point of tangency.
Sol.
Let point of tangency be (x1, y1) ⇒ 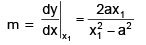
tangent + subtangent = 
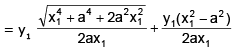
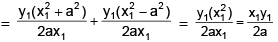 Hence proved.
Hence proved.
Example 18. Show that the segment of the tangent to the curve y = 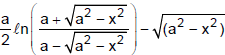 contained between the y-axis and point of tangency has a constant length.
contained between the y-axis and point of tangency has a constant length.
Sol.
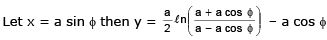
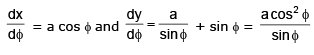
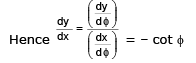
Equation of tangent at ‘ø’ y – a ln cot ø/2 + a cos ø = 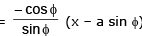
⇒y sin ø – a sinø ln cot ø/2 + a sin ø cos ø - x cosø + a sin ø cos ø
⇒x cos ø+ y sin ø = a sin ø ln cot ø/2
Point on y-axis P ≡ (0, a ln cot ø/2) and point of tangency
Q≡ (a sinø a ln cotø/2 – a cos ø)
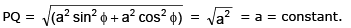
Solving Equations
Example 19. For what values of c does the equation ln x = cx2 have exactly one solution ?
Sol.
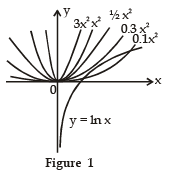
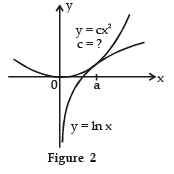
Let's start by graphing y = In x and y = cx2 for various values of c. We know that for c * 0, y = cx2 is a parabola that opens upward if c > 0 and downward if c < 0. Figure 1 shows the parabolas y = cx2 for several positive values of c. Most of them don't intersect y = In x at all and one intersect twice. We have the feeling that there must be a value of c (somewhere between 0.1 and 0.3) for which the curves intersect exactly once, as in Figure 2.
To find that particular value of c, we let 'a' be the x-coordinate of the single point of intersection. In other words, In a = ca2, so 'a' is the unique solution of the given equation. We see from Figure 2 that the curves just touch, so they have a common tangent line when x = a. That means the curves y = In x and y=cx2 have the same slope when x = a. Therefore 1/a = 2ca
Solving the equation In a = ca2 and 1/a = 2ca
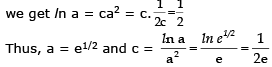
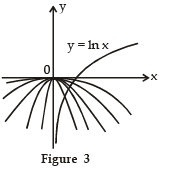
For negative values of c we have the situation illustrated in Figure 3: All parabolas y = cx2 with negative values of c intersect y = In x exactly once. And let's not forget about c = 0: The curve y = 0 x2 = 0 just he x-axis, which intersects y = In x exactly once.
To summarize, the required values of c are c=1/(2e) and c<0
Example 20. The set of values of p for which the equation px2 = ln x possess a single root is
Sol.
for p ≤ 0, there is obvious one solution ; for p > 0 one root
⇒ the curves touch each .
2 px1 = 1/x1 ⇒ x12 = 1/2p ;
Also px12 = ln x1 ⇒ p (1/2p) = ln x1 ⇒ x1 = e1/2
⇒ 2 p = 1/e ⇒ p = 1/2e . Hence p ∈ (- ∝, 0] U {1/2e}
Shortest distance
Shortest distance between two non-intersecting curves always along the common normal (wherever defined)
Example 21. Find the shortest distance between the line y = x - 2 and the parabola y = x2 + 3x + 2.
Sol. Let P(x1, y1) be a point closest to the line y = x - 2 then 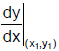 = slope of line
= slope of line
⇒ 2x1 + 3 = 1 ⇒ x1 = - 1 ⇒ y1 = 0 Hence point (-1, 0) is the closest and its perpendicular distance from the
line y = x - 2 will give the shortest distance ⇒ p = 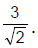
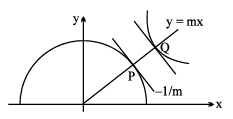
Example 22. Let P be a point on the curve C1: y = 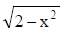 and Q be a point on the curve C2: xy = 9, both P and Q lie in the first quadrant. If 'd' denotes the minimum value between P and Q, find the value of d2.
and Q be a point on the curve C2: xy = 9, both P and Q lie in the first quadrant. If 'd' denotes the minimum value between P and Q, find the value of d2.
Sol. Note that C1 is a semicircle and C2 is a rectangular hyperbola.
PQ will be minimum if the normal at P on the semicircle is also a normal at Q on xy = 9
Let the normal at P be y = mx ....(1) (m > 0) solving it with xy = 9
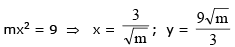
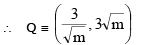
differentiating xy = 9
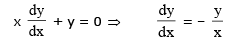
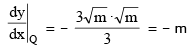
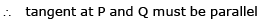
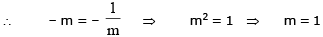
∴ normal at P and Q is y = x
solving P(1, 1) and Q(3, 3)
(PQ)2 = d2 = 4 + 4 = 8
Rate Measurement
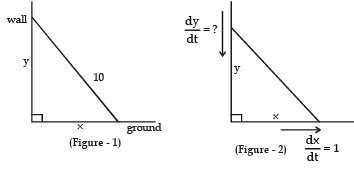
Example 23. A ladder 10 ft long rests against a vertical wall. If the bottom of the ladder slides away from the wall at a rate of 1 ft/s, how fast is the top of the ladder sliding down the wall when the bottom of the ladder is 6 ft from the wall ?
Sol. We first draw a diagram and label it as in Figure 1. Let x feet be the distance from the bottom of the ladder to the wall and y feet the distance from the top of the ladder to the ground. Note that x and y are both function of t (time). We are given that dx/dt = 1 ft/s and we are asked to find dy/dt when x = 6 ft (see Figure 2). In this problem, the relationship between x and y is given by the Pythagorean Theorem : x2 + y2 = 100
Differentiating each side with respect to t using the Chain Rule, we have 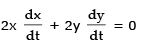
and solving this equation for the desired rate, we obtain 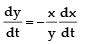
When x = 6, the Pythagorean Theorem gives y = 8 and so, substituting these values and dx/dt = 1,
we have 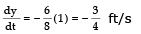
The fact that dy/dt is negative means thatthe distance from the top of the ladder to the ground is decreasing at a rate of 3/4 ft/s In other words, the top of the ladder is sliding down the wall at a rate of 3/4 ft/s .
Example 24. A water tank has the shape of an inverted circular cone with base radius 2 m and height 4 m. If water is being pumped into the tank at a rate of 2 m3/min, find the rate at which the water level is rising when the water is 3 m deep.
Sol.
We first sketch the cone and label it as in Figure. Let V, r, and h be the volume of the water, the radius of the surface, and the height at time t, where t is measured in minutes.
We are given that dV/dt = 2m3/min and we are asked to find dh/dt when h is 3 m. The quantities V and h are related by the equation V = 1/3pr2hBut it is the very useful to express V as a function of h alone.
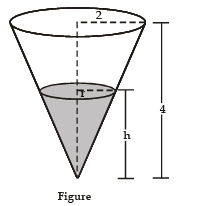
In order to eliminate r, we use the similar triangles in Figure to write 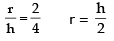 and the expression for V becomes
and the expression for V becomes 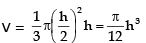
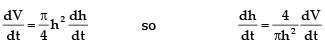
Substituting h = 3 m and dV/dt = 2m3/min, we have 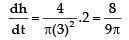
The water level is rising at a rate of 8/(9p) ≈ 0.28 m/min.
Example 25. A man walks along a straight path at the speed of 4 ft/s. A searchlight is located on the ground 20 ft from the path and is kept focused on the man. At what rate is the searchlight rotating when the man is 15 ft from the point on the path closest to the searchlight ?
Sol. We draw Figure and let x be the distance from the man to the point on the path closest to the searchlight. We let θ be the distance from the man to the point on the path closest to the searchlight and the perpendicular to the path.
We are given that dx/dt = 4 ft/s and are asked to find dq/dt when x = 15. The equation that relates
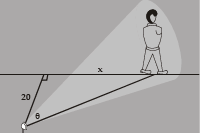
Differentiating each side with respect to t, we get dx/dt = 20sec2 θ dθ/dt
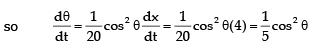
when x = 15, the length of the beam is 25, so cosθ = 4/5
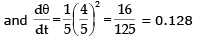
The searchlight is rotating at a rate of 0.128 rad/s.
Example 26. Two men A and B start with velocities v at the same time from the junction of two roads inclined at 45º to each other. If they travel by different roads, find the rate at which they are being separated.
Sol.
Let L and M be the positions of men A and B at any time t,
Let OL = x and LM = y. Then OM = x
given, dx/dt = v; to find dy/dt from ΔLOM,
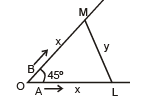
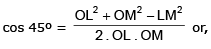
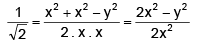
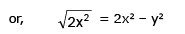
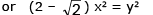
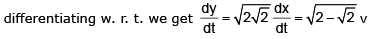
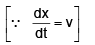
∴ they are being separated from each other at the rate 
Example 27. A variable triangle ABC in the xy plane has its orthocentre at vertex 'B', a fixed vertex 'A' at the origin & the third vertex 'C' restricted to lie on the parabola y = 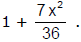 The point B starts at the point (0, 1) at time t = 0 & moves upward along the y axis at a constant velocity of 2 cm/sec. How fast is the area of the triangle increasing when t = 7/2 sec ?
The point B starts at the point (0, 1) at time t = 0 & moves upward along the y axis at a constant velocity of 2 cm/sec. How fast is the area of the triangle increasing when t = 7/2 sec ?
Sol.
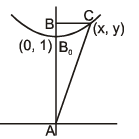
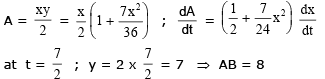
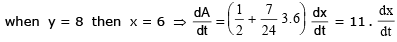

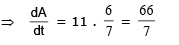
Example 28. Find the approximate value of (1.999)6.
Sol.
Let f(x) = x6. Now, f(x + δx) – f(x) = f'(x) . δx = 6x5 δx
We may write, 1.999 = 2 – 0.001
Taking x = 2 and δx = –0.001, we have f(1.999) – f(2) = 6(2)5 × – 0.001
⇒ f(1.999) = f(2) – 6 × 32 × 0.001 = 64 – 64 × 0.003 = 6
|
172 videos|503 docs|154 tests
|
FAQs on Tangent and Normal - Mathematics (Maths) for JEE Main & Advanced
| 1. What are tangents at the origin? |  |
| 2. What is the angle of intersection between two tangents at the origin? |  |
| 3. How do you find the length of a tangent to a curve at a given point? |  |
| 4. How do you solve equations involving tangents and normals? |  |
| 5. What is the shortest distance from a point to a curve? |  |





















