The Gas Laws | Chemistry for JEE Main & Advanced PDF Download
| Table of contents |

|
| Boyle's Law |

|
| Charles' Law |

|
| Pressure-Temperature Law (Gay Lussac's Law) |

|
| Avogadro's Law |

|
Boyle's Law
It relates the volume and the pressure of a given mass of a gas at constant temperature.
Boyle's law states that, at constant temperature, the volume of a sample of a gas varies inversely with the pressure.
∴ P ∝ 1/V (when temperature and number of moles are kept constant)
The proportionality can be changed into equality by introducing a constant k, i.e.,
Boyle's law can be verified by any one of the following three ways graphically.
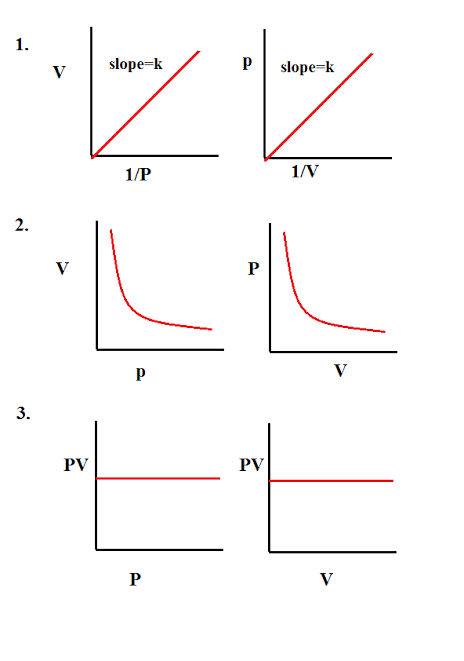
Alternatively, Boyle's law can also be stated as follows :
"Temperature remaining constant , the product of pressure and volume of a given mass of a gas is constant".
The value of the constant depends upon the amount of a gas and the temperature.
Mathematically, it can be written as,
P1V1 = P2V2 = P3V3 = ..............
Location of straight line and curve changes with temperature in the isotherm shown in the following figure.
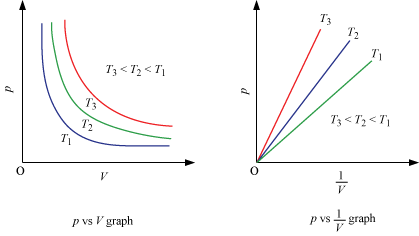
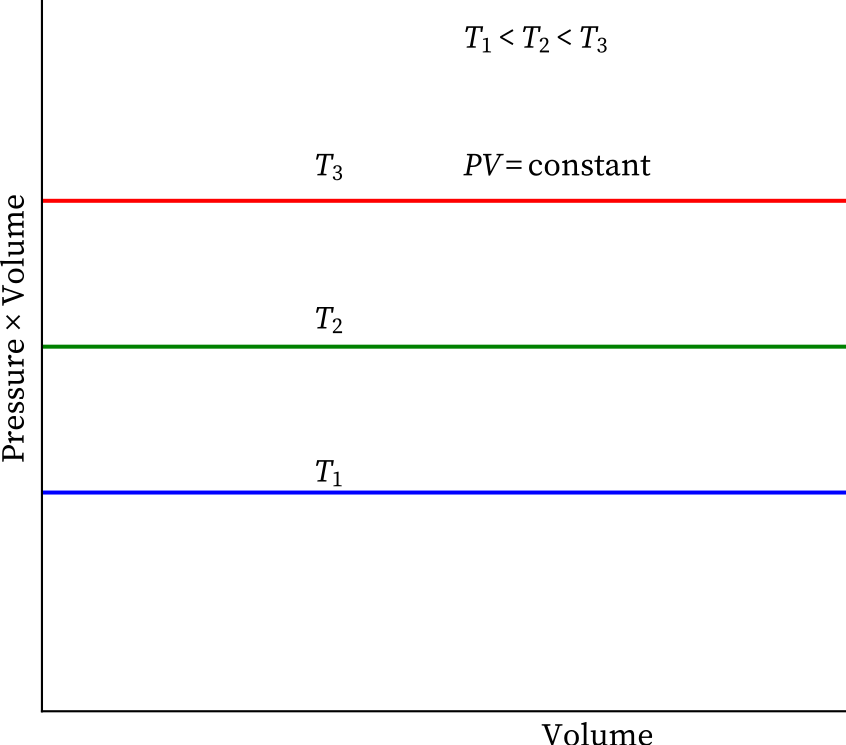
According to Boyle's law, PV = Constant at constant temperature
∴ log P log V = constant
log P = -log V = constant
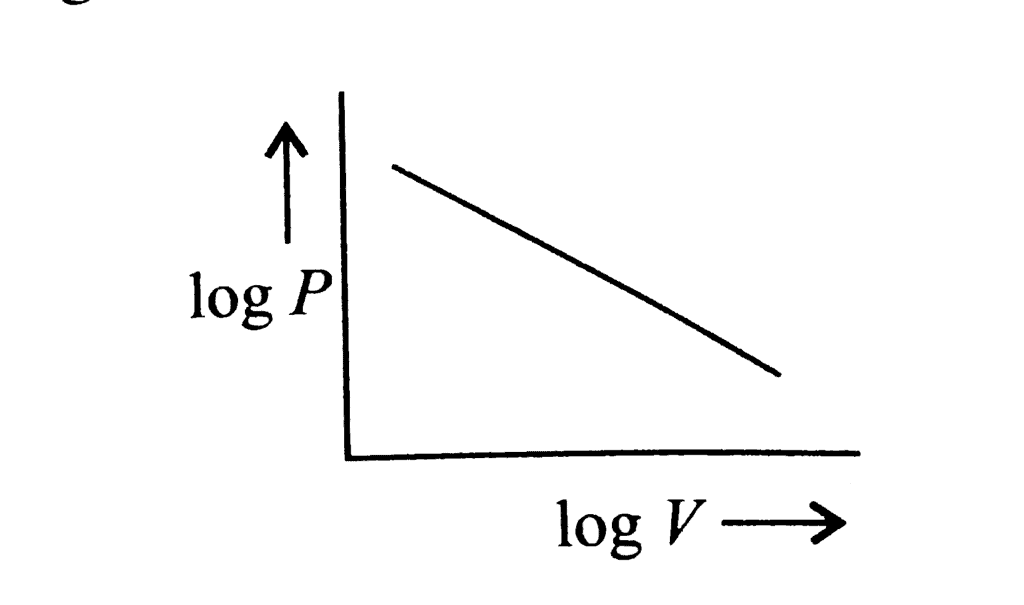
Illustration 1: A gas is present at a pressure of 2 atm. What should be the increase in pressure so that the volume of the gas can be decreased to 1/4th of the initial value if the temperature is maintained constant.
Solution: PV = constant for a given mass of gas at constant pressure
⇒P1V1 = P2 V2
P1 = 2atm
V2 = V/4
P2 =?
Now, ⇒ P2 = 8 atm
∴ Pressure should be increased from 2 to 8 atm
∴ total increase = 8 - 2 = 6 atm.
Illustration 2: A sample of gas occupies 10 litre under a pressure of 1 atmosphere. What will be its volume if the pressure is increased to 2 atmospheres? Assume that the temperature of the gas sample does not change.
Solution: Mass and temperature is constant hence we can use Boyle's law
P1V1 = P2V2
Given P1 = 1 atm, V1 = 10 litre, P2 = 2 atm, V2 = ?
1 × 10 = 2 × V2 ⇒ V2 = 5 litre
Charles' Law
It relates the volume and temperature of a given mass of a gas at constant pressure.
For each degree change of temperature, the volume of a sample of a gas changes by the fraction of its volume at 0 °C.
Let the volume of a given amount of gas be V0 at 0°C. The temperature is increased by t°C and the new volume becomes Vt
Thus, or
A new temperature scale was introduced known as Kelvin scale or absolute scale (named after the British physicist and mathematician Lord Kelvin). The lower limit of the scale is called absolute zero which corresponds to - 273°C.
At absolute zero or - 273 °C, all molecular motions would stop and the volume of the gas would become zero. The gas would become a liquid or solid. Thus, absolute zero is that temperature at which no substance exists in the gaseous state. The temperature in absolute scale is always obtained by adding 273 to the temperature expressed in °C.
K = (t°C 273)
This new temperature scale may be used for deducing Charles' law.
By substituting T for 273 t and T0 for 273 in Eq. (i).
or
or V/T = constant, if pressure is kept constant

(This graph is called isobar)
Alternatively, Charles' law can be stated as follows:
"The volume of a given amount of a gas at constant pressure varies directly as its absolute temperature".
V ∝ T (if pressure is kept constant)
Illustration 3: 1 mole of an ideal gas at constant atmospheric pressure is heated to increase its volume by 50% of initial volume. The change in temperature made was 300 K to T K. Then calculate final temperature.
Solution: At constant pressure for a given amount of gas
⇒
(V1 = V, T1= 300 K, V2 = 1.5V)
T = 450 K
Pressure-Temperature Law (Gay Lussac's Law)
It relates the pressure and absolute temperature of a given mass of a gas at constant volume.
Volumes remaining constant, the pressure of a given mass of a gas increases or decreases by of its pressure at 0°C per degree change of temperature.
Pt = P0 or Pt = P0
or Pt = P0
= P0
or or (if volume and number of moles are kept constant)
At constant volume, the pressure of a given amount of a gas is directly proportional to its absolute temperature.
Illustration 4: Pressure of gas contained in a closed vessel is increased by 0.4%, when heated by 1ºC. Calculate its final temperature. Assume ideal nature.
Solution: Since no information is given about volume hence we can assume that volume is constant and use =
given P1 = P, T1 = T, P2 = P = 1.004 P, T2 = T 1
=
⇒ T = 250 K
Avogadro's Law
For Solid, Liquid and Gas
1 mole of any substance contains Avogadro's number (NA) of molecules/atoms/particles etc.
NA = 6.023 × 1023
For Gases
In 1812, Amadeo Avogadro stated that samples of different gases which contain the same number of molecules (any complexity, size, shape) occupy the same volume at the same temperature and pressure. It follows from Avogadro's hypothesis that V ∝ n (T and P are constant).
V ∝ n (T, P constant) ⇒
STP: 273.15 K 1 atm
SATP: 298.15 K 1 bar
|
334 videos|660 docs|300 tests
|
FAQs on The Gas Laws - Chemistry for JEE Main & Advanced
| 1. What is Boyle's Law? |  |
| 2. What is Charles' Law? |  |
| 3. What is the Pressure-Temperature Law (Gay Lussac's Law)? |  |
| 4. What is Avogadro's Law? |  |
| 5. What are the Gas Laws? |  |





















