The Gaseous State | General Awareness - Bank Exams PDF Download
Introduction
A substance can exist in three phases—solid, liquid, or gas—depending on the balance between Mutual Attraction (MA) and Escaping Tendency (ET):
Solid State: When MA is greater than ET, the substance is in a solid state, with tightly packed molecules.
Liquid State: If MA is slightly greater than ET, the substance is a liquid, allowing molecules to move past each other.
Gaseous State: When MA is much less than ET, the substance is a gas, with widely spaced molecules that move freely.

The gaseous state is the simplest, characterized by:
Volume Sensitivity: Gases respond significantly to changes in pressure and temperature.
Large Molecular Distances: Molecules are far apart compared to their size.
Weak Van der Waals Forces: These allow gas molecules to move independently at speeds of about 400 m/s.
Gases behave uniformly under similar conditions of temperature and pressure, regardless of their nature. This simplicity makes gases distinct from solids and liquids.
Measurable properties of gases
Mass
The gases do possess mass. The mass of gas is generally used in the form of the number of moles which is related as:
No. of moles =
- Two other useful formula to calculate number of moles of gas are:
(i) No. of moles =
(ii) No. of moles = - When a container contains more than one gas then the molecular mass of the mixture is termed as effective molecular mass (EMM) which is intermediate between molecular masses of all the gases present in the container i.e.
Effective molecular mass =
[Question: 891969
Volume
Volume of gas is nothing but volume of the container in which it is present.

- Relation between different units of volume:
1 m3 = 103 dm3 = 103 litre =106 cm3 = 106 ml = 109 mm
Temperature
Degree of hotness or coldness of a body is measured by temperature.
=
=
C - Celsius scale, K - Kelvin scale, F - Fahrenheit scale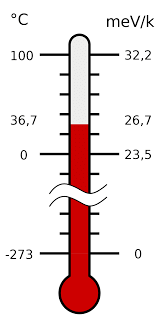 Thermometer calculating temperature
Thermometer calculating temperature
Note: In all the problems of gaseous state (i.e. in all gas law equations), the temperature must be expressed in the kelvin scale. i.e. , t °C + 273 = T K
Pressure
Force acting per unit area. Pressure is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Pressure is force applied to object
P = 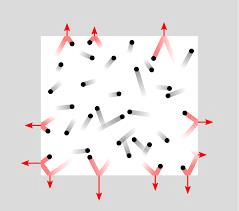
Units:
CGS: dyne/cm2
SI: Newton/m2 (1N/m2 = 1Pa)
Relation between CGS and SI units: 1 N/m2 = 10 dyne/cm2
Relation between different units of pressure:
1 atm = 76 cm of Hg = 760 mm of Hg = 760 torr = 1.01325×105 N/m2 = 101.325 kPa = 1.01325 bar = 14.7 lb/In2 (Psi) = 10.33 meters of H2O
Density
Density is a characteristic property of a substance. It is defined as mass per unit volume.
d = m/v
Units:
CGS: g/cm3
SI: kg/m3
Relation between CGS and SI units: 1 kg/m3 = 10-3 g/cm3
Density of gases
1. Absolute density: Mass per unit volume i.e. d = m/v. Its unit is gram per litre.
It is a function of temp., pressure, no. of moles.
2. Relative density: It is defined as the ratio of the density of a substance to the density of a standard, usually water for a liquid or solid, and air for gas.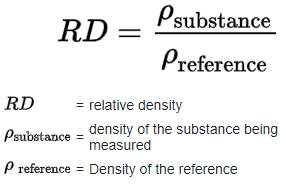 Relative to hydrogen turned as vapour density i.e. VD =
Relative to hydrogen turned as vapour density i.e. VD =
Since it is a ratio, therefore, it has no unit and independent of Pressure, Temperature.
Note:
- Mass, volume and no. of moles are extensive properties that depend on mass hence then all directly additive in nature.
- Density, pressure, and temperature are intensive properties they do not depend on mass hence they are non-additive in nature.
Ideal Gas Equation
- Combining all these gas laws, a simple equation can be derived that relates P, V, n, and T for a gas, PV = nRT (for n moles of gas)
⇒ Combined gas law:=
- P is the pressure of the gas and can be expressed in atm or Pa.
The volume must be expressed in liters or m3 respectively.
n is the number of moles
T is the temperature in Kelvin.
R is called the universal gas constant. - Numerical Values of R
(i)In litre atmosphere: 0.0821 litre atm deg-1 mole-1
(ii)In ergs: 8.314 x 107 erg deg-1 mole-1
(iii)In joules: 8.314 jouls deg-1 mol-1
(iv)In calories: 1.937 cal deg-1 mole-1
Example: An open vessel at 27°C is heated until 3/5th of the air in it has been expelled. Assuming that the volume of the vessel remains constant find
(A) the air escaped out if vessel is heated to 900K.
(B) temperature at which half of the air escapes out.
Sol. One should clearly note the fact that on heating a gas in a vessel, there are the number of moles of gas which go out, the volume of the vessel remains constant.
Let initial no. of moles of gas at 300 K be 'n'.
On heating 3/5 moles of air escape out at temperature T.
∴ Moles of air left at temperature T = n - 3n/5 = 2n/5
(A) On heating vessel to 900 K, let n1 moles be left,
⇒ n1 x 900 = 300 x n [∵ n1T1 = n2T2 ]
∴ moles escaped out = n - n/3 = 2n/3 moles
(B) Let n/2 moles escape out at temperature T, then
⇒ (n/2) x T = n x 300 [∵ n1T1 = n2T2 ]
⇒ T = 600 K
Example: 5g of ethane is confined in a bulb of one-liter capacity. The bulb is so weak that it will burst if the pressure exceeds 10 atm. At what temperature will the pressure of gas reach the bursting value?
Solution: PV = nRT ⇒ 10 ×1 = × 0.082 × T
T = = 60 × 12.18 = 730.81 K = 457.81ºC
Relation Between Molecular Mass and Gas Densities 1. Actual Density
- For an ideal gas, PV = nRT or
,
where w = mass of the gas in gms and M = Molecular wt. in gms.
∴or PM = ρRT, (where ρ is the density of the gas =
)
⇒ =
(for same gas at different temperature and pressure)
=
(for different gases at same temperature & pressure)
(Where d = density of gas)
Example: The density of an unknown gas at 98°C and 0.974 atm is 2.5 × 10-3 g/ml. What is the mol wt. of gas?
Sol. Density = 2.5 × 10-3 g/ml = 2.5 g/L
∵ PM = ρRT
⇒ 0.974 × M = 2.5 × 0.0821 × 371
⇒ M = 78.18.
2. Vapour Density
- For gases another term that is often used is vapour-density.
- Vapour density of a gas is defined as the ratio of the mass of the gas occupying a certain volume at a certain temperature and pressure to the mass of hydrogen occupying the same volume at the same temperature and pressure
i.e. Wgas =and
mol. wt. of hydrogen is 2)
(Vapour density of gas)
- Vapour density of a gas is same at any temperature, pressure, and volume.
Example: When 3.2 g of sulphur is vapourised at 450°C and 723 mm pressure, the vapours occupy a volume of 780 ml. What is the molecular formula of sulphur vapours under these conditions? Calculate the vapour density also.
Sol. PV = nRT ⇒ ×
=
× 0.082 × 723
M = 255.9
no. of atoms of sulphur in one molecule = 8
Molecular formula of sulphur = S8
V. D. = =
⇒ 127.99
Dalton's Law of Partial Pressure
- The total pressure of a mixture of non-reacting gases is equal to the sum of their partial pressures.
- By Dalton's Law, PT = P1 P2 ..............
- The partial pressure of a gas in a mixture is means, the pressure that the gas will exert if it occupies alone the total volume of the mixture at the same temperature.
- Derivation:
n = n1 n2 …⇒
⇒ P = P1 P2 …
Assumption: Volume of all the gases is same as they are kept in same container. - Relationship between partial pressure and number of moles
Important formula:
(i)where x1 = mole fraction of gas
(ii) Partial pressure of a gas in the mixture - Partial pressure and aqueous tension: Dalton's law is used to calculate the pressure of a dry gas when it is collected over water at atmospheric pressure.
By Dalton's law,
Pressure of dry gas = atmospheric pressure - aqueous tension
Aqueous tension depends on temperature. It increases with temperature and becomes 760 mm at 100°C.
Example: A gaseous mixture contains 55% N2, 20% O2, and 25% CO2 by mass at a total pressure of 760 mm. Calculate the partial pressure of each gas.
Sol. Total mass of the gases = 100 g
= 55g,
= 20 g,
= 25g
= 55/28 = 1.964,
= 20/32 = 0.625,
= 25/44 = 0.568
Total moles = 3.157
Example: A mixture containing 1.6 g of O2, 1.4g of N2 and 0.4 g of He occupies a volume of 10 litre at 27°C. Calculate the total pressure of the mixture and partial pressure of each compound.
Sol. PV = nRT
V = 10 litre, T = 27ºC = 300K
=
= 0.1,
=
= 0.05,
=
= 0.05
Total no. of moles = 0.1 + 0.05 + 0.05 = 0.2
PV = nRT ⇒ P× 10 = 0.2 × 0.082 × 300 = 0.04926 ⇒ P = 0.492 atm
Partial pressure = Total pressure × mole-fraction
PHe = 0.492 × = 0.246 atm
= 0.492 ×
= 0.123 atm
= 0.492 ×
= 0.123 atm
Graham's Law of Diffusion
- Diffusion is the tendency of any substance to spread throughout the space available to it.
- Diffusion will take place in all direction and even against gravity.
- The streaming of gas molecules through a small hole is called effusion.
- According to Graham, the rate of diffusion (or effusion) of a gas at constant pressure and temperature is inversely proportional to the square root of its molecular mass.
, at constant P and T
∴, at constant P and T
- Since molecular mass of gas = 2 × vapour density,
∴, at constant P and T
- The rate of diffusion (or effusion) r of two gases under different pressure can be given by
at constant T only.
Therefore, according to Graham's law of diffusion (effusion) at constant P and T.
(i)
where d1 and d2 are the respective densities and V1 and V2 are volumes diffused (effused) in time t1 and t2.
(ii)
where n1, n2 are moles diffused (effused) in time t1 and t2.
(iii)
where x1 and x2 are distances travelled by molecules in narrow tube in time t1 and t2.- r =
=
=
 View Answer
View Answer 
Note:
- It should be noted that the rate of diffusion or effusion actually depends on the pressure difference of the gas and not simply on its pressure. Moreover, the pressure difference is to be measured for this gas-only i.e. if a container holds [He] at a pressure of 0.1 atm and if a small pin-hole is made in the container and if the container is placed in a room, then the rate of effusion of He gas from the container to outside depends only on its pressure difference, which is 0.1-0 (as there is no He in the atmosphere). This implies that the diffusion of a gas is not dependent on the diffusion of any other gas.
- Whenever we consider the diffusion of gas under experimental conditions, we always assume that the gas diffuses in a vacuum and during the time period for which the diffusion has studied the rate of diffusion (or the composition of diffusing or an effusing mixture of gases) remains constant.
Example: Pure O2 diffuses through an aperture in 224 seconds, whereas a mixture of O2 and another gas containing 80% O2 diffuses from the same in 234 sec under the similar condition of pressure and temperature. What is the molecular wt. of gas?
Sol. The gaseous mixture contains 80% O2 and 20% gas.
∴ The average molecular weight of mixture … (i)
Now for the diffusion of the gaseous mixture and pure O2
or
… (ii)
∴
By (i) and (ii), mol weight of gas (M) = 46.6
Example: Calculate the relative rates of diffusion of 235UF6 and 238UF6 in the gaseous state (Atomic mass of F = 19).
Sol. and
(at F = 19)
=
=
= 1.0042
Deviations from Ideal Behaviour
- An ideal gas is one that obeys the gas laws of the gas equation PV = RT at all pressure and temperatures. However, no gas in nature is ideal. Almost all gases show significant deviations from the ideal behaviour.
- Thus the gases H2, N2 and CO2 which fail to obey the ideal-gas equation are termed as non-ideal or real gases.
Compressibility Factor
- The extent to which a real gas departs from the ideal behaviour may be depicted in terms of a new function called the compressibility factor, denoted by Z.
- It is defined as:
- The deviations from ideality may be shown by a plot of the compressibility factor Z, against P.
- For an ideal gas, Z = 1 and it is independent of temperature and pressure.
- The deviations from the ideal behaviour of a real gas will be determined by the value of Z being greater or less than 1.
- The difference between unity and the value of the compressibility factor of a gas is a measure of the degree of non-ideality of the gas.
- For a real gas, the deviations from ideal behaviour depends on:
(i) Pressure
(ii) Temperature - This will be illustrated by examining the compressibility curves of some gases discussed below with the variation of pressure and temperature.
(i) Effect of Pressure Variation on Deviations:(ii) Effect of Temperature on Deviations:
From the above curves we can conclude that:(i) At low pressure and fairly high temperatures, real gases show nearly ideal behaviour and the ideal-gas equation is obeyed.
(ii) At low temperatures and sufficiently high pressures, a real gas deviates significantly from ideality and the ideal-gas equation is no longer valid.
(iii) The closer the gas is to the liquefaction point, the larger will be the deviation from the ideal behaviour.Greater is the departure of Z from unity, more is the deviation from ideal behaviour.
(i) When Z < 1, this implies that gas is more compressible.
(ii) When Z > 1, this means that gas is less compressible.
(iii) When Z = 1, the gas is ideal.
Vander Waal's Equation of State for a Real Gas
- The equation of state generated by Vander Waals in 1873 reproduces the observed behaviour with moderate accuracy.
- For n moles of gas, the Vander Waals equation is:
(V - nb) = nRT
where a and b are constants characteristic of a gas. - This equation can be derived by considering a real gas and converting it to an ideal gas.
1. Volume Correction
- We know that for an ideal gas PV = nRT.
- Now in a real gas, the molecular volume cannot be ignored and therefore, let us assume that 'b' is the volume excluded (out of the volume of container) for the moving gas molecules per mole of a gas. Therefore due to n moles of a gas, the volume excluded would be nb.
- Therefore, a real gas in a container of volume V has an only available volume of (V - nb) and this can be thought of, as an ideal gas in a container of volume (V - nb)
- The Vander Waals constant b (the excluded volume) is actually 4 times the volume of a single molecule. i.e. b = 4 NAV where NAxx Avogadro number.
∴ b = 4 x 6.023 x 1023 x
, where r is the radius of a molecule.
2. Pressure Correction
- Let us assume that the real gas exerts a pressure P. The molecules that exert the force on the container will get attracted by molecules of the immediate layer which are not assumed to be exerting pressure.
- It can be seen that the pressure the real gas exerts would be less than the pressure an ideal gas would have exerted. Therefore if a real gas exerts a pressure P, then an ideal gas would exert a pressure equal to P- p(where p is the pressure lost by the gas molecules due to attractions).
- This small pressure p would be directly proportional to the extent of attraction between the molecules which are hitting the container wall and the molecules which are attracting these.
Therefore,(concentration of molecules which are hitting the container's wall) and
(concentration of molecules which are attracting these molecules )
⇒ 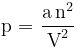 where a is the constant of proportionality which depends on the nature of the gas. A higher value of `a' reflects the increased attraction between gas molecules.
where a is the constant of proportionality which depends on the nature of the gas. A higher value of `a' reflects the increased attraction between gas molecules.
3. The Constants a and b
Vander Waals constant for attraction 'a' and volume 'b' are characteristic for a given gas. Some salient features of 'a' and 'b' are:
- For a given gas Vander Waal's constant of attraction 'a' is always greater than Vander Waals constant of volume 'b'.
- The gas having higher value of 'a' can be liquified easily and therefore H2 and He are not liquified easily.
- The units of a = litre2 atm mole-2 and that of b = litre mole-1
- The numerical values of a and b are in the order of 10-1 to 10-2 to 10-4 respectively.
- Higher is the value of `a' for a given gas, easier is the liquefaction.
4. Explanation of Deviation by Vander Waal's Equation
- At lower pressure: 'V' is large and 'b' is negligible in comparison with V.
Then Vander Waals equation reduces to:⇒
⇒⇒ z =
= 1 -
or PV < RT at low pressure (below Boyle temperature), this accounts for the dip in PV vs P isotherm at low pressure. - At fairly high pressures:
may be neglected in comparison with P.
The Vander Waals equation becomes:
P ( V-b) = RT ⇒ PV - Pb = RT
PV = RT + Pb ⇒ z = 1 +[∵ z =
]
or PV > RT at higher pressure (above Boyle temperature), this accounts for the rising parts of the PV vs P isotherm at high pressures. - At very low pressure: V becomes so large that both b and a become negligible and the Vander Waals equation reduces to PV = RT
At extremely low pressure (at Boyle temperature), this shows why gases approach ideal behaviour at very low pressures. - Hydrogen and Helium: These are two lightest gases known. Their molecules have very small masses. The attractive forces between such molecules will be extensively small. So
is negligible even at ordinary temperatures. Thus PV > RT.
Other Forms Representation of Deviation from Ideal Gas
- Dieterici Equation: P (V - nb) = n R T ea/VRT (for `n' mole of a gas)
- Berthelot Equation:
(V - nb) = n R T
- Virial Equation Of State For 1 Mole Of Gas:
z == 1 + B *
+ C *
+ D *
+ ..............
B, second virial coefficient , temperature-dependent = b - (a/RT)
C, third virial coefficient, temperature-dependent = b2
Example: The compressibility factor for 1 mole of a van der Waals gas at 0xC and 100 atm pressure is found to be 0.5. Assuming that the volume of a gas molecule is negligible, calculate the van der Waals constant, a.
Sol. For 1 mole of the gas,
Z = ⇒ 0.5 =
; V = 0.112 L
Neglecting b, van der Waals equation reduces to
or pV + = RT
or 100 x 0.112 + = .0821 x 273
a = 1.25 L2atm mol-2
Critical Phenomenon & Liquefaction of Gases
- The phenomena of converting gas into liquid is known as liquefaction.
- The liquefaction of gas is achieved by controlling P and T as follows:
(i) Increasing Pressure: An increase in pressure results in an increase in attraction among molecules.
(ii) Decreasing Temperature: A decrease in temperature results in a decrease in the kinetic energy of molecules. - Critical Temperature (Tc): It is defined as the characteristic temperature for a given gas below which a continuous increase in pressure will bring liquefaction of gas and above which no liquefaction is noticed although pressure may be increased.
Example: Tc for CO2 is 31.2°C.
TC = - Critical Pressure (Pc): It is defined as the minimum pressure applied on 1 mole of gas placed at the critical temperature, to just liquefy the gas
PC = - Critical Volume (Vc): The volume occupied by 1 mole of gas placed at critical conditions.
VC = 3b (i.e. P = Pc and T = Tc)
Collision Parameters
- Mean Free Path
=
(
= coefficient of viscosity)
=
k = Boltzman constant ;= collision diameter.
- Collision Frequency (z): no. of collision taking place per second per unit volume.
- Collision Diameter: Closest distance between the centre of two molecules that are participating in the collision.
- Relative Humidity (RH) :
At a given temperature, RH = - Loschmidth Number: The number of molecules present in 1 cc of gas (or vapour) at STP.
Its value is 2.617 × 1019 molecules per cc.
|
365 videos|701 docs|149 tests
|
FAQs on The Gaseous State - General Awareness - Bank Exams
| 1. What are some examples of measurable properties of gases? |  |
| 2. How is the ideal gas equation derived? |  |
| 3. What is Dalton's Law of Partial Pressure? |  |
| 4. How does Graham's Law of Diffusion relate to the movement of gases? |  |
| 5. What are deviations from ideal gas behavior? |  |

















