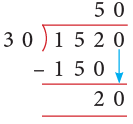The Transport Museum Class 4 Notes Maths Chapter 13 Free PDF
Welcome, explorers! Get ready for an exciting journey into the world of numbers as we visit the amazing Transport Museum.
Just like the museum is filled with fascinating vehicles, this chapter is packed with interesting ways to understand multiplication and division. Let's start our adventure!
Mystery Matrix
- Imagine you're a detective, and you've found a secret grid – a Mystery Matrix!
- Your mission, should you choose to accept it, is to fill in the missing numbers.
- In the first one, we need to fill the yellow boxes with single-digit numbers (these are our multiplicands and multipliers).
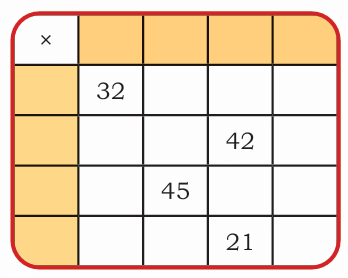
- When we multiply the number at the start of a row by the number at the top of a column, we get the product in the white box where they meet.
- Some products are already given to help us!
We see numbers like 32, 42, 45, and 21 in the white boxes. We need to figure out the single-digit numbers in the yellow row and column that multiply to give these products.
For example, to get 42, we could use 6 and 7 (6 × 7 = 42). To get 21, we could use 3 and 7 (3 × 7 = 21).
By looking at the relationships, we can deduce the numbers. If the row with 21 has a 3, and the column has a 7, does that work for 42 in the same column?
Yes, if the row for 42 has a 6 (6 x 7 = 42).
Keep going like this to solve the puzzle!
So the top row is: 8, 6, 3
The left column is: 4, 7, 9, 7
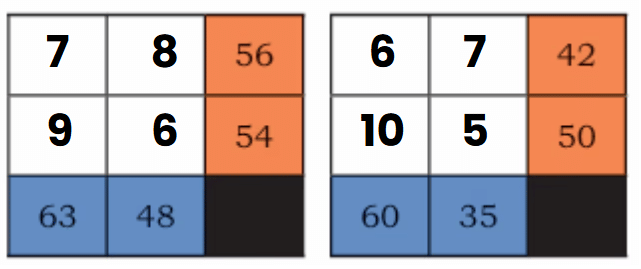
The second type of matrix gives us the products of entire rows (in orange boxes) and columns (in blue boxes).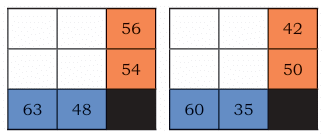 We need to fill in the grid so that the numbers in each row multiply to the orange number, and the numbers in each column multiply to the blue number. It's like a multiplication sudoku!
We need to fill in the grid so that the numbers in each row multiply to the orange number, and the numbers in each column multiply to the blue number. It's like a multiplication sudoku!
Here is the answer given below:
Times-10
Multiplying by 10 is like having a magic wand! It makes numbers bigger in a very predictable way.
When we multiply a number by 10, we are essentially creating groups of ten.
2 × 10: This means 2 groups of 10. That's 10 + 10 = 20. We can say it's 2 Tens, which equals 20.
5 × 10: This means 5 groups of 10. That's 10 + 10 + 10 + 10 + 10 = 50. We can say it's 5 Tens, which equals 50.
8 × 10: This means 8 groups of 10. That's 8 Tens, which equals 80.
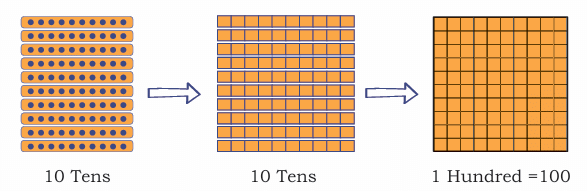
What happens when we multiply 10 by 10?
That's 10 groups of 10, which makes 10 Tens.
Constructing Tables
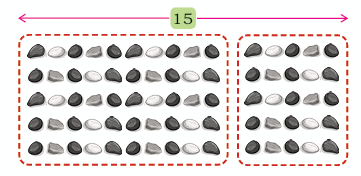
Remember playing with pebbles? They can help us understand multiplication tables too! Below given image shows an arrangement of pebbles, 5 rows with 15 pebbles in each row.
How many pebbles are there in total? We need to find 5 × 15.
Split the 15 pebbles in each row into a group of 10 and a group of 5.
So, 5 × 15 becomes (5 × 10) + (5 × 5).
5 × 10 = 50
5 × 5 = 25
Total = 50 + 25 = 75 pebbles!
We can use this splitting method to build multiplication tables. Let's try constructing the times-15 table, using the pebble arrangement or just the splitting idea:
1 × 15 = 1 × (10 + 5) = (1 × 10) + (1 × 5) = 10 + 5 = 15
2 × 15 = 2 × (10 + 5) = (2 × 10) + (2 × 5) = 20 + 10 = 30
3 × 15 = 3 × (10 + 5) = (3 × 10) + (3 × 5) = 30 + 15 = 45
...and so on!

Also,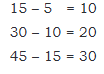
What do you notice in the above image?
The numbers in the times-15 table are three times the numbers in the times-5 table (since 15 is 3 times 5). Also, notice the difference between numbers in the times-15 table and times-10 table is 10!
Making tables by splitting into equal groups
Here's another cool strategy: splitting into equal groups!
Let's understand with an example. Here is an arrangement of wheels. To count the total number of wheels, Tara splits them into two equal groups.
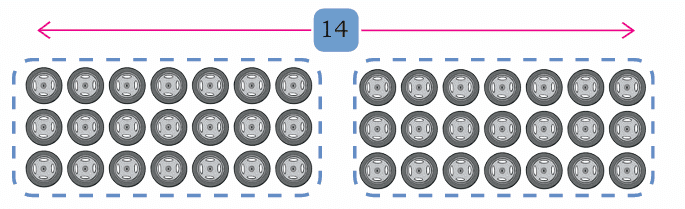
To find 3 × 14, Tara splits the 14 wheels in each row into two equal groups of 7.
So, 3 × 14 becomes (3 × 7) + (3 × 7).
3 × 7 = 21
Total = 21 + 21 = 42 wheels!
Notice that 21 + 21 is the same as doubling 21.
Similarly, for 6 × 14:
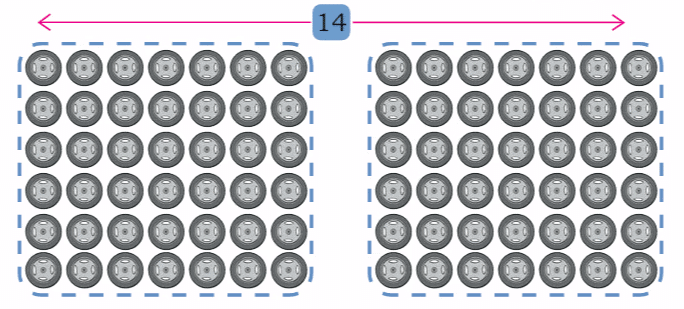
Split 14 into 7 and 7.
⇒ 6 × 14 becomes (6 × 7) + (6 × 7).
⇒ 6 × 7 = 42
⇒ Total = 42 + 42 = 84 wheels! This is the same as doubling 42. We can see that 6 x 14 is double of 6 x 7, because 7 is double of 14!
We can use this splitting and doubling method to construct other tables, like the times-14 table.
Multiples of 10
We saw how easy multiplying by 10 is. Let's practice more!
For example: 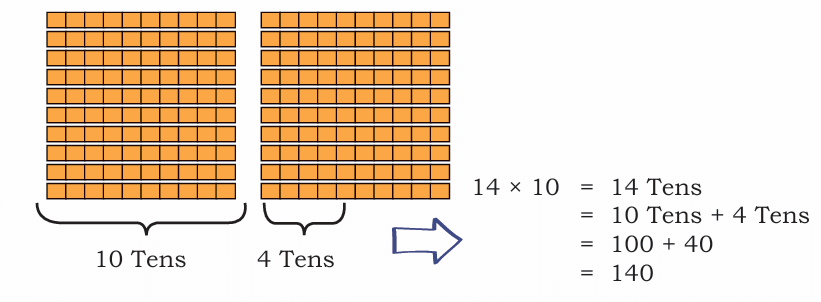
15 × 10 = 15 Tens = 150
16 × 10 = 16 Tens = 160
26 × 10 = 26 Tens = 20 Tens + 6 Tens = 200 + 60 = 260
Multiplying by Multiples of 10:
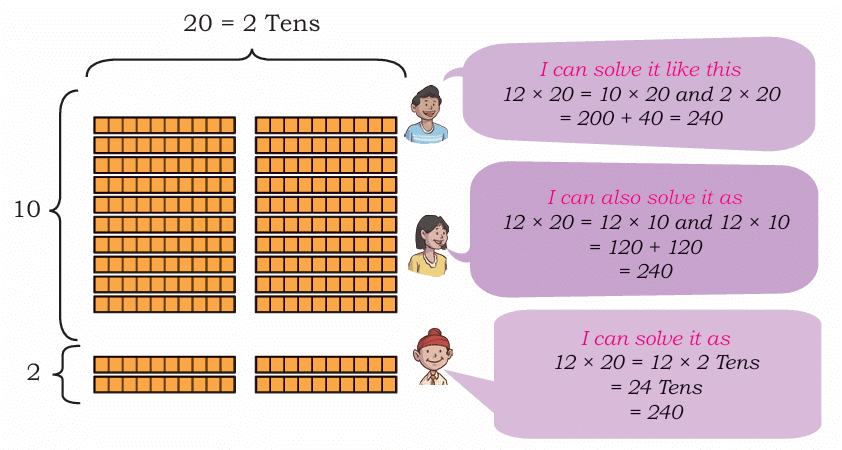
What about problems like 12 × 20?
We know 20 is 2 Tens (or 2 × 10). So, 12 × 20 is like 12 × 2 × 10.
Method 1: 12 × 20 = (10 × 20) + (2 × 20) = 200 + 40 = 240
Method 2: 12 × 20 = (12 × 10) + (12 × 10) = 120 + 120 = 240
Method 3: 12 × 20 = 12 × 2 Tens = 24 Tens = 240

A Day at the Transport Museum
Amala, Raahi, and Farzan are visiting the Transport Museum! It's full of old vehicles.

Toy Train: Raahi spots a toy train with 15 coaches. Each coach can seat 14 children. How many children can fit in the train?
We need to find 15 × 14.
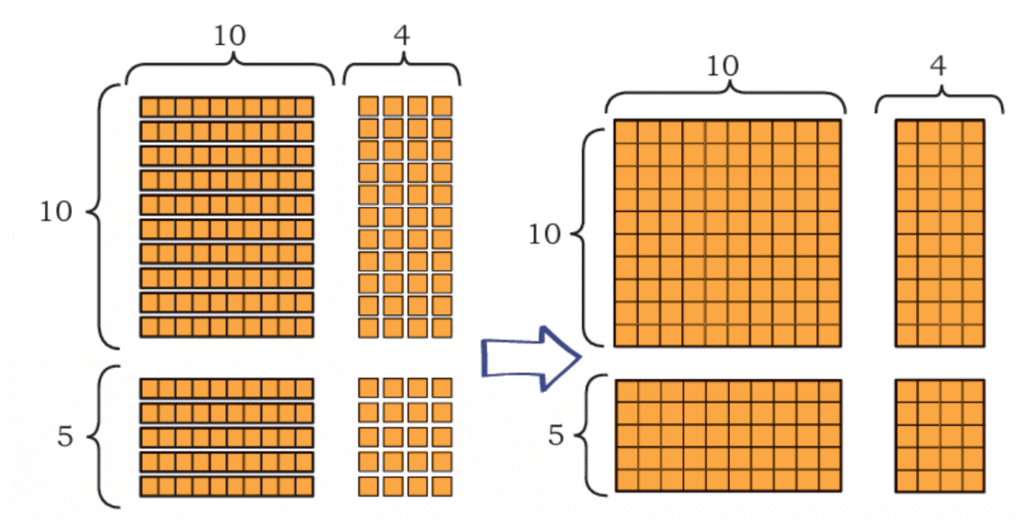
Let's use the splitting method (like the pebbles!):
15 × 14 = 15 × (10 + 4)
= (15 × 10) + (15 × 4)
= 150 + (10 × 4 + 5 × 4)
= 150 + (40 + 20)
= 150 + 60
= 210
So, 210 children can be seated in the toy train.
Now, Raahi wonders: If her school has 324 children, and each coach seats 14 children, how many coaches do they need?
We need to find:
324 ÷ 14
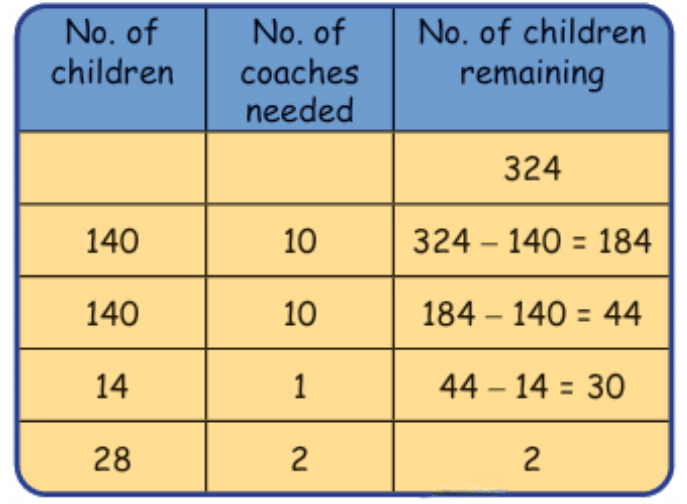
Let’s use subtraction to solve it step-by-step: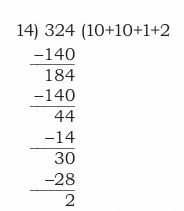
So far we used:
10 + 10 + 3 = 23 coaches
And we still have 2 children left
Such remaining number in a division problem is called ‘remainder’.
Multiples of 100
Remember 10 × 10 = 100? Multiplying by 100 is also straightforward.
2 × 100 = 2 Hundreds = 200
5 × 100 = 5 Hundreds = 500
What happens when we put 10 Hundreds together?
10 × 100 = 10 Hundreds = 1 Thousand = 1000

11 × 100 = 11 Hundreds = 10 Hundreds + 1 Hundred = 1000 + 100 = 1100
20 × 100 = 20 Hundreds = 2 × 10 Hundreds = 2 × 1000 = 2000
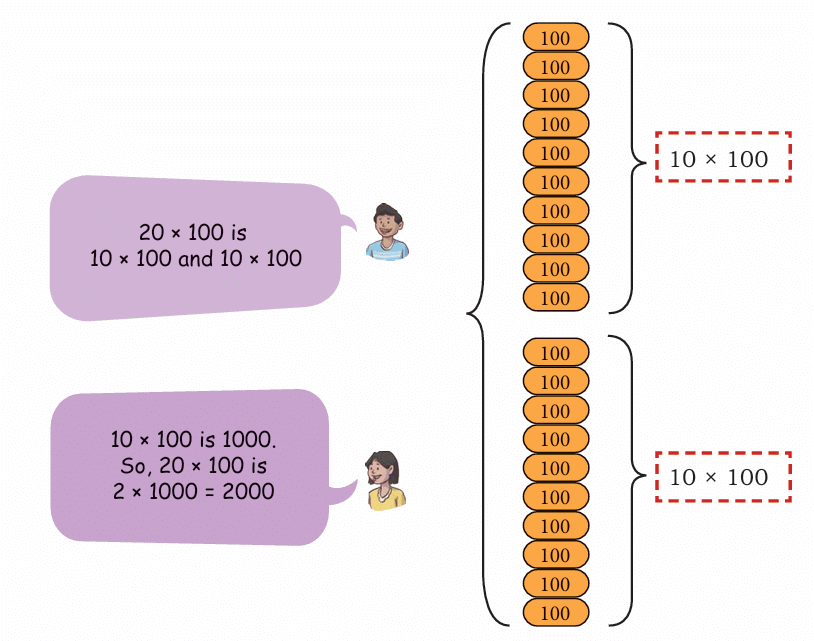
Pattern: To multiply by 100, just add two zeros to the end of the number!
Multiplying by 200 (and other hundreds):
Let's find 11 × 200.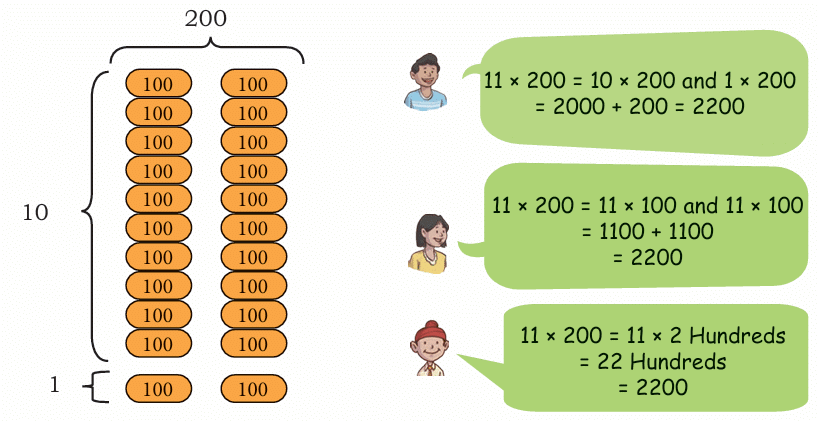
We know 200 is 2 Hundreds (or 2 × 100).
Method 1: 11 × 200 = (10 × 200) + (1 × 200) = 2000 + 200 = 2200
Method 2: 11 × 200 = (11 × 100) + (11 × 100) = 1100 + 1100 = 2200
Method 3: 11 × 200 = 11 × 2 Hundreds = 22 Hundreds = 2200
Now, Amala is fascinated to read this information in the aeroplane section of the transport museum.
Amala wonders how many people travelled the first week of this ‘Vande Bharat Mission’.
64 × 152
To make it easier, we break the numbers into parts:
64 = 60 + 4
152 = 100 + 50 + 2
Now we multiply each part like a grid or area box.
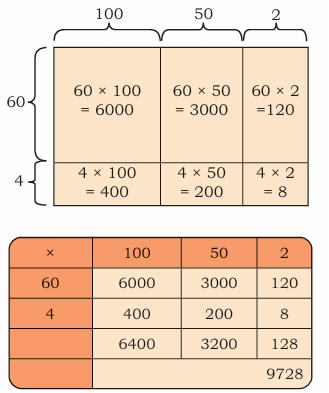
9728 people traveled in the first week of the Vande Bharat Mission.
Farzan notices the famous snake boat from Kerela. The technique for making these boats is 800 years old. Vallam kali (the snake-boat race) is held during the monsoon season between July and September and concludes with Onam, the harvest festival. These boats are 30 to 35 metres long and can be peddled by 64 –128 people.  In a particular race, 960 participants volunteered. Each boat is pedalled by 64 people. How many boats will be needed?
In a particular race, 960 participants volunteered. Each boat is pedalled by 64 people. How many boats will be needed?
Sol: We have to find 960 ÷ 64 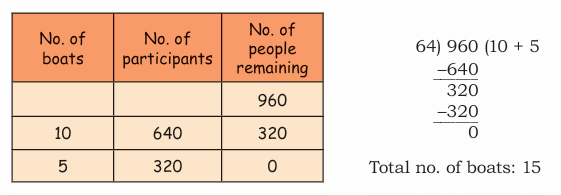
Dividing by 10 and 100
A Farmer’s Rice Problem
A farmer has a lot of rice and wants to pack it into sacks. Each sack can hold 10 kg of rice.
Now, let’s answer some questions!
a) If the farmer has 60 kg of rice, how many sacks does he need?
We divide 60 by 10:
60 ÷ 10 = 6
So, he needs 6 sacks.
b) If the farmer has 600 kg of rice, how many sacks does he need?
600 ÷ 10 = 60
He needs 60 sacks.
What if each sack holds 100 kg?
Now the question becomes:
600 ÷ 100 = ?
The answer is 6 sacks.
So, if sacks are bigger (100 kg each), you need fewer of them.
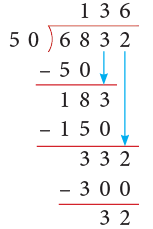
Example 1: Divide 6832 by 50.
Solution:
Thus, 6832 ÷ 50 gives Q = 136 and R = 32.
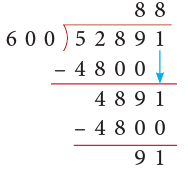
Example 2: Divide 52891 by 600.
Solution:
Thus, 52891 ÷ 600 gives Q = 88 and R = 91.
Chinnu's Coins
A Visit to the Amusement Park
Five friends are going to an amusement park.
Each ticket costs ₹750.
But here’s the fun part:
Each friend brings only one kind of note or coin!
Let’s see what they brought:
Bujji – all ₹200 notes
Munna – all ₹50 notes
Balu – all ₹20 notes
Chinnu – all ₹5 coins
Sansu – all ₹2 coins
a) How many notes/coins does each child need?
Let’s divide ₹750 by the value they have:
1. Bujji:
₹750 ÷ ₹200 = 3 notes (₹600), but that’s not enough
We need one more ₹150
→ 3 notes of ₹200 = ₹600
→ Still short by ₹150 → Can’t pay exactly
Let’s try 4 notes:
4 × ₹200 = ₹800 → too much
Not exact.
So Bujji cannot pay exactly.
2. Munna:
₹750 ÷ ₹50 = 15 notes
Munna can pay exactly.
3. Balu:
₹750 ÷ ₹20 = 37.5 notes
Half a note isn't possible.
So Balu cannot pay exactly.
4. Chinnu:
₹750 ÷ ₹5 = 150 coins
That’s a lot! But it works.
Chinnu can pay exactly.
5. Sansu:
₹750 ÷ ₹2 = 375 coins
Sansu can also pay exactly.
b) Who will NOT receive any change?
That means they give the exact amount of ₹750.
Munna, Chinnu, and Sansu give exact amounts.
Bujji and Balu will not be able to pay exactly.
c) How long would the cashier take to count Chinnu’s coins?
Chinnu has to pay ₹750.
He is using only ₹5 coins.
₹750 ÷ ₹5 = 150 coins.
If the cashier takes about 2 seconds to count each coin, then:
150 coins × 2 seconds = 300 seconds
→ 300 seconds ÷ 60 = 5 minutes
Conclusion:
- Students learn to divide a total amount of money by the value of a note or coin to find out how many are needed.
- They explore whether the amount can be paid exactly using the notes or coins, or if there's leftover money or extra.
- It shows how multiplication and division are connected — if 15 × ₹50 = ₹750, then ₹750 ÷ ₹50 = 15.
Example 3: The sports teacher is cutting ribbons for the sports medals. How many ribbons of 30 cm length can the teacher get from a roll of ribbon that is 1520 cm long?
Solution:
At first, we divide 1520 by 30.
- Here, we ignore the remainder as the question asks for the number of pieces exactly 30 cm in length.
Thus, the teacher will get 50 pieces each of 30 cm length.
|
54 videos|186 docs|14 tests
|
FAQs on The Transport Museum Class 4 Notes Maths Chapter 13 Free PDF
| 1. What is a multiplication matrix and how is it used in mathematics? |  |
| 2. How do you multiply a number by 10, and why is it important? |  |
| 3. What are the key steps in learning the times-15 table? |  |
| 4. What does splitting and doubling mean in multiplication, and how can it be applied? |  |
| 5. How can I effectively multiply by higher numbers like 20, 50, and 100? |  |