Thousands Around Us Class 4 Notes Maths Chapter 4 Free PDF
| Table of contents |

|
| Introduction |

|
| Place Value System |

|
| One Thousand(1000) |

|
| Grouping and Regrouping |

|
| Numbers Beyond 1000 ( One Thousand) |

|
| Comparing Numbers |

|
| Solved Examples |

|
Introduction
In this chapter, we will explore the fascinating world of large numbers, particularly focusing on thousands and how they relate to our daily lives. From counting people at community events to understanding place values, we'll discover how numbers up to and beyond 1000 are represented in the Indian number system.
Thousands of Stars in the Night Sky
If you look at the night sky, you will find thousands of twinkling stars. They show us how large the number thousands really is!
Let's begin with a practical example!
- Jaspreet and Gulnaz are organizing a langar (community lunch) at their neighborhood Gurudwara.
- They expect around one thousand (1000) people to attend.
- Throughout the event, they keep track of how many people come at different times: 52 people, 145 people, 325 people and 508 people.
 Community lunch organised by Jaspreet and Gulnaz
Community lunch organised by Jaspreet and Gulnaz - By the end of the day, they need to count how many people in total were served food.
This requires understanding how to work with numbers in the hundreds and thousands.
Place Value System
The Indian number system, which was discovered in India around 2000 years ago, allows us to write all numbers using just ten symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. This system is now used around the world!
A place value chart helps us see how much each digit in a number is worth based on where it is located.

Example: How can we break down the number 4567 using the Indian place value system?
Sol: We break the number from right to left like this:

4 thousands = 4,000
5 hundreds = 500
6 tens = 60
7 ones = 7
So,
4,567 = 4,000 + 500 + 60 + 7




One Thousand(1000)
We can visualize numbers using Dienes Blocks (also known as Base-10 Blocks):
Place Value Dienes Blocks
Dienes blocks showing representation of numbers with ones, tens, hundreds, and thousands.
One (1) - represented by a small cube
Ten (10) - represented by a rod of 10 small cubes
Hundred (100) - represented by a flat square of 10×10 small cubes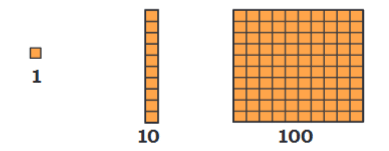
Thousand (1000) - represented by a large cube of 10×10×10 small cubes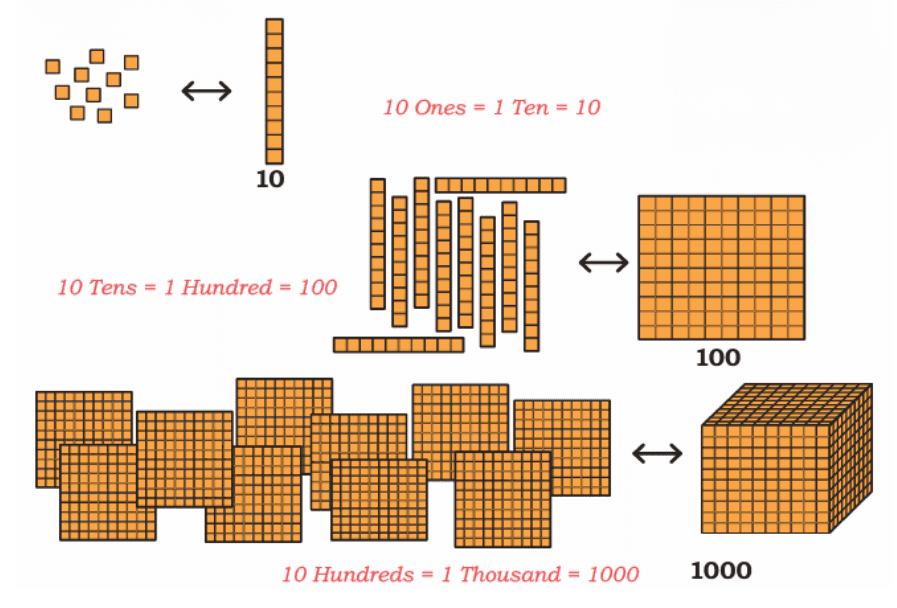
This helps us understand the relationship between different place values:
10 Ones = 1 Ten
10 Tens = 1 Hundred
10 Hundreds = 1 Thousand
Grouping and Regrouping
1. When we have more than 9 in any place value, we need to regroup:
10 Ones → 1 Ten
10 Tens → 1 Hundred
10 Hundreds → 1 Thousand
2. Regrouping ones into tens and tens into hundreds using base 10 blocks
For example:
14 Ones = 1 Ten + 4 Ones
23 Ones = 2 Tens + 3 Ones
106 = 1 Hundred + 0 Tens + 6 Ones (or 10 Tens + 6 Ones)
Circle as many groups of 10 Ones or 10 Tens as possible. Write the final number against the following pictures.
a)
b)
c)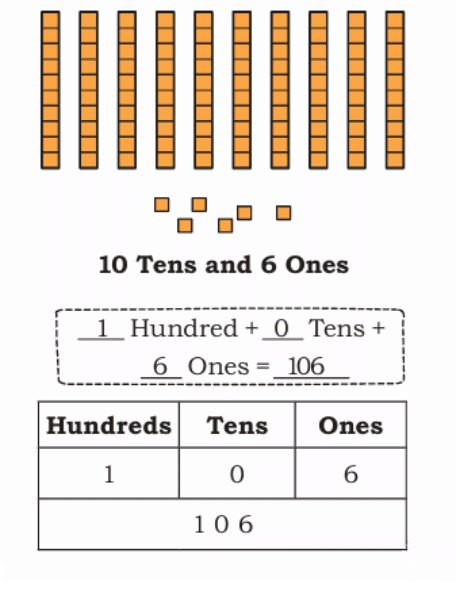
Numbers Beyond 1000 ( One Thousand)
Let’s learn about big numbers — numbers that are more than 1000!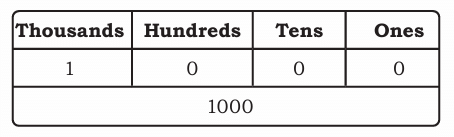
What is 1000?
1000 is made up of:
1 Thousand
0 Hundreds
0 Tens
0 Ones
So, 1000 = 1 thousand + 0 hundred + 0 ten + 0 one
We use special blocks called Dienes Blocks to show numbers. But drawing big blocks is hard! So, we use tokens to show the same numbers.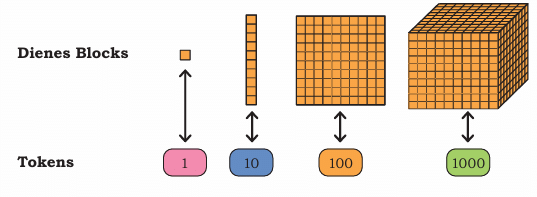
Let’s Make the Number
1001
Look at this:
We have 10 orange tokens of 100 each → 100 × 10 = 1000
And 1 pink token → 1
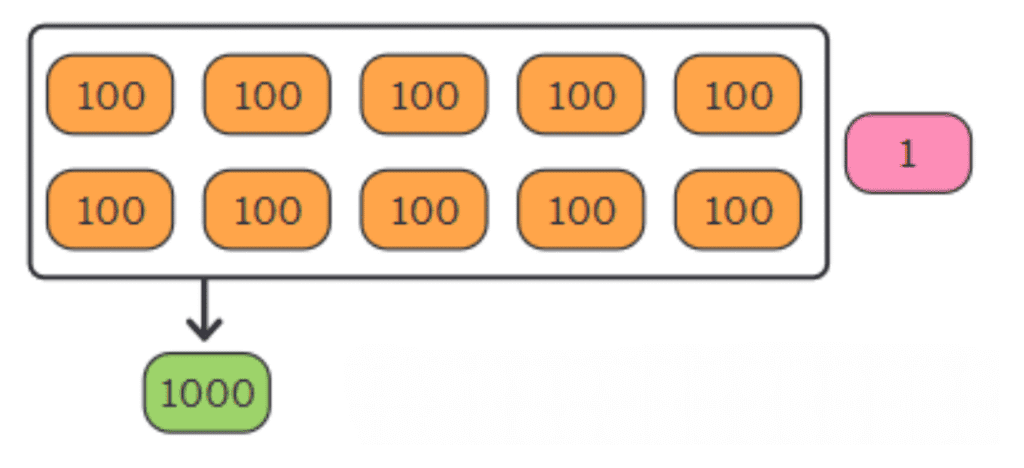 That means: 1000 + 1 = 1001
That means: 1000 + 1 = 1001
Let’s Write It in the Place Value Table:
1 Thousand + 0 Hundred + 0 Ten + 1 One = 1001
Comparing Numbers
Comparing numbers means looking at two numbers and finding out which one is greater, smaller, or if they are equal.
We use three special signs to compare:
Greater than ( > )
Example: 7 > 5 (7 is bigger than 5)Less than ( < )
Example: 3 < 9 (3 is smaller than 9)Equal to ( = )
Example: 4 = 4 (Both numbers are same)
Let’s compare 3012 and 3102.
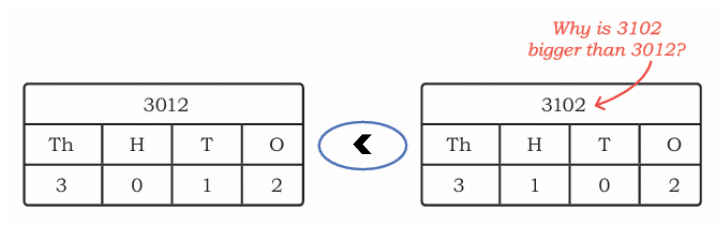
Thousands:
Both numbers have 3 thousands. So we go to the next digit.
Hundreds:
- 3012 has 0 hundreds
- 3102 has 1 hundred
Since 1 hundred is more than 0 hundreds,
So, 3102 > 3012
Q1: Compare the numbers 425 and 452. Which one is larger?
Sol: Step 1: Both numbers have 3 digits, so we need to compare the digits.
Step 2: Compare the hundreds digit: Both have 4 in the hundreds place.
Step 3: Compare the tens digit: 2 in 425 and 5 in 452.
Since 5 > 2, we know that 452 > 425.
Therefore, 452 is larger than 425.
Q2: Arrange the numbers 789, 798, 879, 897, 978, 987 in ascending order (smallest to largest).
Sol: Ascending order means arranging numbers from the smallest to the largest.
Let’s arrange these numbers:789, 798, 879, 897, 978, 987
Step 1: Look at the Hundreds Place
Hundreds PlaceAll numbers start with 7, 8, or 9.
789 and 798 start with 7 → smallest group
879 and 897 start with 8
978 and 987 start with 9 → biggest group
Step 2: Compare numbers within each group
Group starting with 7:
789 < 798
Group starting with 8:
879 < 897
Group starting with 9:
978 < 987

Solved Examples
Example 1: Write the number 1,234 in expanded form and identify the place value of each digit.
Sol: Step 1: Identify the place value of each digit.
1 is in the thousands place
2 is in the hundreds place
3 is in the tens place
4 is in the ones place
Step 2: Write the expanded form by multiplying each digit by its place value.
1 × 1000 = 1000
2 × 100 = 200
3 × 10 = 30
4 × 1 = 4
Step 3: Add all the values to get the expanded form.
1,234 = 1000 + 200 + 30 + 4
Example 2: Arrange the numbers 1,025, 1,205, 1,052, and 1,520 in descending order (largest to smallest).
Sol: Step 1: Compare the thousands digit.
All numbers have 1 in the thousands place, so we need to compare the hundreds digit.
Step 2: Compare the hundreds digit.
1,025 has 0 in the hundreds place
1,205 has 2 in the hundreds place
1,052 has 0 in the hundreds place
1,520 has 5 in the hundreds place
Since 5 > 2 > 0, we know that 1,520 is the largest, followed by 1,205.
Step 3: For numbers with the same hundreds digit (1,025 and 1,052), compare the tens digit.
1,025 has 2 in the tens place
1,052 has 5 in the tens place
Since 5 > 2, we know that 1,052 > 1,025.
Step 4: Arrange all numbers in descending order:
1,520, 1,205, 1,052, 1,025
Example 3: Find the next three numbers in the pattern: 825, 850, 875, ...
Sol: Step 1: Identify how the numbers change from one to the next.
From 825 to 850: The number increases by 25
From 850 to 875: The number increases by 25
Step 2: Apply the same pattern to find the next three numbers.
After 875, adding 25 gives us 900
After 900, adding 25 gives us 925
After 925, adding 25 gives us 950
So the next three numbers in the pattern are 900, 925, and 950.
By understanding these concepts, you can confidently work with larger numbers and apply this knowledge to solve real-world problems. Remember, mathematics is not just about numbers; it's about understanding the patterns and relationships that help us make sense of the world around us.
|
54 videos|186 docs|14 tests
|
FAQs on Thousands Around Us Class 4 Notes Maths Chapter 4 Free PDF
| 1. What are the basic concepts of understanding numbers up to 1000? |  |
| 2. How do we compare and order numbers up to 1000? |  |
| 3. Can you give some real-life examples of using thousands? |  |
| 4. How can we use a number line to represent numbers up to 1000? |  |
| 5. What are some ways to break up the number 1000 into smaller parts? |  |





















