ICAI Notes: Time Value of Money- 1 - CA Foundation PDF Download
LEARNING OBJECTIVES
After studying this chapter students will be able to understand:-
- The concept of interest, related terms and computation thereof;
- Difference between simple and compound interest;
- The concept of annuity;
- The concept of present value and future value;
- Use of present value concept in Leasing, Capital expenditure and Valuation of Bond.
- Calculation of Returns.
- Compound Annual Growth Rate (CAGR).
4.1 INTRODUCTION
People earn money for spending it on housing food clothing education entertainment etc.
Sometimes extra expenditures have also to be met with. For example there might be a marriage in the family; one may want to buy house, one may want to set up his or her business, one may want to buy a car and so on. Some people can manage to put aside some money for such expected and unexpected expenditures. But most people have to borrow money for such contingencies. From where they can borrow money?
Money can be borrowed from friends or money lenders or Banks. If you can arrange a loan from your friend it might be interest free but if you borrow money from lenders or Banks you will have to pay some charge periodically for using money of money lenders or Banks. This charge is called interest.
Let us take another view. People earn money for satisfying their various needs as discussed above. After satisfying those needs some people may have some savings. People may invest their savings in debentures or lend to other person or simply deposit it into bank. In this way they can earn interest on their investment.
Most of you are very much aware of the term interest. Interest can be defined as the price paid by a borrower for the use of a lender’s money.
We will know more about interest and other related terms later.
4.2 WHY IS INTEREST PAID?
Now question arises why lenders charge interest for the use of their money. There are a variety of reasons. We will now discuss those reasons.
1. Time value of money: Time value of money means that the value of a unity of money is different in different time periods. The sum of money received in future is less valuable than it is today. In other words the present worth of rupees received after some time will be less than a rupee received today. Since a rupee received today has more value rational investors would prefer current receipts to future receipts. If they postpone their receipts they will certainly charge some money i.e. interest.
2. Opportunity Cost: The lender has a choice between using his money in different investments. If he chooses one he forgoes the return from all others. In other words lending incurs an opportunity cost due to the possible alternative uses of the lent money.
3 . Inflation: Most economies generally exhibit inflation. Inflation is a fall in the purchasing power of money. Due to inflation a given amount of money buys fewer goods in the future than it will now. The borrower needs to compensate the lender for this.
4. Liquidity Preference: People prefer to have their resources available in a form that can immediately be converted into cash rather than a form that takes time or money to realize.
5. Risk Factor: There is always a risk that the borrower will go bankrupt or otherwise default on the loan. Risk is a determinable factor in fixing rate of interest.
A lender generally charges more interest rate (risk premium) for taking more risk.
4.3 DEFINITION OF INTEREST AND SOME OTHER RELATED TERMS
Now we can define interest and some other related terms.
4.3.1 Interest: Interest is the price paid by a borrower for the use of a lender’s money. If you borrow (or lend) some money from (or to) a person for a particular period you would pay (or receive) more money than your initial borrowing (or lending). This excess money paid (or received) is called interest. Suppose you borrow (or lend) Rs.50000 for a year and you pay (or receive) Rs.55000 after one year the difference between initial borrowing (or lending) Rs.50000 and end payment (or receipts) Rs.55000 i.e. Rs.5000 is the amount of interest you paid (or earned).
4.3.2 Principal: Principal is initial value of lending (or borrowing). If you invest your money the value of initial investment is also called principal. Suppose you borrow ( or lend) Rs.50000 from a person for one year. Rs.50000 in this example is the ‘Principal.’ Take another example suppose you deposit Rs.20000 in your bank account for one year. In this example Rs.20000 is the principal.
4.3.3 Rate of Interest: The rate at which the interest is charged for a defined length of time for use of principal generally on a yearly basis is known to be the rate of interest. Rate of interest is usually expressed as percentages. Suppose you invest Rs.20000 in your bank account for one year with the interest rate of 5% per annum. It means you would earn Rs.5 as interest every Rs.100 of principal amount in a year.
Per annum means for a year.
4.3.4 Accumulated amount (or Balance): Accumulated amount is the final value of an investment. It is the sum total of principal and interest earned. Suppose you deposit Rs.50000 in your bank for one year with a interest rate of 5% p.a. you would earn interest of Rs.2500 after one year. (method of computing interest will be illustrated later). After one year you will get Rs.52500 (principal+ interest), Rs.52 500 is amount here.
Amount is also known as the balance.
4.4 SIMPLE INTEREST AND COMPOUND INTEREST
Now we can discuss the method of computing interest. Interest accrues as either simple interest or compound interest. We will discuss simple interest and compound interest in the following paragraphs:
4.4.1 Simple Interest: Now we would know what is simple interest and the methodology of computing simple interest and accumulated amount for an investment (principal) with a simple rate over a period of time. As you already know the money that you borrow is known as principal and the money that you pay for using somebody else’s money is known as interest. The interest paid for keeping Rs.100 for one year is known as the rate percent per annum. Thus if money is borrowed at the rate of 8% per annum the interest paid for keeping Rs.100 for one year is Rs.8. The sum of principal and interest is known as the amount.
Clearly the interest you pay is proportionate to the money that you borrow and also to the period of time for which you keep the money; the more the money and the time the more the interest. Interest is also proportionate to the rate of interest agreed upon by the lending and the borrowing parties. Thus interest varies directly as principal time and rate.
Simple interest is the interest computed on the principal for the entire period of borrowing. It is calculated on the outstanding principal balance and not on interest previously earned. It means no interest is paid on interest earned during the term of loan.
Simple interest can be computed by applying following formulas:
I = P*i*t
A = P + I
= P + P*i*t
= P(1 + i*t)
I = A – P
Here
A = Accumulated amount (final value of an investment)
P = Principal (initial value of an investment)
i = annual interest rate.
I = Amount of Interest
t = time in years
Let us consider the following examples in order to see how exactly are these quantities related.
Example 1: How much interest will be earned on Rs.2000 at 6% simple interest for 2 years?
Solution: Required interest amount is given by
I = P × i × t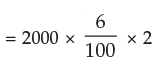
= Rs. 240
Example 2: Sania deposited Rs.50000 in a bank for two years with the interest rate of 5.5% p.a. How much interest would she earn?
Solution: Required interest amount is given by I = P × i × t
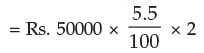
= Rs. 5500
Example 3: In example 2 what will be the final value of investment?
Solution: Final value of investment is given by A = P(1 + it)
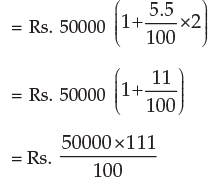
= Rs. 55500
Or
A = P + I
= Rs.(50000 + 5500)
= Rs. 55500
Example 4: Sachin deposited Rs.100000 in his bank for 2 years at simple interest rate of 6%.
How much interest would he earn? How much would be the final value of deposit?
Solution: (a) Required interest amount is given by
I = P × it
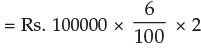
= Rs. 12000
(b) Final value of deposit is given by
A = P + I
= Rs. (100000 + 12000)
= Rs. 112000
Example 5: Find the rate of interest if the amount owed after 6 months is Rs.1050, borrowed amount being Rs.1000.
Solution: We know A = P + Pit
i.e. 1050 = 1000 + 1000 × i × 6/12
50 = 500 i
i = 1/10 = 10%
Example 6: Rahul invested Rs.70000 in a bank at the rate of 6.5% p.a. simple interest rate. He received Rs.85925 after the end of term. Find out the period for which sum was invested by Rahul.
Solution: We know A = P (1+it)
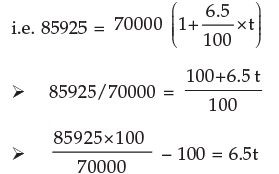
22.75 = 6.5t
t = 3.5 ∴ time = 3.5 years
Example 7: Kapil deposited some amount in a bank for 7 ½ years at the rate of 6% p.a. simple interest. Kapil received Rs.101500 at the end of the term. Compute initial deposit of Kapil.
Solution: We know A = P(1+ it)
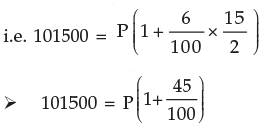
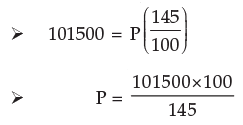
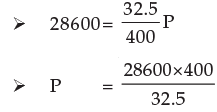
Initial deposit of Kapil = Rs.70000
Example 8: A sum of Rs.46875 was lent out at simple interest and at the end of 1 year 8 months the total amount was Rs.50000. Find the rate of interest percent per annum.
Solution: We know A = P (1 + it)
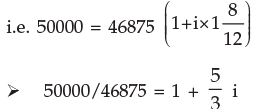
(1.067 – 1) × 3/5 = i
i = 0.04
rate = 4%
Example 9: What sum of money will produce Rs.28600 interest in 3 years and 3 months at 2.5% p.a. simple interest?
Solution: We know I = P × it
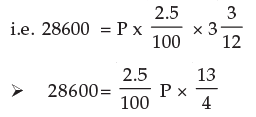

= Rs. 352000
Rs.352000 will produce Rs.28600 interest in 3 years and 3 months at 2.5% p.a. simple interest
Example 10: In what time will Rs.85000 amount to Rs.157675 at 4.5 % p.a.?
Solution: We know A = P (1 + it)
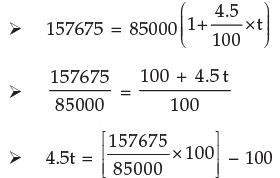
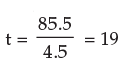
In 19 years Rs.85000 will amount to Rs.157675 at 4.5% p.a. simple interest rate.
4.4.2 Compound Interest:
We have learnt about the simple interest. We know that if the principal remains the same for the entire period or time then interest is called the simple interest.
However in practice the method according to which banks, insurance corporations and other money lending and deposit taking companies calculate interest is different. To understand this method we consider an example :
Suppose you deposit Rs.50000 in ICICI bank for 2 years at 7% p.a. compounded annually.
Interest will be calculated in the following way:
INTEREST FOR FIRST YEAR
I = Pit
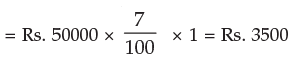
INTEREST FOR SECOND YEAR
For calculating interest for second year principal would not be the initial deposit. Principal for calculating interest for second year will be the initial deposit plus interest for the first year.
Therefore principal for calculating interest for second year would be
= Rs. 50000 + Rs. 3500
= Rs. 53500
Interest for the second year =Rs. 53500 × 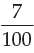 × 1
× 1
= Rs. 3745
Total interest = interest for first year + interest for second year
= Rs. (3500+3745)
= Rs. 7245
This interest is Rs. 245 more than the simple interest on Rs. 50000 for two years at 7% p.a. As you must have noticed this excess in interest is due to the fact that the principal for the second year was more than the principal for first year. The interest calculated in this manner is called compound interest.
Thus we can define the compound interest as the interest that accrues when earnings for each specified period of time added to the principal thus increasing the principal base on which subsequent interest is computed.
Example 11: Saina deposited Rs. 100000 in a nationalized bank for three years. If the rate of interest is 7% p.a. calculate the interest that bank has to pay to Saina after three years if interest is compounded annually. Also calculate the amount at the end of third year.
Solution: Principal for first year Rs. 100000
Interest for first year = Pit
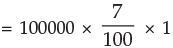
Principal for the second year = Principal for first year + interest for first year
= Rs. 100000 + Rs. 7000
= Rs. 107000
Interest for second year = 107000 × 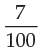 × 1
× 1
= Rs. 7490
Principal for the third year = Principal for second year + interest for second year
= 107000 + 7490
= 114490
Interest for the third year = Rs. 114490 × 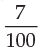 × 1
× 1
= Rs. 8014.30
Compound interest at the end of third year
= Rs. (7000 + 7490 + 8014.30)
= Rs. 22504.30
Amount at the end of third year
= Principal (initial deposit) + compound interest
= Rs. (100000 + 22504.30)
= Rs. 122504.30
Now we can summarize the main difference between simple interest and compound interest.
The main difference between simple interest and compound interest is that in simple interest the principal remains constant throughout whereas in the case of compound interest principal goes on changing at the end of specified period. For a given principal, rate and time the compound interest is generally more than the simple interest.
4.4.3 Conversion period: In the example discussed above the interest was calculated on yearly basis i.e. the interest was compounded annually. However in practice it is not necessary that the interest be compounded annually. For example in banks the interest is often compounded twice a year (half yearly or semi annually) i.e. interest is calculated and added to the principal after every six months. In some financial institutions interest is compounded quarterly i.e. four times a year. The period at the end of which the interest is compounded is called conversion period. When the interest is calculated and added to the principal every six months the conversion period is six months. In this case number of conversion periods per year would be two. If the loan or deposit was for five years then the number of conversion period would be ten.
Typical conversion periods are given below:
| Conversion period | Description | Number of conversion period in a year |
| 1 day | Compounded daily | 365 |
| 1 month | Compounded monthly | 12 |
| 3 months | Compounded quarterly | 4 |
| 6 months | Compounded semi annually | 2 |
| 12 months | Compounded annually | 1 |
4.4.4 Formula for compound interest: Taking the principal as P, the rate of interest per conversion period as i (in decimal), the number of conversion period as n, the accrued amount after n payment periods as An we have accrued amount at the end of first payment period
A1 = P + P i = P ( 1 + i ) ;
at the end of second payment period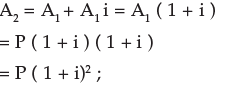
at the end of third payment period

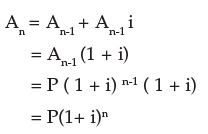
Thus the accrued amount An on a principal P after n conversion periods at i (in decimal) rate of interest per conversion period is given by
An = P (1 + i)n
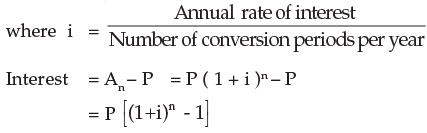
Computation of A shall be quite simple with a calculator. However compound interest table as well as tables for at various rates per annum with (a) annual compounding ; (b) monthly compounding and (c) daily compounding are available.
Example 12: Rs. 2000 is invested at annual rate of interest of 10%. What is the amount after two years if compounding is done (a) Annually (b) Semi-annually (c) Quarterly (d) monthly.
Solution: (a) Compounding is done annually Here principal P = Rs. 2000; since the interest is compounded yearly the number of conversion periods n in 2 years are 2. Also the rate of interest per conversion period (1 year) i is 0.10
An = P(1 + i)n
A2 = Rs. 2000 (1 + 0.1)2
= Rs. 2000 × (1.1)2
= Rs. 2000 × 1.21
= Rs. 2420
(b) For semiannual compounding
n = 2 × 2 = 4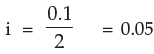
A4 = 2000 (1+0.05)4
= 2000×1.2155
= Rs. 2431
(c) For quarterly compounding
n = 4 × 2 = 8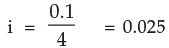
A8 = 2000 (1+ 0.025)8
= 2000 × 1.2184
= Rs. 2436.80
(d) For monthly compounding
n = 12 × 2 = 24, i = 0.1/12 = 0.00833
A 24 = 2000 (1 + 0.00833)24
= 2000 × 1.22029
= Rs. 2440.58
Example 13: Determine the compound amount and compound interest on Rs.1000 at 6% compounded semi-annually for 6 years. Given that (1 + i)n = 1.42576 for i = 3% and n = 12.
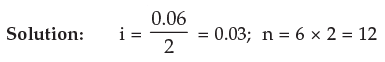
P = 1000
Compound Amount (A12) = P (1 + i)n
= Rs. 1000(1 + 0.03)12
= 1000 × 1.42576
= Rs. 1425.76
Compound interest = Rs. (1425.76 – 1000)
= Rs. 425.76
Example 14: Compute the compound interest on Rs. 4000 for 1½ years at 10% per annum compounded half- yearly.
Solution: Here principal P = Rs. 4000. Since the interest is compounded half-yearly the number of conversion periods in 1½ years are 3. Also the rate of interest per conversion period (6 months) is 10% x 1/2 = 5% (0.05 in decimal).
Thus the amount An (in Rs.) is given by
An= P (1 + i)n
A3= 4000(1 + 0.05)3
= 4630.50
The compound interest is therefore Rs.(4630.50 - 4000)
= Rs.630.50
To find the Principal/Time/Rate
The Formula An = P(1 + i)n connects four variables An, P, i and n.
Similarly, C.I.(Compound Interest) =  connects C.I., P, i and n. Whenever three out of these four variables are given the fourth can be found out by simple calculations.
connects C.I., P, i and n. Whenever three out of these four variables are given the fourth can be found out by simple calculations.
Examples 15: On what sum will the compound interest at 5% per annum for two years compounded annually be Rs.1640?
Solution: Here the interest is compounded annually the number of conversion periods in two years are 2. Also the rate of interest per conversion period (1 year) is 5%.
n = 2 i = 0.05
We know
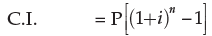
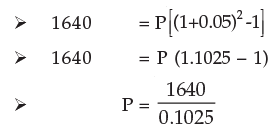
= 16000
Hence the required sum is Rs.16000.
Example 16: What annual rate of interest compounded annually doubles an investment in 7 years? Given that 21/7 = 1.104090
Solution: If the principal be P then An = 2P.
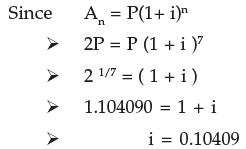
∴ Required rate of interest = 10.41% per annum
Example 17: In what time will Rs.8000 amount to Rs.8820 at 10% per annum interest compounded half-yearly?
Solution: Here interest rate per conversion period 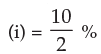 = 5% (= 0.05 in decimal)
= 5% (= 0.05 in decimal)
Principal (P) = Rs. 8000
Amount (An) = Rs. 8820
We know
An = P ( I + i )n
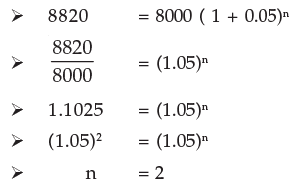
Hence number of conversion period is 2 and the required time = 2´6 months = 12 months = 1 year Example 18: Find the rate percent per annum if Rs.200000 amount to Rs.231525 in 1½ year interest being compounded half-yearly.
Solution: Here P = Rs. 200000
Number of conversion period (n) = 1½ × 2 = 3
Amount (A3) = Rs. 231525
We know that
A3 = P (1 + i)3
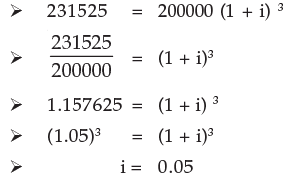
Interest rate per conversion period (six months) = 0.05 = 5%
Interest rate per annum = 5% × 2 = 10%
Example 19: A certain sum invested at 4% per annum compounded semi-annually amounts to Rs.78030 at the end of one year. Find the sum.
Solution: Here An = 78030
n = 2 × 1 = 2
i = 4 × 1/2 % = 2% = 0.02
P(in Rs.) = ?
We have
An = P(1 + i)n
A2 = P(1 + 0.02)2
78030 = P (1.02)2
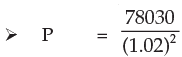
Thus the sum invested is Rs.75000.
Example 20: Rs.16000 invested at 10% p.a. compounded semi-annually amounts to Rs.18522.
Find the time period of investment.
Solution: Here P = Rs. 16000
An = Rs. 18522
i = 10 × 1/2 % = 5% = 0.05
n= ?
We have An = P(1 + i)n
Therefore time period of investment is three half years i.e. 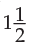 years.
years.
Example 21: A person opened an account on April, 2001 with a deposit of Rs.800. The account paid 6% interest compounded quarterly. On October 1 2001 he closed the account and added enough additional money to invest in a 6 month time-deposit for Rs. 1000, earning 6% compounded monthly.
(a) How much additional amount did the person invest on October 1?
(b) What was the maturity value of his time deposit on April 1 2002?
(c) How much total interest was earned?
Given that (1 + i)n is 1.03022500 for i=1½ % n=2 and (1+ i)n is 1.03037751 for i = ½ % and n = 6.
Solution: (a) The initial investment earned interest for April-June and July- September quarter i.e. for two quarters. In this case i = 6/4 = 1½ % = 0.015, n 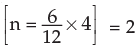
and the compounded amount = 800(1 + 0.015)2
= 800 × 1.03022500
= Rs. 824.18
The additional amount invested = Rs. (1000 - 824.18)
= Rs. 175.82
(b) In this case the time-deposit earned interest compounded monthly for six months.
Here i = 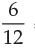 = 1/2 % = (0.005) n = 6 and P = Rs. 1000
= 1/2 % = (0.005) n = 6 and P = Rs. 1000
=  × 12Maturity value = 1000(1+0.005)6
× 12Maturity value = 1000(1+0.005)6
= 1000×1.03037751
= Rs. 1030.38
(c) Total interest earned = Rs. (24.18+30.38) = Rs. 54.56
FAQs on ICAI Notes: Time Value of Money- 1 - CA Foundation
| 1. What is the time value of money? |  |
| 2. What are the different types of interest rates used in time value of money calculations? |  |
| 3. How is the present value of a future cash flow calculated? |  |
| 4. What is the difference between annuity and perpetuity in time value of money? |  |
| 5. How does inflation affect time value of money calculations? |  |




















