Syllogism Tips and Tricks for Government Exams
| Table of contents |

|
| Syllogism Shortcuts |

|
| Case # All - Some |

|
| Case # Some - Some Not |

|
| Case # No- Some Not |

|
| Simple Case |

|
| ' Either Or ' & ' Neither Nor ' |

|
| Possibility |

|

Syllogism Shortcuts
I will start with explaining basic syllogism terminology which will be followed by practical examples.
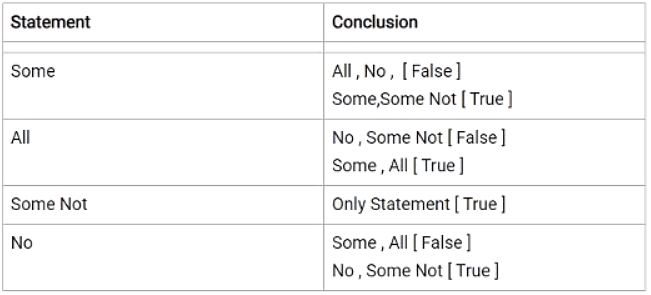
1. All
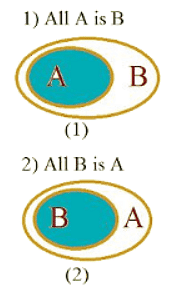
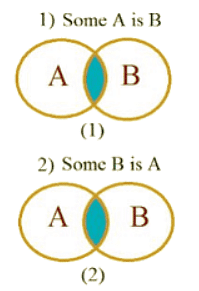
2. Some
3. NO
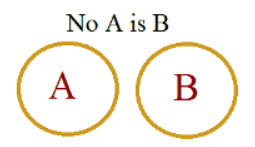
Case # All - Some

Let!
You have 1000 $ in your pocket.One of your friend needs 600 $ to pay his Bill.He wants to borrow money from you.He comes to you and say,"Do you have 600 $ ?.What would you say,"Afcoss Yes!".Even if He ask for 1 $, or 999 $ .Your answer will always "Yes!".
So Overall you had 1000 $ which is called "All " or All of the money you had & What is your friend want some of the money like here 600 or it could be 1$ or 999 $ and what we call that some portion of money out of it.or " Some".
That's why In " All " Case, "Some" is always true.
Example: Statement: All A are B.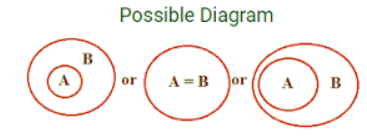
Conclusion
All A are B ✓
Some A are B ✓
Some B are A ✓
Some A are not B ✘
Some B are not A ✘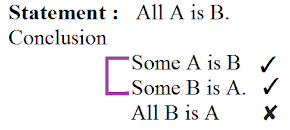
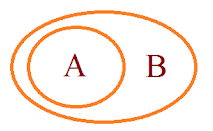
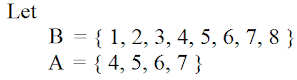
Now Here we can see that A contains set of numbers. So we call it is as Set A and Same for B 'Set B'.
All the numbers in A is contained by B hence All A is B true But All the numbers in B is not in A or not contain by A so All B is A → False.
Now Let understand How All A is B → True But All B is A → False
Let Box A & Box B. Here We can see that Box B is inside the Box A Hence Box B can fit into Box A but Box A cannot fit into Box B.
Case # Some - Some Not
 Assume you have given the exam & you passed with some marks that mean you got some marks and some or not. Even if you passed the exam with 99% marks still you missed the 1%. So Even 99% is count under the same case. and 1% is also counted in some case. hence In 'Some' case 'Some Not' is true.
Assume you have given the exam & you passed with some marks that mean you got some marks and some or not. Even if you passed the exam with 99% marks still you missed the 1%. So Even 99% is count under the same case. and 1% is also counted in some case. hence In 'Some' case 'Some Not' is true.
Statement: Some A are B
Conclusion
All B are A ✘
Some B are A ✓
No A is B ✘
Statement: Some A are not B

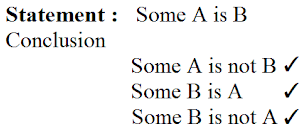
 Explanation:
Explanation: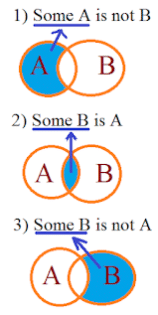
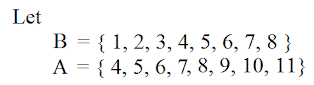
Here we see that Set A & Set B has some common values hence we can say that Some A is B & Some B is A But there also some values which are not common in both A & B. So We can also say that Some A are not B & Some B are not A.
Case # No- Some Not
 Assume You have no money in your pocket. So if you got no money. It means also that some money is not in your pocket. Having No means also some not.
Assume You have no money in your pocket. So if you got no money. It means also that some money is not in your pocket. Having No means also some not.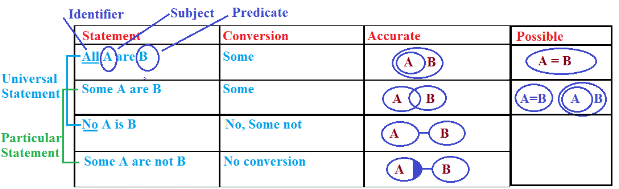
Point to Remember while Solving Syllogism
- Anything is possible in a statement.
like Some pens are fans. No fan is heater - Negative Answer will never be there.
Simple Case
Examples
Example 1: Statement: Some A are B, Some B are C , All C are D
Conclusion
Some A are not D ✘
Some B are D ✓
Some A are C ✘
Example 2: Statement: Some A are B, Some B are C, No C is D
Conclusion
Some B are not D ✘
Some D are not B ✘
Some A are C ✘
Example 3: Statement: All A are B , All A are C , All A are D , No D is E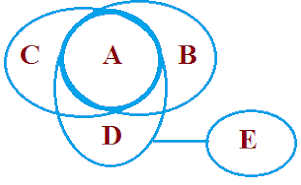
Conclusion:
Some B are not E ✓
Some A are not E ✓
No C is E ✓
No A is E ✓
No E is A ✓
Example 4: Statement: Some A are B, Some B are C, Some C are D, Some D are E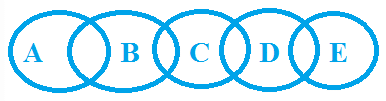
Conclusion
Some C are not A ✘
Some B are not D ✘
Some A are E ✘
All B are D ✘
No A is E ✘
Some C are A ✘
All B are E ✘
No B is E ✘
' Either Or ' & ' Neither Nor '
Complementary Pair
- If One Conclusion is positive & One is Negative
No - Some
Some - Some Not
All - Some Not - Same Subject & Same Predicate are there
- & not able to draw both the conclusion then answer will be Either Or
Examples
Example 1: Statement: All A are B, All A are C, All A are D, No D is E, Some F is C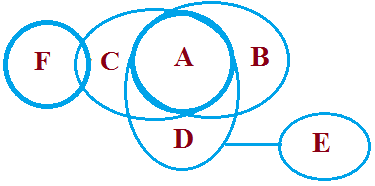 Conclusion
Conclusion
Example 2: Statement : Some A are B, Some B are C, Some C are D, Some D are E
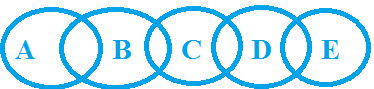 Conclusion
Conclusion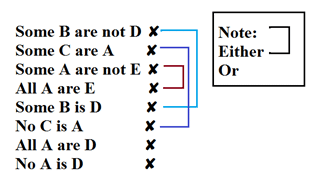
Exception
- In case of Universal (like 'All & No' ) Conclusion Complementary pair does not work
- In this type of Question " Neither Nor "
Example 3: Statement: Some A are B, All B are C, No C is D
Conclusion
Some A are not D ✘
No B is D ✘
Some A are C ✘
Some D are B ✘
Example 4: Statement: All A are B, No B is C, All C are D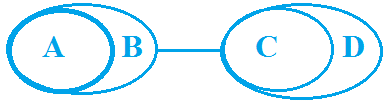
Conclusion
Some A are not D ✘
No D is B ✘
No A is C ✓
No A is D ✓
No D is A ✘
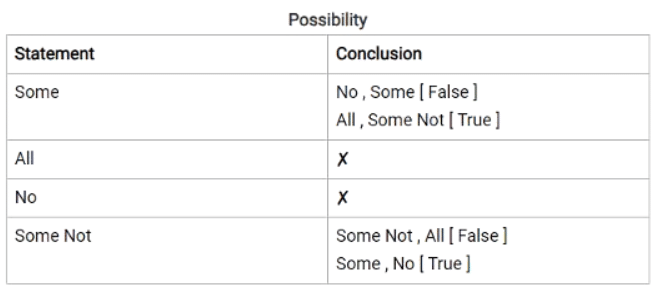
Possibility

Example
Example: Statement: Some A are B, Some B are C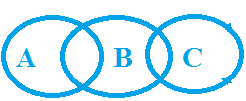 Conclusion
Conclusion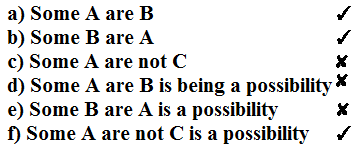
Explanation (Simple case A, B & C):
Let A, B & C are three person. A & B know each other. B & C know each other But B knows both. Now, Will A talk about C?
The answer is 'Not!, Neither Positive Nor Negative' because he doesn't know him. So conclusion C is False.
Possibility Case (Conclusion : D, E & F):
Now Let's take a look at conclusion E.Now Suppose there is raining outside your home and someone comes to you and say there is a possibility to rain today. What would you say to him,' Mad!"The Same scenario is here By looking at diagram it clearly says that Some B are A then how could say it is 'possible' which is actually there. Hence Possibility makes it wrong or false the conclusion. So Conclusion E is wrong.
Now talk about conclusion F which says Some A are not c which we don't know but it says to let it is a 'possibility' so anything could be possible which doesn't make our statement wrong or contradict with statement. If we make it like this below:
We talk here about possibility which could be anything which especially not contradict with our statement. So F which was False in Simple Case but When we talk about the possibility is becoming true.
Let's take another example for this. Now Let There is a cloudy sky outside your home. Someone comes to you and say," There is a possibility that there might be rain today", Now you have no idea whether it rain today or not. So you might be saying ," Bro! It is possible".Now here you cannot talk about negative because in Syllogism Negative Answer will never be there.
In a statement word like these called possibilities
- Can be
- Possible
- May be / might be
- Chances
- Occurs
- is being a possibility
- is a possible
In a statement word like these called sureties
- Can Never be
- Can
|
66 videos|253 docs
|
FAQs on Syllogism Tips and Tricks for Government Exams
| 1. What is syllogism in logic? |  |
| 2. How many types of syllogism are there? |  |
| 3. What is the major premise in a syllogism? |  |
| 4. Can you give an example of a syllogism? |  |
| 5. How can I improve my syllogism skills for exams? |  |




















