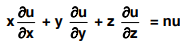Electrical Engineering (EE) Exam > Electrical Engineering (EE) Notes > Engineering Mathematics for Electrical Engineering > Total Derivative, Gradient, Divergence, and Curl
Total Derivative, Gradient, Divergence, and Curl | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) PDF Download
| Table of contents |
|
| Partial and Total Derivatives |
|
| Partial derivatives of higher order |
|
| Euler’s theorem on Homogenous functions |
|
| Composite functions |
|
Partial and Total Derivatives
Functions of two variablesIf three variables x, y, z are so related that the value of z depends upon the values of x and y, then z is called the function of two variables x and y and this is denoted by z = f(x, y)
Partial derivatives of first order
Let z = f(x, y) be a function of two independent variables x and y. If y is kept constant and x alone is allowed to vary then z becomes a function of x only. The derivative of z with respect to x, treating y as constant, is called partial derivative of z with respect to x and is denoted by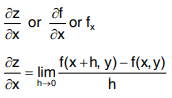
Similarly the derivative of z with respect to y, treating x as constant, is called partial derivative of z with respect to y and is denoted by
Thus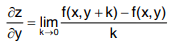 
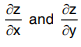are called first order partial derivatives of z
Partial derivatives of higher order
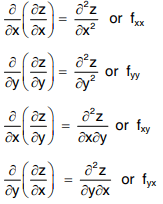
In general,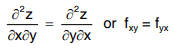 
Solved Examples 1: First order partial derivative of u = yx is
Solution : u = yx
Treating y as constant
treating x as constant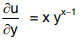
Euler’s theorem on Homogenous functions
If u is a homogenous function of degree n in x and y then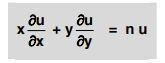
Since u is a homogenous function of degree n in x and y it can be expressed asu = xn f
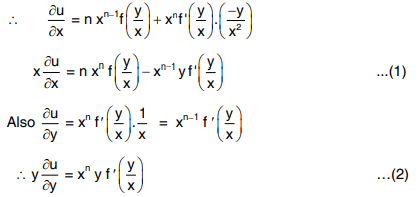
Adding (1) and (2) we get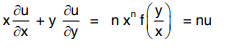
Note: Euler’s theorem can be extended to a homogenous function of any number of variables. Thus if u is a homogenous function of degree n in x, y and z then
Solved Examples 2: If 
show that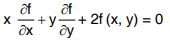 
.
Solution: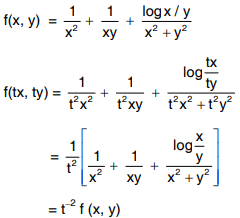 
f (x, y) is a homogenous function of degree -2 in x and y
By Euler’s theorem, we have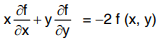
 |
Download the notes
Total Derivative, Gradient, Divergence, and Curl
|
Download as PDF |
Download as PDF
Composite functions
(i) If u = f (x, y) where x = ϕ(t), y = Ψ(t)then u is called a composite function of (the single variable) t and we can find du/dt .
(ii) If z = f(x, y) where x = ϕ(u, v), y = Ψ(u, v)
then z is called a composite function of (2 variables) u & v so that we can find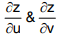 
Total derivative of composite functions
If u is a composite function of t, defined by the relations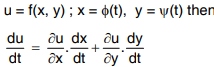
Solved Example 3: Find du/dt when u = x when u = xy2 + x2 y, x = at2, y = 2at.
Solution: The given equations define u as a composite function of t.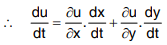
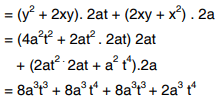
= 2a3 t3 (5t + 8)
Also u = xy2 + x2 y = at2 . 4a2 t2 + a2 t4 . 2at = 4a3 t4 + 2a3 t5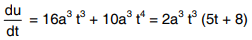 
The document Total Derivative, Gradient, Divergence, and Curl | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) is a part of the Electrical Engineering (EE) Course Engineering Mathematics for Electrical Engineering.
All you need of Electrical Engineering (EE) at this link: Electrical Engineering (EE)
|
44 videos|102 docs|58 tests
|
Related Exams
About this Document
4.71/5
Rating
Mar 29, 2025
Last updated
Document Description: Total Derivative, Gradient, Divergence, and Curl for Electrical Engineering (EE) 2025 is part of Engineering Mathematics for Electrical Engineering preparation.
The notes and questions for Total Derivative, Gradient, Divergence, and Curl have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about Total Derivative, Gradient, Divergence, and Curl covers topics
like Partial and Total Derivatives, Partial derivatives of higher order, Euler’s theorem on Homogenous functions, Composite functions and Total Derivative, Gradient, Divergence, and Curl Example, for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Total Derivative, Gradient, Divergence, and Curl.
Introduction of Total Derivative, Gradient, Divergence, and Curl in English is available as part of our Engineering Mathematics for Electrical Engineering
for Electrical Engineering (EE) & Total Derivative, Gradient, Divergence, and Curl in Hindi for Engineering Mathematics for Electrical Engineering course.
Download more important topics related with notes, lectures and mock test series for Electrical Engineering (EE)
Exam by signing up for free. Electrical Engineering (EE): Total Derivative, Gradient, Divergence, and Curl | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE)
Description
Full syllabus notes, lecture & questions for Total Derivative, Gradient, Divergence, and Curl | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) - Electrical Engineering (EE) | Plus excerises question with solution to help you revise complete syllabus for Engineering Mathematics for Electrical Engineering | Best notes, free PDF download
Information about Total Derivative, Gradient, Divergence, and Curl
In this doc you can find the meaning of Total Derivative, Gradient, Divergence, and Curl defined & explained in the simplest way possible. Besides explaining types of
Total Derivative, Gradient, Divergence, and Curl theory, EduRev gives you an ample number of questions to practice Total Derivative, Gradient, Divergence, and Curl tests, examples and also practice Electrical Engineering (EE)
tests
Related Searches
Important questions
,Viva Questions
,MCQs
,and Curl | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE)
,Previous Year Questions with Solutions
,Total Derivative
,Total Derivative
,Summary
,Sample Paper
,Exam
,and Curl | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE)
,and Curl | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE)
,Gradient
,Objective type Questions
,Gradient
,ppt
,past year papers
,Semester Notes
,Gradient
,Divergence
,Free
,Divergence
,study material
,shortcuts and tricks
,mock tests for examination
,video lectures
,Total Derivative
,Divergence
,practice quizzes
,Extra Questions
;
Additional Information about Total Derivative, Gradient, Divergence, and Curl for Electrical Engineering (EE) Preparation
Total Derivative, Gradient, Divergence, and Curl Free PDF Download
The Total Derivative, Gradient, Divergence, and Curl is an invaluable resource that delves deep into the core of the Electrical Engineering (EE) exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Total Derivative, Gradient, Divergence, and Curl now and kickstart your journey towards success in the Electrical Engineering (EE) exam.
Importance of Total Derivative, Gradient, Divergence, and Curl
The importance of Total Derivative, Gradient, Divergence, and Curl cannot be overstated, especially for Electrical Engineering (EE) aspirants.
This document holds the key to success in the Electrical Engineering (EE) exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Total Derivative, Gradient, Divergence, and Curl Notes
Total Derivative, Gradient, Divergence, and Curl Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Total Derivative, Gradient, Divergence, and Curl.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Total Derivative, Gradient, Divergence, and Curl Notes on EduRev are your ultimate resource for success.
Total Derivative, Gradient, Divergence, and Curl Electrical Engineering (EE) Questions
The "Total Derivative, Gradient, Divergence, and Curl Electrical Engineering (EE) Questions" guide is a valuable resource for all aspiring students preparing for the
Electrical Engineering (EE) exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Total Derivative, Gradient, Divergence, and Curl on the App
Students of Electrical Engineering (EE) can study Total Derivative, Gradient, Divergence, and Curl alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Total Derivative, Gradient, Divergence, and Curl,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Total Derivative, Gradient, Divergence, and Curl is prepared as per the latest Electrical Engineering (EE) syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup