Total Stress Parameters | Soil Mechanics - Civil Engineering (CE) PDF Download
Total Stress Parameters
UU Tests:

All Mohr circles for UU test plotted in terms of total stresses have the same diameter.
The failure envelope is a horizontal straight line and hence 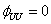
It can be represented by the equation:


For tests involving drainage in the first stage, when Mohr circles are plotted in terms of total stresses, the diameter increases with the confining pressure. The resulting failure envelope is an inclined line with an intercept on the vertical axis.
It is also observed that cCU ¹ cCD and fCU ¹ fCD
It can be stated that for identical soil samples tested under different triaxial conditions of UU, CU and CD tests, the failure envelope is not unique.
Effective Stress Parameters
If the same triaxial test results of UU, CU and CD tests are plotted in terms of effective stresses taking into consideration the measured pore water pressures, it is observed that all the Mohr circles at failure are tangent to the same failure envelope, indicating that shear strength is a unique function of the effective stress on the failure plane.

This failure envelope is the shear strength envelope which may then be written as

where c' = cohesion intercept in terms of effective stress
f' = angle of shearing resistance in terms of effective stress
If  is the effective stress acting on the rupture plane at failure,
is the effective stress acting on the rupture plane at failure, is the shear stress on the same plane and is therefore the shear strength.
is the shear stress on the same plane and is therefore the shear strength.
The relationship between the effective stresses on the failure plane is

Pore Water Pressure Parameters
The difference between the total and effective stresses is simply the pore water pressure u. Consequently, the total and effective stress Mohr circles have the same diameter and are only separated along the s - axis by the magnitude of the pore water pressure.
It is easy to construct a series of total stress Mohr Circles but the inferred total stress parameters have no relevance to actual soil behaviour. In principle, the effective strength parameters are necessary to check the stability against failure for any soil construction in the field. To do this, the pore water pressure in the ground under the changed loading conditions must be known and in general they are not.
In an undrained triaxial test with pore pressure measurement, this is possible and the effective stresses can then be determined. Alternatively, in drained tests, the loading rate can be made sufficiently slow so as to allow the dissipation of all excess pore water pressure. For low permeability soils, the drainage will require longer times.
In undrained tests, the general expression relating total pore water pressure developed and changes in applied stresses for both the stages is:
Du = Du1 + Du2 = B.Ds3+ B.A.(Ds1 - Ds3) = B[Ds3+ A(Ds1 - Ds3)]
where Du1 = pore water pressure developed in the first stage during application of confining stress Ds3,
Du2 = pore water pressure developed in the second stage during application of deviator stress (Ds1 - Ds3), and
B and A are Skempton's pore water pressure parameters.
Parameter B is a function of the degree of saturation of the soil (= 1 for saturated soils, and = 0 for dry soils). Parameter A is also not constant, and it varies with the over-consolidaton ratio of the soil and also with the magnitude of deviator stress. The value of A at failure is necessary in plotting the effective stress Mohr circles.
Consider the behaviour of saturated soil samples in undrained triaxial tests. In the first stage, increasing the cell pressure without allowing drainage has the effect of increasing the pore water pressure by the same amount.
Thus, there is no change in the effective stress. During the second shearing stage, the change in pore water pressure can be either positive or negative.
For UU tests on saturated soils, pore water pressure is not dissipated in both the stages (i.e., Du = Du1 + Du2).
For CU tests on saturated soils, pore water pressure is not dissipated in the second stage only (i.e., Du = Du2).
Stress-Strain Behaviour of Sands
Sands are usually sheared under drained conditions as they have relatively higher permeability. This behaviour can be investigated in direct shear or triaxial tests. The two most important parameters governing their behaviour are the relative density (ID) and the magnitude of the effective stress (s¢). The relative density is usually defined in percentage as

where emax and emin are the maximum and minimum void ratios that can be determined from standard tests in the laboratory, and e is the current void ratio. This expression can be re-written in terms of dry density as

where gdmax and gdmin are the maximum and minimum dry densities, and gd is the current dry density. Sand is generally referred to as dense if ID > 65% and loose if < 35%.
The influence of relative density on the behaviour of saturated sand can be seen from the plots of CD tests performed at the same effective confining stress. There would be no induced pore water pressures existing in the samples.


For the dense sand sample, the deviator stress reaches a peak at a low value of axial strain and then drops down, whereas for the loose sand sample, the deviator stress builds up gradually with axial strain. The behaviour of the medium sample is in between. The following observations can be made:
• All samples approach the same ultimate conditions of shear stress and void ratio, irrespective of the initial density. The denser sample attains higher peak angle of shearing resistance in between.
• Initially dense samples expand or dilate when sheared, and initially loose samples compress.
Worked Examples
Example 1: A UU test is carried out on a saturated normally consolidated clay sample at a confining pressure of
3 kg/cm2.The deviator stress at failure is 1 kg/cm2.
(a) Determine its total stress strength parameters.
(b) If another identical sample is tested at a confining pressure of 4 kg/cm2, what will be the vertical axial stress at failure?
Solution:

(a) 
From the plot, note that fUU = 0 and

(b)

UU tests on identical samples yield the same failure deviator stress 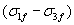 at all confining pressures.
at all confining pressures.
Therefore, the vertical axial stress at failure,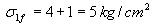
Example 2: Results of  tests conducted on two saturated clay samples are given. Determine the shear strength parameters.
tests conducted on two saturated clay samples are given. Determine the shear strength parameters.
Sample1 Sample2
Confining pressure ---------------- 4.8 kg/cm2 6.3 kg/cm2
Axial stress at failure -------------- 6.8 kg/cm2 9.3 kg/cm2
Pore water pressure at failure --- 3.8 kg/cm2 4.8 kg/cm2
Solution:

For sample 1:

For sample 2

From the plot, one can obtain

|
30 videos|76 docs|74 tests
|
FAQs on Total Stress Parameters - Soil Mechanics - Civil Engineering (CE)
| 1. What are the different stress parameters considered in civil engineering? |  |
| 2. How is axial stress calculated in civil engineering? |  |
| 3. What is shear stress and how is it determined in civil engineering? |  |
| 4. How is bending stress calculated for beams in civil engineering? |  |
| 5. What is bearing stress and how is it computed in civil engineering? |  |

|
Explore Courses for Civil Engineering (CE) exam
|

|

















