Transformation laws
Consider two sets of mutually orthogonal basis vectors which share a common origin. They correspond to a ‘new’ and an ‘old’ (original) Cartesian coordinate system which we assume to be right-handed characterized by two sets of basis vectors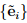 
and {ei}, respectively. Hence, the new coordinate system could be obtained from the original one by a rotation of the basis vectors ei about their origin. We then define the directional cosine matrix, Qij , as,
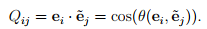(2.152)
Note that the first index on Qij indicates the ‘old’ components whereas the second index holds for the ‘new’ components.
It is worthwhile to mention that vectors and tensors themselves remain invariant upon a change of basis - they are said to be independent of the coordinate system. However, their respective components do depend upon the coordinate system introduced. This is the reason why a set of numbers arranged as a 3 by 1 or 3 by 3 matrix is not a vector or a tensor.
Vectorial transformation law
Consider some vector u represented using the two sets of basis vectors {ei} and 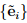, i.e.,
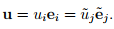(2.153)
Recalling the method to find the components of the vector along the basis directions, (2.15),
from the definition of the directional cosine matrix, (2.152). We assume that the relation between the basis vectors ei and 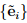is known and hence given the components of a vector in a basis, its components in another basis can be found using equation (2.154).
In an analogous manner, we find that
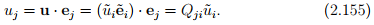
The results of equations (2.154) and (2.155) could be cast in matrix notation as
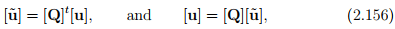
respectively. It is important to emphasize that the above equations are not identical to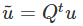 
and 
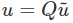respectively. In (2.156) [
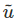] and [u] are column vectors characterizing components of the same vector in two different coordinate systems, whereas 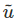and u are different vectors, in the later. Similarly, [Q] is a matrix of directional cosines, it is not a tensor even though it has the attributes of an orthogonal tensor as we will see next.
Combining equations (2.154) and (2.155), we obtain
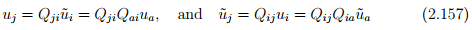
Hence,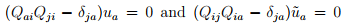 
for any vector u. Therefore,
Thus, the transformation matrix, Qij is sometimes called as orthogonal matrix but never as orthogonal tensor.
Tensorial transformation law
To determine the transformation laws for the Cartesian components of any second-order tensor A, we proceed along the lines similar to that done for vectors. Since, we seek the components of the same tensor in two different basis,
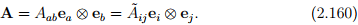
Then it follows from (2.46) that,
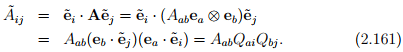
In matrix notation,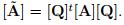 
In an analogous manner, we find that
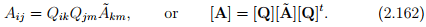
We emphasize again that these transformations relates the different matrices [à ] and [A], which have the components of the same tensor A and the equations [Ã] = [Q]t [A][Q] and [A] = [Q][à ][Q]t differ from the tensor equations à = QtAQ and A = QÃQt , relating two different tensors, namely A and à .
Finally, the 3n components Aj1j2...jn of a tensor of order n (with n indices j1, j2, . . ., jn) transform as
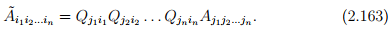
This tensorial transformation law relates the different components Ãi1i2...in (along the directions ê1, ê2, ê3) and Aj1j2...jn (along the directions e1, e2, e3) of the same tensor of order n. We note that, in general a second order tensor, A will be represented as Aijei⊗Ej , where {ei} and {Ej} are different basis vectors spanning the same space. It is not necessary that the directional cosines Qij = Ei · Êi and qij = ei ·êi be the same, where êi and Êj are the ‘new’ basis vectors with respect to which the matrix components of A is sought. Thus, generalizing the above is straightforward; each directional cosine matrices can be different, contrary to the assumption made.
Isotropic tensors
A tensor A is said to be isotropic if its components are the same under arbitrary rotations of the basis vectors. The requirement is deduced from equation (2.161) as
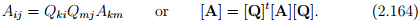
Of course here we assume that the components of the tensor are with respect to a single basis and not two or more independent basis.
Note that all scalars, zeroth order tensors are isotropic tensors. Also, zero tensors and unit tensors of all orders are isotropic. It can be easily verified that for second order tensors spherical tensor is also isotropic. The most general isotropic tensor of order four is of the form
where α, β, γ are scalars. The same in component form is given by: αδijδkl + βδikδjl + γδilδjk.
