Transformations - General Geometry | Additional Topics for IIT JAM Mathematics PDF Download
Common types of transformation
Any image in a plane could be altered by using different operations, or transformations. Here are the most common types: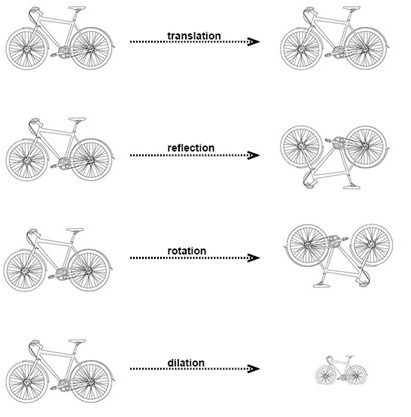
Translation is when we slide a figure in any direction.
Reflection is when we flip a figure over a line.
Rotation is when we rotate a figure a certain degree around a point.
Dilation is when we enlarge or reduce a figure.
Vectors
Vectors are used to represent a quantity that has both a magnitude and a direction. The vector is normally visualized in a graph. A vector between A and B is written as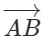
The vectors standard position has its starting point in origin.
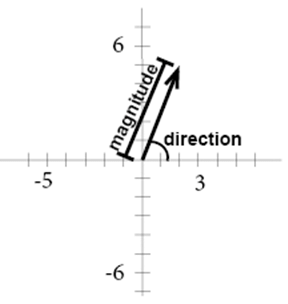
The component form of a vector is the ordered pair that describes the changes in the x- and y-values. In the graph above x1 = 0, y1 = 0 and x2 = 2, y2 = 5. The ordered pair that describes the changes is (x2 - x1, y2- y1), in our example (2-0, 5-0) or (2,5).
Two vectors are equal if they have the same magnitude and direction. They are parallel if they have the same or opposite direction.
We can combine vectors by adding them, the sum of two vectors is called the resultant.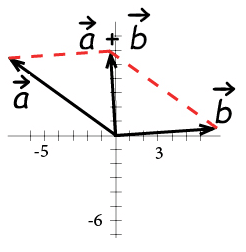
In order to add two vectors, we add the corresponding components.
Example
Add the two following vectors: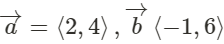
We add the corresponding components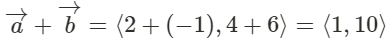
Transformation using matrices
A vector could be represented by an ordered pair (x,y) but it could also be represented by a column matrix:

Polygons could also be represented in matrix form, we simply place all of the coordinates of the vertices into one matrix. This is called a vertex matrix.
Example
A square has its vertexes in the following coordinates (1,1), (-1,1), (-1,-1) and (1,-1). If we want to create our vertex matrix we plug each ordered pair into each column of a 4 column matrix: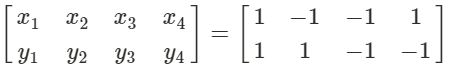
We can use matrices to translate our figure, if we want to translate the figure x+3 and y+2 we simply add 3 to each x-coordinate and 2 to each y-coordinate.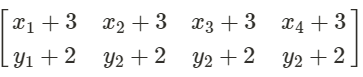
If we want to dilate a figure we simply multiply each x- and y-coordinate with the scale factor we want to dilate with.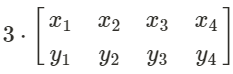
When we want to create a reflection image we multiply the vertex matrix of our figure with what is called a reflection matrix. The most common reflection matrices are:
for a reflection in the x-axis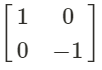
for a reflection in the y-axis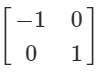
for a reflection in the origin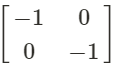
for a reflection in the line y = x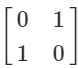
Example
We want to create a reflection of the vector in the x-axis.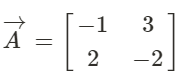
In order to create our reflection we must multiply it with correct reflection matrix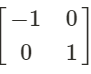
Hence the vertex matrix of our reflection is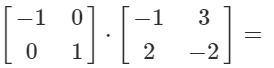
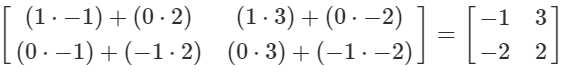
If we want to rotate a figure we operate similar to when we create a reflection. If we want to counterclockwise rotate a figure 90° we multiply the vertex matrix with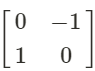
If we want to counterclockwise rotate a figure 180° we multiply the vertex matrix with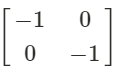
If we want to counterclockwise rotate a figure 270°, or clockwise rotate a figure 90°, we multiply the vertex matrix with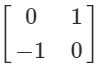
|
2 videos|45 docs|4 tests
|
















