Trigonometrical Ray Tracing | Additional Documents & Tests for IIT JAM PDF Download
No graphical construction can possibly be adequate to determine the aberration residual of a corrected lens, and for this an accurate trigonometrical computation must be made and carried out to six or seven decimal places, the angles being determined to single seconds of arc or less. There are many procedures for calculating the path of a ray through a system of spherical refracting or reflecting surfaces, the following being typical: The diagram in Figure represents a ray lying in the meridian plane, defined as the plane containing the lens axis and the object point. A ray in this plane is defined by its slope angle, U, and by the length of the perpendicular, Q, drawn from the vertex (A) of the surface on to the ray. By drawing a line parallel to the incident ray through the centre of curvature C, to divide Q into two parts at N, the relation is stated as AN = r sin U, and NM = r sin I. Hence

Figure: Trigonometrical ray tracing (see text).
Q = r(sin U + sin I) (2)
From this the first ray-tracing equation can be derived,
 (3a)
(3a)
Applying the law of refraction, equation (2), gives the second equation
Q = r(sin U + sin I) (2)
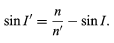 (3b)
(3b)
Because the angle PCA = U + I = U′ + I′, the slope of the refracted ray can be written as
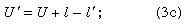
and, lastly, by adding primes to equation (2),
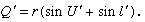
in which d is the axial distance from the first to the second refracting surface. After performing this calculation for all the surfaces in succession, the longitudinal distance from the last surface to the intersection point of the emergent ray with the lens axis is found by
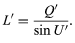
Corresponding but much more complicated formulas are available for tracing a skew ray, that is, a ray that does not lie in the meridian plane but travels at an angle to it. After refraction at a surface, a skew ray intersects the meridian plane again at what is called the diapoint. By tracing the paths of a great many (100 or more) meridional and skew rays through a lens, with the help of an electronic computer, and plotting the assemblage of points at which all these rays pierce the focal plane after emerging from the lens, a close approximation to the appearance of a star image can be constructed, and a good idea of the expected performance of a lens can be obtained.

|
Explore Courses for IIT JAM exam
|

|

















