Simple Pendulum | Physics for JEE Main & Advanced PDF Download
Simple Pendulum
A simple pendulum consists of a heavy point mass suspended from a rigid support by means of an elastic inextensible string.
The time period of the simple pendulum is given by :
T = 2π √l / g
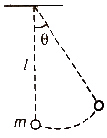
where l = effective length of the pendulum and g = acceleration due to gravity.
If the effective length l of simple pendulum is very large and comparable with the radius of earth (R), then its time period is given by
T = 2π √Rl / (l + R)g
For a simple pendulum of infinite length (l >> R)
T = 2π √R / g = 84.6 min
For a simple pendulum of length equal to radius of earth,
T = 2π √R / g = 60 min
If the bob of the simple pendulum is suspended by a metallic wire of length l, having coefficient of linear expansion α, then due to increase in temperature by dθ, then
Effective length l’ = l (1 + α dθ)
Percentage increase in time period
(T’ / T – 1) * 100 = 50 α dθ
When a bob of simple pendulum of density ρ oscillates in a fluid of density ρo (ρo < p), then time period get increased.
Increased time period T’ = T √ρ / ρ – ρo
When simple pendulum is in a horizontally accelerated vehicle, then its time period is given by
T = 2π √1 / √(a2 + g2)
where a = horizontal acceleration of the vehicle.
When simple pendulum is in a vehicle sliding down an inclined plane, then its time period is given by
T = 2π √l / g cos θ
Where θ = inclination of plane.
Second’s Pendulum
A simple pendulum having time period of 2 second is called second’s Pendulum.
The effective length of a second’s pendulum is 99.992 em of approximately 1 metre on earth.
Conical Pendulum
If a simple pendulum is fixed at one end and the bob is rotating in a horizontal circle, then it is called a conical pendulum.
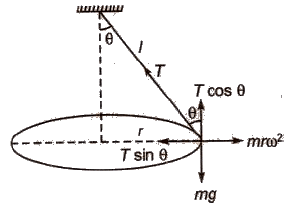
In equilibrium T sin θ = mrΩ2
Its time period T = 2π √mr / T sin θ
Compound Pendulum
Any rigid body mounted, so that it is capable of swinging in a vertical plane about some axis passing through it is called a physical or compound pendulum.
Its time period is given by
T = 2π √l / mg l
where, I = moment of inertia of the body about an axis passing through the centre of suspension,
m = mass of the body and
l = distance of centre of gravity from the centre of suspension.
Torsional Pendulum
Time period of torsional pendulum is given by
T = 2π √I / C

where, I = moment of inertia of the body about the axis of rotation and
C = restoring couple per unit twist.
Physical Pendulum
When a rigid body of any shape is capable of oscillating about an axis (mayor may not be passing through it). it constitutes a physical pendulum.
T = 2π √I / mgd

- The simple pendulum whose time period is same as that of a physical pendulum is termed as an equivalent simple pendulum.
T = 2π √I / mgd = 2 π √l / g
- The length of an equivalent simple pendulum is given by l = I / md
Spring Pendulum
A point mass suspended from a massless (or light) spring constitutes a spring pendulum. If the mass is once pulled downwards so as to stretch the spring and then released. the system oscillated up and down about its mean position simple harmonically. Time period and frequency of oscillations are given by
T = 2π √m / k or v = 1 / 2π √k / m

If the spring is not light but has a definite mass ms, then it can be easily shown that period of oscillation will be
T = 2π √(m + ms / 3) / k
|
289 videos|635 docs|179 tests
|
FAQs on Simple Pendulum - Physics for JEE Main & Advanced
| 1. What is a simple pendulum? |  |
| 2. How does the period of a simple pendulum depend on its length? |  |
| 3. What factors affect the period of a simple pendulum? |  |
| 4. How can the period of a simple pendulum be calculated? |  |
| 5. What are some real-life applications of simple pendulums? |  |

|
Explore Courses for JEE exam
|

|


















