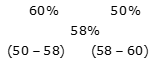Important Concepts: Mixtures & Alligations | Quantitative Aptitude (Quant) - CAT PDF Download
| Table of contents |

|
| Meaning: Mixtures & Alligations |

|
| Types of Mixtures |

|
| Rule of Alligation |

|
| Important Formulae |

|
| Applications of Alligations |

|
Meaning: Mixtures & Alligations
- Mixing things together is called a mixture.
- Alligation helps us figure out how much of each thing is mixed together and at what price they are sold to make a profit or suffer a loss.

- To solve mixture and alligation problems, you need to understand that alligation helps find the average value of a mixture when the ratio and quantity of the ingredients mixed are different. It also helps figure out the proportion in which the elements are mixed.

Types of Mixtures
- Simple Mixtures:- When two or more different ingredients are mixed together, a simple mixture is formed. The sums based on simple mixtures are pretty straightforward and easy to solve.
For example, alloys are mixtures of two or more metals. Alloys are simple mixtures. - Compound Mixtures:- When two or more simple mixtures are mixed together, a compound mixture is formed. Hence, more ratios need to be calculated while solving the sum of complex mixtures.
For example, when two metal alloys made from a combination of different elements are mixed together, then it leads to the formation of a complex mixture.
Rule of Alligation
The rule enables us to find the ratio in which two or more ingredients/mixture of different prices/concentration are mixed together to form a final mixture or desired price or concentration.
Two methods are used:
Method 1 (Formula Method):
It is given as- 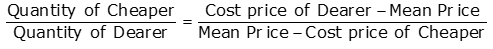
Method 2 (Diagram Method):
The above method can be expressed using a diagram which will be more convenient to understand-
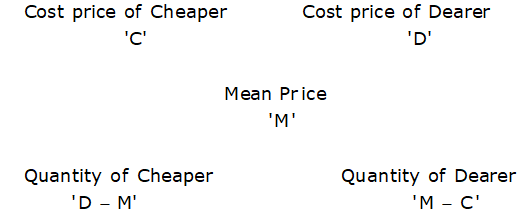
Note:
This rule of allegation can be applied to other topics such as profit and loss, average, percentage, simple interest/compound interest, ratio, and proportion.
Example: 30 boys with an average weight of 60 kgs and 20 girls with an average weight of 40. Find the average weight of the whole class? Find the average weight of the whole class?
Solution: To find the answer to the above question, one can use the formula for weighted average. Suppose the question was framed a bit differently, the Average weight of boys is 60, the average weight of girls is 40 and average weight of the whole class is 52.
Find the ratio between the number of boys and girls
Solution: The fastest way to solve this question would be by using Alligation. Read below for its solution using alligation.
So what exactly is Alligation?
It is the reverse of weighted average; i.e. if the averages of two groups are separately given and the average of the whole group is given, then we can find out the ratio between the groups.
For example, in the above question, the data given is-
Average weight of boys = 60, average weight of girls = 40 and average weight of the whole class is = 52
The data can be represented in an Alligation chart as given below and use it to find the ratio between the number of boys and girls in the class.

Take the difference across: x = 60-52 = 8 and y = 52-40 = 12. That is how we get the ratio between the boys and girls as 12:8 or 3:2.Let us look at another question where you can use
Let’s look at another question where you can use Alligation.
Example: In what ratio should a shopkeeper mix two types of rice, one costing 20 rupees/kg and another costing 10 rupees/kg to get a rice variety costing 14 rupees/kg?
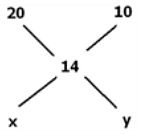
Sol: Here also we can use Alligation as follows:
x = 14-10 = 4 y = 20-14 = 6 The ratio between the type 1 and type 2 rice is 4:6 or 2:3
Important Formulae
To solve math problems, you should learn specific formulas for each topic. These formulas make solving questions quicker and easier. Here are some formulas that will help you solve mixture and alligation problems more easily.
The basic formula which is used to find the ratio in which the ingredients are mixed is:
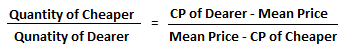
It is also called the rule of alligation and can also be represented as
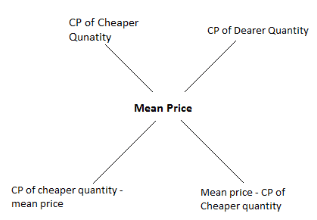
Applications of Alligations
Alligation in Mixture Problems
We will see how the rule of allegation can be applied in mixture problems-
Example 1: A shopkeeper mixes 30 kg of type A rice of Rs.40/kg and 45 kg of type B rice of Rs.30/kg, then find the price of formed mixture of rice.
Sol:
By the rule of alligation:
(30 – M): (M – 40) = 30: 45 = 2: 3
90 – 3M = 2M – 805M = 170M = 34
Hence, price of mixture = Rs.34/kg
Note: After applying the concept of alligation on the price of the item of concentration of mixture we will get the ratio in which these two items or mixture are mixed.
Sol: Water percent in mixture A = 100% – 75% of 25%
By the rule of alligation:Required ratio = -5: -10
= 1: 2
Alligation in Profit and Loss Problems
Example 3: A shopkeeper sells type A rice at 20% profit and type B rice at 15% loss. If overall he earns 13% profit, then find the cost price of type A rice to type B rice.
Sol: By the rule of alligation:
The ratio of the cost price of type A to type B rice = -28: -7
= 4: 1
Note: After applying alligatiion concept in profit/loss percent earned on the items we will get the ratio of cost prices of the items.

Example 4: A shopkeeper purchased a table for Rs.1200 and sold it at 20% profit, he purchased a chair at Rs.400 and sold it at 10% profit, the find the overall profit percent earned by him.
Sol: Let overall profit percent = M%
By the rule of allegation:
(10 – M): (M – 20) = 1200: 400 = 3: 1
10 – M = 3M – 60
4M = 70
M = 17.5
Hence, overall profit percent = M = 17.5%
Alligation in Speed, distance, and Time Problems
The concept of mixture and alligation can be used to find the average speed of journey.
Example 5: A person covers the first 3 hours of a journey with a speed 80 km/h and the remaining 5 hours with a speed 56 km/h, then find his average speed of the journey.
Sol: Let average speed = X
By the rule of allegation:
(56 – X): (X – 80) = 3: 5
280 – 5X = 3X – 240
8X = 520
X = 65
Average speed of journey = 65 km/h
Note: After applying the concept of alligation on speed on different parts of the journey we will get the ratio of time taken to cover those parts.
Example 6: A distance of 360 km can be covered in 6 hours when some part of the journey is covered with speed 45 km/h and remaining with speed 90 km/h, then find the distance covered with speed 45 km/h.
Sol: Average speed of the journey = 360/6 = 60 km/h
By the rule of allegation:
Ratio of time taken = 30: 15 = 2: 1
Time for which journey is covered with speed 45 km/h = 6 * (2/3) = 4 hours
Distance covered by 45 km/h speed = 45 * 4 = 180 km
Alligation in Simple/Compound Interest Problems
The concept of alligation can be applied to SI and CI if we can calculate the effective interest rate for given time period.
For example:
Equivalent of 20% SI for 3 years = 20% * 3 = 60%
Equivalent of 20% CI for 2 years = [(1.2)2 – 1] * 100 = 44%
Example 7: Rahul lent Rs.5000 to Sumit at 25% SI for 2 years and borrowed Rs.3000 from Suresh for 3 years 10% SI, then find the profit/loss on interest amount of Rahul.
Sol: Effective rate of interest for 2 years on lent amount = 25% * 2 = 50%
Effective rate of interest for 3 years on borrowed amount = -10% * 3 = -30% [Negative because interest will be given.]
By the rule of allegation:
(-30 – X): (X – 50) = 5000: 3000 = 5: 3
-90 – 3X = 5X – 250
8X = 160
X = 20
Hence, total profit on interest amount = 20% of (5000 + 3000) =
= Rs.1600
Note: After applying the alligation concept in effective interest rate we will get the ratio of amount invested.
Alligation in Average, Ratio, and Percentage Problems
By applying the rule of alligation we can solve the problems of averages, ratios, and percentages quickly.
Example 8: Average age of a 25 students of a class is 24 years and average age of remaining 15 students of the class is 18 years, then find the average age of the class.
Sol: Let average age of class = A
By the rule of alligation:
(18 – A): (A – 24) = 25: 15 = 5: 3
54 – 3A = 5A – 120
8A = 174
A = 21.75
Hence, average age of the class = A = 21.75 years
Example 9: Ratio of marks obtained to maximum marks by Arun in math and English is 5: 3 and 3: 1. If maximum marks in both the subjects are same, then find the ratio of marks obtained to maximum marks by Arun when both the subjects are taken together.
Sol: By the rule of alligation:
(3/4 – A): (A – 5/8) = 1: 1
3/4 – A = A – 5/8
2A = 11/8
A = 11/16
Required ratio = 11: (16 – 11) = 11: 5
Example 10: In states A and B out of the total population, the male population is 60% and 50% respectively. If the male population, when both the states are taken together, becomes 58% of the total population, then find that total population of state B is what percent of that of state A.
Sol: By the rule of allegation:
Ratio of total population of state A to that of state B = -8: -2 = 4: 1
Required percent = (1/4) * 100
= 25%
|
191 videos|131 docs|110 tests
|
FAQs on Important Concepts: Mixtures & Alligations - Quantitative Aptitude (Quant) - CAT
| 1. What is the concept of mixtures and alligations in mathematics? |  |
| 2. What are the different types of mixtures? |  |
| 3. How do you apply the rule of alligation? |  |
| 4. What are some important formulae used in mixtures and alligations? |  |
| 5. What are the applications of alligations in real life? |  |

|
Explore Courses for CAT exam
|

|