ICAI Notes- Unit I: Index Numbers- 1 | Quantitative Aptitude for CA Foundation PDF Download

19.1.1 INTRODUCTION:- Index numbers are convenient devices for measuring relative changes of differences from time to time or from place to place. Just as the arithmetic mean is used to represent a set of values, an index number is used to represent a set of values over two or more different periods or localities.
The basic device used in all methods of index number construction is to average the relative change in either quantities or prices since relatives are comparable and can be added even though the data from which they were derived cannot themselves be added. For example, if wheat production has gone up to 110% of the previous year’s producton and cotton production has gone up to 105%, it is possible to average the two percentages as they have gone up by 107.5%. This assumes that both have equal weight; but if wheat production is twice as important as cotton, percentage should be weighted 2 and 1. The average relatives obtained through this process are called the index numbers.
Definition: An index number is a ratio of two or more time periods are involved, one of which is the base time period. The value at the base time period serves as the standard point of comparison.
Example: NSE, BSE, WPI, CPI etc.
An index time series is a list of index numbers for two or more periods of time, where each index number employs the same base year.
Relatives are derived because absolute numbers measured in some appropriate unit, are often of little importance and meaningless in themselves. If the meaning of a relative figure remains ambiguous, it is necessary to know the absolute as well as the relative number.
Our discussion of index numbers is confined to various types of index numbers, their uses, the mathematical tests and the principles involved in the construction of index numbers.
Index numbers are studied here because some techniques for making forecasts or inferences about the figures are applied in terms of index number. In regression analysis, either the independent or dependent variable or both may be in the form of index numbers. They are less unwieldy than large numbers and are readily understandable.
These are of two broad types: simple and composite. The simple index is computed for one variable whereas the composite is calculated from two or more variables. Most index numbers are composite in nature.
19.1.2 ISSUES INVOLVED:- Following are some of the important criteria/problems which have to be faced in the construction of index Numbers.
Selection of data: It is important to understand the purpose for which the index is used. If it is used for purposes of knowing the cost of living, there is no need of including the prices of capital goods which do not directly influence the living.
Index numbers are often constructed from the sample. It is necessary to ensure that it is representative. Random sampling, and if need be, a stratified random sampling can ensure this.
It is also necessary to ensure comparability of data. This can be ensured by consistency in the method of selection of the units for compilation of index numbers.
However, difficulties arise in the selection of commodities because the relative importance of commodities keep on changing with the advancement of the society. More so, if the period is quite long, these changes are quite significant both in the basket of production and the uses made by people.
Base Period: It should be carefully selected because it is a point of reference in comparing various data describing individual behaviour. The period should be normal i.e., one of the relative stability, not affected by extraordinary events like war, famine, etc. It should be relatively recent because we are more concerned with the changes with reference to the present and not with the distant past. There are three variants of the base fixed, chain, and the average.
Selection of Weights: It is necessary to point out that each variable involved in composite index should have a reasonable influence on the index, i.e., due consideration should be given to the relative importance of each variable which relates to the purpose for which the index is to be used. For example, in the computation of cost of living index, sugar cannot be given the same importance as the cereals.
Use of Averages: Since we have to arrive at a single index number summarising a large amount of information, it is easy to realise that average plays an important role in computing index numbers. The geometric mean is better in averaging relatives, but for most of the indices arithmetic mean is used because of its simplicity.
Choice of Variables: Index numbers are constructed with regard to price or quantity or any other measure. We have to decide about the unit. For example, in price index numbers it is necessary to decide whether to have wholesale or the retail prices. The choice would depend on the purpose. Further, it is necessary to decide about the period to which such prices will be related. There may be an average of price for certain time-period or the end of the period. The former is normally preferred.
Selection of Formula: The question of selection of an appropriate formula arises, since different types of indices give different values when applied to the same data. We will see different types of indices to be used for construction succeedingly.
19.1.3 CONSTRUCTION OF INDEX NUMBER:- Notations: It is customary to let  denote the prices during nth period for the first, second and third commodity. The corresponding price during a base period are denoted by
denote the prices during nth period for the first, second and third commodity. The corresponding price during a base period are denoted by  , etc. With these notations the price of commodity j during period n can be indicated by Pn(j). We can use the summation notation by summing over the superscripts j as follows:
, etc. With these notations the price of commodity j during period n can be indicated by Pn(j). We can use the summation notation by summing over the superscripts j as follows:
We can omit the superscript altogether and write as ∑Pn etc.
Relatives: One of the simplest examples of an index number is a price relative, which is the ratio of the price of single commodity in a given period to its price in another period called the base period or the reference period. It can be indicated as follows:
It has to be expressed as a percentage, it is multiplied by 100
There can be other relatives such as of quantities, volume of consumption, exports, etc. The relatives in that case will be:
Similarly, there are value relatives:
When successive prices or quantities are taken, the relatives are called the link relative,
When the above relatives are in respect to a fixed base period these are also called the chain relatives with respect to this base or the relatives chained to the fixed base. They are in the form of :
Methods: We can state the broad heads as follows:
19.1.3.1 SIMPLE AGGREGATIVE METHOD:- In this method of computing a price index, we express the total of commodity prices in a given year as a percentage of total commodity price in the base year. In symbols, we have
Simple aggregative price index = 
where ∑Pn is the sum of all commodity prices in the current year and ∑Po is the sum of all commodity prices in the base year.
ILLUSTRATIONS:-
Simple Aggregative Index for 1999 over 1998 
and for 2000 over 1998 
The above method is easy to understand but it has a serious defect. It shows that the first commodity exerts greater influence than the other two because the price of the first commodity is higher than that of the other two. Further, if units are changed then the Index numbers will also change. Students should independently calculate the Index number taking the price of eggs per dozen i.e., ₹36, ₹43.20, ₹39.60 for the three years respectively. This is the major flaw in using absolute quantities and not the relatives. Such price quotations become the concealed weights which have no logical significance.
19.1.3.2 SIMPLE AVERAGE OF RELATIVES:- One way to rectify the drawbacks of a simple aggregative index is to construct a simple average of relatives. Under it we invert the actual price for each variable into percentage of the base period. These percentages are called relatives because they are relative to the value for the base period. The index number is the average of all such relatives. One big advantage of price relatives is that they are pure numbers. Price index number computed from relatives will remain the same regardless of the units by which the prices are quoted. This method thus meets criterion of unit test (discussed later). Also quantity index can be constructed for a group of variables that are expressed in divergent units.
ILLUSTRATIONS:- In the proceeding example we will calculate relatives as follows:
Inspite of some improvement, the above method has a flaw that it gives equal importance to each of the relatives. This amounts to giving undue weight to a commodity which is used in a small quantity because the relatives which have no regard to the absolute quantity will give weight more than what is due from the quantity used. This defect can be remedied by the introduction of an appropriate weighing system.
19.1.3.3 WEIGHTED METHOD:- To meet the weakness of the simple or unweighted methods, we weigh the price of each commodity by a suitable factor often taken as the quantity or the volume of the commodity sold during the base year or some typical year. These indices can be classified into broad groups:
(i) Weighted Aggregative Index.
(ii) Weighted Average of Relatives.
(i) Weighted Aggregative Index: Under this method we weigh the price of each commodity by a suitable factor often taken as the quantity or value weight sold during the base year or the given year or an average of some years. The choice of one or the other will depend on the importance we want to give to a period besides the quantity used. The indices are usually calculated in percentages. The various alternatives formulae in use are:
(The example has been given after the tests).
(a ) Laspeyres’ Index: In this Index base year quantities are used as weights:
(b) Paasche’s Index: In this Index current year quantities are used as weights:
(c) Methods based on some typical Period:
Index  the subscript t stands for some typical period of years, the quantities of
the subscript t stands for some typical period of years, the quantities of
which are used as weight
Note: * Indices are usually calculated as percentages using the given formulae
The Marshall-Edgeworth index uses this method by taking the average of the base year and the current year
Marshall-Edgeworth Index = 
(d) Fisher’s ideal Price Index: This index is the geometric mean of Laspeyres’ and Paasche’s.
Fisher's Index = 
(ii) Weighted Average of Relative Method: To overcome the disadvantage of a simple average of relative method, we can use weighted average of relative method. Generally weighted arithmetic mean is used although the weighted geometric mean can also be used. The weighted arithmetic mean of price relatives using base year value weights is represented by
Example:-
Weighted Price Relative
19.1.3.4 THE CHAIN INDEX NUMBERS:-
So far we concentrated on a fixed base but it does not suit when conditions change quite fast.
In such a case the changing base for example, 1998 for 1999, and 1999 for 2000, and so on, may be more suitable. If, however, it is desired to associate these relatives to a common base the results may be chained. Thus, under this method the relatives of each year are first related to the preceding year called the link relatives and then they are chained together by successive multiplication to form a chain index.
The formula is:
Example:- The following are the index numbers by a chain base method: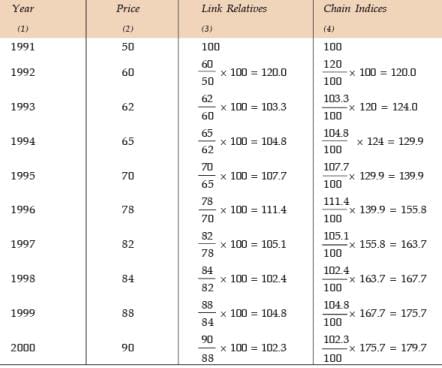
You will notice that link relatives reveal annual changes with reference to the previous year. But when they are chained, they change over to a fixed base from which they are chained, which in the above example is the year 1991. The chain index is an unnecessary complication unless of course where data for the whole period are not available or where commodity basket or the weights have to be changed. The link relatives of the current year and chain index from a given base will give also a fixed base index with the given base year as shown in the column 4 above.
19.1.3.5 QUANTITY INDEX NUMBERS:- To measure and compare prices, we use price index numbers. When we want to measure and compare quantities, we resort to Quantity Index Numbers. Though price indices are widely used to measure the economic strength, Quantity indices are used as indicators of the level of output in economy. To construct Quantity indices, we measure changes in quantities and weight them using prices or values as weights. The various types of Quantity indices are:
1 . Simple aggregate of quantities:
This has the formula 
2 . The simple average of quantity relatives:
This can be expressed by the formula 
3 . Weighted aggregate Quantity indices:
(i) With base year weight : 
(ii) With current year weight 
(iii) Geometric mean of (i) and (ii) : 
4 . Base-year weighted average of quantity relatives. This has the formula 
Note : Indices are usually calculated as percentages using the given formulae.
19.1.3.6 VALUE INDICES:-
Value equals price multiplied by quantity. Thus a value index equals the total sum of the values of a given year divided by the sum of the values of the base year, i.e.,
19.1.4 USEFULNESS OF INDEX NUMBERS:-
So far we have studied various types of index numbers. However, they have certain limitations.
They are :
1 . As the indices are constructed mostly from deliberate samples, chances of errors creeping in cannot be always avoided.
2 . Since index numbers are based on some selected items, they simply depict the broad trend and not the real picture.
3 . Since many methods are employed for constructing index numbers, the result gives different values and this at times create confusion.
In spite of its limitations, index numbers are useful in the following areas :
1 . Framing suitable policies in economics and business. They provide guidelines to make decisions in measuring intelligence quotients, research etc.
2 . They reveal trends and tendencies in making important conclusions in cyclical forces, irregular forces, etc.
3 . They are important in forecasting future economic activity. They are used in time series analysis to study long-term trend, seasonal variations and cyclical developments.
4 . Index numbers are very useful in deflating i.e., they are used to adjust the original data for price changes and thus transform nominal wages into real wages.
5 . Cost of living index numbers measure changes in the cost of living over a given period.
19.1.5 DEFLATING TIME SERIES USING INDEX NUMBERS:- Sometimes a price index is used to measure the real values in economic time series data expressed in monetary units. For example, GNP initially is calculated in current price so that the effect of price changes over a period of time gets reflected in the data collected. Thereafter, to determine how much the physical goods and services have grown over time, the effect of changes in price over different values of GNP is excluded. The real economic growth in terms of constant prices of the base year therefore is determined by deflating GNP values using price index.

19.1.6 SHIFTING AND SPLICING OF INDEX NUMBERS:- These refer to two technical points: (i) how the base period of the index may be shifted, (ii) how two index covering different bases may be combined into single series by splicing.
The formula used is,
Splicing two sets of price index numbers covering different periods of time is usually required when there is a major change in quantity weights. It may also be necessary on account of a new method of calculation or the inclusion of new commodity in the index.
You will notice that the old series upto 1994 has to be converted shifting to the base. 1995 i.e, 114.2 to have a continuous series, even when the two parts have different weights
19.1.7 TEST OF ADEQUACY:-
There are four tests:
(i) Unit Test: This test requires that the formula should be independent of the unit in which or for which prices and quantities are quoted. Except for the simple (unweighted) aggregative index all other formulae satisfy this test.
(ii) Time Reversal Test: It is a test to determine whether a given method will work both ways in time, forward and backward. The test provides that the formula for calculating the index number should be such that two ratios, the current on the base and the base on the current should multiply into unity. In other words, the two indices should be reciprocals of each other. Symbolically,
where P01 is the index for time 1 on 0 and P10 is the index for time 0 on 1.
You will notice that Laspeyres’ method and Paasche’s method do not satisfy this test, but Fisher’s Ideal Formula does.
While selecting an appropriate index formula, the Time Reversal Test and the Factor Reversal test are considered necessary in testing the consistency.
Laspeyres:
Paasche’s:
Fisher’s:
(iii) Factor Reversal Test: This holds when the product of price index and the quantity index should be equal to the corresponding value index, i.e., 
Symbolically: 
Fishers’


Thus Fisher’s Index satisfies Factor Reversal test. Because Fisher’s Index number satisfies both the tests in (ii) and (iii), it is called an Ideal Index Number.
(iv) Circular Test: It is concerned with the measurement of price changes over a period of years, when it is desirable to shift the base. For example, if the 1970 index with base 1965 is 200 and 1965 index with base 1960 is 150, the index 1970 on base 1960 will be 300. This property therefore enables us to adjust the index values from period to period without referring each time to the original base. The test of this shiftability of base is called the circular test.
This test is not met by Laspeyres, or Paasche’s or the Fisher’s ideal index. The simple geometric mean of price relatives and the weighted aggregative with fixed weights meet this test.
Example: Compute Fisher’s Ideal Index from the following data:
Show how it satisfies the time and factor reversal tests.
Solution:-
Fisher’s Ideal Index:

Time Reversal Test:
∴ Time Reversal Test is satisfied.
Factor Reversal Test:
 the Factor Reversal Test is satisfied.
the Factor Reversal Test is satisfied.
|
148 videos|174 docs|99 tests
|
FAQs on ICAI Notes- Unit I: Index Numbers- 1 - Quantitative Aptitude for CA Foundation
| 1. What is the purpose of using index numbers in accounting? |  |
| 2. How are index numbers calculated? |  |
| 3. What are the different types of index numbers? |  |
| 4. How are index numbers useful in financial analysis? |  |
| 5. What are the limitations of index numbers? |  |
|
148 videos|174 docs|99 tests
|

|
Explore Courses for CA Foundation exam
|

|


















