Class 8 Exam > Class 8 Notes > Mathematics Class 8- New NCERT (Ganita Prakash) > Unit Test: Quadrilaterals
Unit Test: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
Time: 1 hour
M.M. 30
Attempt all questions.
- Question numbers 1 to 5 carry 1 mark each.
- Question numbers 6 to 8 carry 2 marks each.
- Question numbers 9 to 11 carry 3 marks each.
- Question number 12 & 13 carry 5 marks each
Q1: The quadrilateral whose all its sides are equal and angles are equal to 90 degrees, it is called: (1 Mark)
a. Rectangle
b. Square
c. Kite
d. Parallelogram
Q2: The sum of all the angles of a quadrilateral is equal to: (1 Mark)
a. 180°
b. 270°
c. 360°
d. 90°
Q3: A trapezium has: (1 Mark)
a. One pair of opposite sides parallel
b. Two pairs of opposite sides parallel to each other
c. All its sides are equal
d. All angles are equal
Q4: A rhombus can be a: (1 Mark)
a. Parallelogram
b. Trapezium
c. Kite
d. Square
Q5: A diagonal of a parallelogram divides it into two congruent: (1 Mark)
a. Square
b. Parallelogram
c. Triangles
d. Rectangle
Q6: Write true and false against each of the given statements. (2 Marks)
(a) Diagonals of a rhombus are equal.
(b) Diagonals of rectangles are equal.
(c) Kite is a parallelogram.
(d) Sum of the interior angles of a triangle is 180°.
Q7: Three angles of a quadrilateral are 75º, 90º and 75º. The fourth angle is (2 Marks)
Q8: The angles of a quadrilateral are in the ratio 4: 5: 10: 11. The angles are: (2 Marks)
Q9: A diagonal of a rectangle is inclined to one side of the rectangle at 25º. Then find the acute angle between the diagonals. (3 Marks)
Q10: ABCD is a rhombus such that ∠ACB = 40º. Then find ∠ADB. (3 Marks)
Q11: In the given parallelogram ABCD, find the value of x and y. (3 Marks)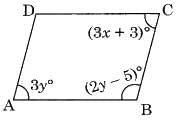
Q12: Find the values of x and y in the following parallelogram. (5 Marks)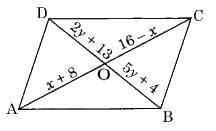
Q13: ABCD is a rhombus with ∠ABC = 126°, find the measure of ∠ACD. (5 Marks)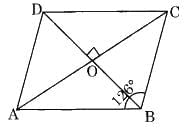
You can access the solutions to this Unit Test here.
The document Unit Test: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash) is a part of the Class 8 Course Mathematics Class 8- New NCERT (Ganita Prakash).
All you need of Class 8 at this link: Class 8
|
26 videos|177 docs|11 tests
|
FAQs on Unit Test: Quadrilaterals - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What are the key properties of quadrilaterals? |  |
Ans. Quadrilaterals are four-sided polygons with specific properties. The sum of the interior angles of any quadrilateral is 360 degrees. They can be classified into various types, such as squares, rectangles, trapezoids, and rhombuses, each with unique characteristics. For instance, in a rectangle, opposite sides are equal, while in a rhombus, all four sides are equal. Understanding these properties helps in solving geometric problems related to quadrilaterals.
| 2. How can we classify different types of quadrilaterals? | |
Ans. Quadrilaterals can be classified based on their sides and angles. The main types include:
- Parallelograms: Opposite sides are parallel and equal.
- Rectangles: All angles are right angles.
- Rhombuses: All sides are equal, and opposite angles are equal.
- Squares: All sides are equal, and all angles are right angles.
- Trapezoids: Only one pair of opposite sides is parallel.
This classification is essential for identifying and working with various quadrilateral properties in geometry.
| 3. What is the formula for finding the area of a quadrilateral? | |
Ans. The area of a quadrilateral can be calculated using different formulas depending on its type. For a rectangle, the area is calculated as length × width. For a square, it’s side². For a trapezoid, the area can be found using the formula area = 1/2 × (base₁ + base₂) × height. For irregular quadrilaterals, one can divide it into triangles or use the Brahmagupta's formula for cyclic quadrilaterals, which states that area = √(s(s-a)(s-b)(s-c)(s-d)), where s is the semi-perimeter and a, b, c, d are the sides.
| 4. What is the significance of the diagonals in quadrilaterals? | |
Ans. The diagonals of quadrilaterals have important properties. In parallelograms, the diagonals bisect each other. In rectangles, the diagonals are equal in length and bisect each other. In rhombuses, the diagonals bisect each other at right angles. Understanding the properties of diagonals helps in solving problems related to the shape and area of quadrilaterals and is crucial in coordinate geometry.
| 5. How is the concept of quadrilaterals important in real-life applications? | |
Ans. The concept of quadrilaterals is vital in various real-life applications, including architecture, engineering, and art. Architects use quadrilateral shapes to design buildings and structures, ensuring stability and aesthetic appeal. In engineering, quadrilateral shapes are often used in mechanical parts and structural designs. Additionally, artists utilize these shapes in creating visually appealing designs and patterns. Understanding quadrilaterals helps in making informed decisions in these fields.
About this Document
4.82/5
Rating
Oct 02, 2025
Last updated
Related Exams
Document Description: Unit Test: Quadrilaterals for Class 8 2025 is part of Mathematics Class 8- New NCERT (Ganita Prakash) preparation.
The notes and questions for Unit Test: Quadrilaterals have been prepared according to the Class 8 exam syllabus. Information about Unit Test: Quadrilaterals covers topics
like and Unit Test: Quadrilaterals Example, for Class 8 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Unit Test: Quadrilaterals.
Introduction of Unit Test: Quadrilaterals in English is available as part of our Mathematics Class 8- New NCERT (Ganita Prakash)
for Class 8 & Unit Test: Quadrilaterals in Hindi for Mathematics Class 8- New NCERT (Ganita Prakash) course.
Download more important topics related with notes, lectures and mock test series for Class 8
Exam by signing up for free. Class 8: Unit Test: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash)
Description
Full syllabus notes, lecture & questions for Unit Test: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash) - Class 8 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 8- New NCERT (Ganita Prakash) | Best notes, free PDF download
Information about Unit Test: Quadrilaterals
In this doc you can find the meaning of Unit Test: Quadrilaterals defined & explained in the simplest way possible. Besides explaining types of
Unit Test: Quadrilaterals theory, EduRev gives you an ample number of questions to practice Unit Test: Quadrilaterals tests, examples and also practice Class 8
tests
Related Searches
Unit Test: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash)
,past year papers
,practice quizzes
,Summary
,mock tests for examination
,MCQs
,Previous Year Questions with Solutions
,video lectures
,ppt
,Unit Test: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash)
,Exam
,Extra Questions
,Sample Paper
,Unit Test: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash)
,Free
,study material
,Objective type Questions
,Semester Notes
,shortcuts and tricks
,Viva Questions
,Important questions
;
Additional Information about Unit Test: Quadrilaterals for Class 8 Preparation
Unit Test: Quadrilaterals Free PDF Download
The Unit Test: Quadrilaterals is an invaluable resource that delves deep into the core of the Class 8 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Unit Test: Quadrilaterals now and kickstart your journey towards success in the Class 8 exam.
Importance of Unit Test: Quadrilaterals
The importance of Unit Test: Quadrilaterals cannot be overstated, especially for Class 8 aspirants.
This document holds the key to success in the Class 8 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Unit Test: Quadrilaterals Notes
Unit Test: Quadrilaterals Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Unit Test: Quadrilaterals.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Unit Test: Quadrilaterals Notes on EduRev are your ultimate resource for success.
Unit Test: Quadrilaterals Class 8 Questions
The "Unit Test: Quadrilaterals Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Unit Test: Quadrilaterals on the App
Students of Class 8 can study Unit Test: Quadrilaterals alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Unit Test: Quadrilaterals,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Unit Test: Quadrilaterals is prepared as per the latest Class 8 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup