Unit Test (Solutions): Lines and Angles | Mathematics for Class 6 PDF Download
Time: 1 hour
Maximum Marks: 30
Attempt all questions.
Question numbers 1 to 5 carry 1 mark each.
Question numbers 6 to 8 carry 2 marks each.
Question numbers 9 to 11 carry 3 marks each.
Question number 12 & 13 carry 5 marks each.
Q1: Measure the angle formed when the hour hand of a clock moves from 3 o’clock to 6 o’clock. (1 Mark)
Ans: 90°
The hour hand moves from 3 to 6, which covers 3 hours. Each hour represents 30°, so the total angle covered is 3 × 30° = 90°.
Q2: A ray starts at point M and passes through point N. If another point P is on the right of point N on the same line, what is the ray called using these points? (1 Mark)
Ans: Ray MP
A ray starts at a point (M in this case) and passes through another point (N), continuing indefinitely through point P, hence it is called Ray MP.
Q3: Construct a 40° angle using a protractor. (1 Mark)
Ans: 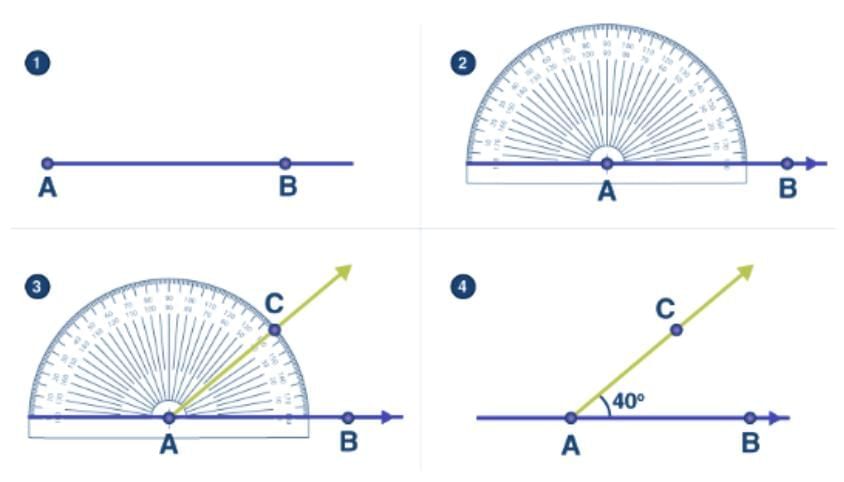
Q4: Identify the type of angle (acute, right, obtuse, or straight) that is formed by the hands of a clock at 10:00. (1 Mark)
Ans: Acute angle
At 10:00, the hour hand is on 10 and the minute hand is on 12.
The angle between each hour marking is 30°.
From 10 to 12 is 2 hour divisions: 2 × 30° = 60°
Since 60° is less than 90°, it is an acute angle.
Q5: What is the measure of an angle that is three times the measure of a right angle? (1 Mark)
Ans: 270°
A right angle is 90°. So, three times the right angle is 3 × 90° = 270°.
Q6: Two lines intersect and form an angle of 150°. What are the measures of all angles at the intersection? (2 Marks)
Ans: The angles are 150°, 30°, 150°, 30°.
Opposite angles are equal, so two of the angles are 150° and the other two are 30°, because 180° − 150° = 30°.
Q7: Draw a line segment of 5 cm. At its midpoint, draw a perpendicular line segment of 4 cm. What type of angle is formed between the two line segments? (2 Marks)
Ans: Right angle (90°)
A perpendicular line forms a right angle with the original line segment.
Q8: Can two obtuse angles be supplementary? Explain why or why not. (2 Marks)
Ans: No, two obtuse angles cannot be supplementary.
An obtuse angle is greater than 90°. The sum of two obtuse angles would exceed 180°, making them non-supplementary.
Q9: An angle bisector divides ∠XYZ into two angles, ∠XYB and ∠BYZ. If ∠XYZ = 90°, find ∠XYB and ∠BYZ. (3 Marks)
Ans: ∠XYB = 45°, ∠BYZ = 45°
The angle bisector divides ∠XYZ equally into two angles, so each is 90° ÷ 2 = 45°.
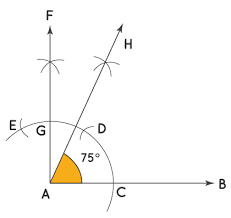
Q10: Construct an angle of 75° using a protractor and label it ∠ABC. Describe the steps taken. (3 Marks)
Ans:
Step 1: Draw a ray AB. With A as the center and any radius, draw an arc that cuts AB at C.
Step 2: With C as the center and the same radius, we draw an arc cutting the first arc at D, and with D as the center and the same radius, draw an arc that cuts the first arc at E
Step 3: With E and D as centers and with the same radius, we draw two arcs cutting each other at F. Join AF. The line AF makes 90° with the line segment AB.
Step 4: Mark the point where the line AF touches the semi-circular arc as G. Now with G and D as centers, draw two arcs again cutting each other at H. Now we join AH. ∠HAB= 75°.
The construction of an angle of 75° is shown below.
.
Q11: Use a protractor to find the measure of each angle. Then classify each angle as acute, obtuse, right, or reflex. (5 Marks)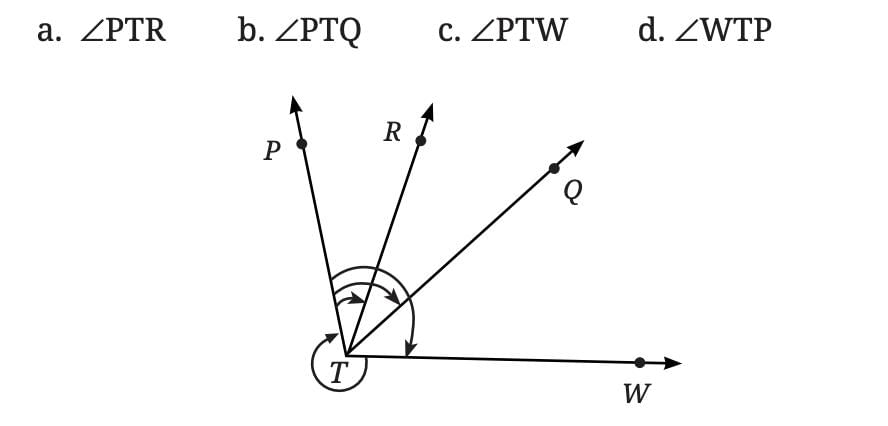 Ans: (a) ∠PTR = 300 reflex
Ans: (a) ∠PTR = 300 reflex
(b) ∠PTQ = 60° acute
(c) ∠PTW = 105° obtuse
(d) ∠WTP = 225° reflex
Q12: A triangle has angles in the ratio 1:2:3. Find the measures of all three angles. (5 Marks)
Ans: 30°, 60°, 90°
Let the angles be x, 2x, and 3x. The sum of the angles in a triangle is 180°. So,
x + 2x + 3x = 180°
⇒ 6x = 180°
⇒ x = 30°
Thus, the angles are 30°, 60°, and 90°.
Q13: Given two parallel lines cut by a transversal with one pair of corresponding angles as 110∘, find all other angles formed by the transversal. (5 Marks)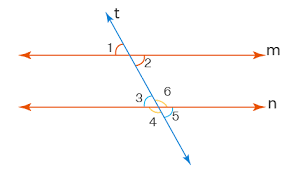
Ans: In the given figure, lines m and n are parallel, and line t is a transversal. The question specifies that one pair of corresponding angles is 110°.
Given the figure: Angle 2 corresponds with angle 6, assuming angle 2 is the 110° angle as per the original question.
Angle 2 and Angle 6 = 110° (corresponding angles)
Angle 1 = 110° (vertically opposite angle to angle 2)
Angle 3 = 70° (linear pair with angle 2)
Angle 5 = 70° (corresponding angle to angle 3)
Angle 4 = 70° (vertically opposite to angle 5)
Thus, you have:
Angle 1 = 110°
Angle 2 = 110°
Angle 3 = 70°
Angle 4 = 70°
Angle 5 = 70°
Angle 6 = 110°
These calculations ensure all angles formed by the transversal with the two parallel lines are consistent with the geometric rules of corresponding, alternate, and vertically opposite angles.
|
48 videos|389 docs|23 tests
|
FAQs on Unit Test (Solutions): Lines and Angles - Mathematics for Class 6
| 1. What are the basic properties of lines and angles that I should know for the exam? |  |
| 2. How do I calculate the measure of an angle when given other angles? |  |
| 3. What types of questions can I expect on the unit test about lines and angles? |  |
| 4. How can I effectively prepare for the lines and angles section of the unit test? |  |
| 5. What resources can I use to study lines and angles further? |  |

















