Class 10 Maths Chapter 2 Question Answers - Polynomials
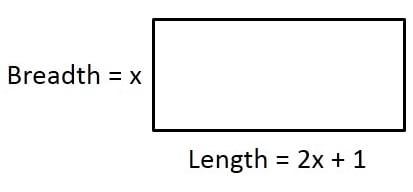
Ques 1: A charity trust decides to build a prayer hall having a carpet area of 300 square metres with its length one metre more than twice its breadth.
(i) Find the length and the breadth of the hall.
(ii) Which mathematical concept is used in the above problem?
(iii) By building a prayer hall, whose value is depicted by the trust?
Sol:
(i) Let the breadth of the hall = x metres
∴ Length of the hall
= 2 [Breadth of the hall] + 1 metre
= (2x + 1) metre
∴ Carpet area of the hall= Length × Breadth
= (2x + 1) × x
= 2x2 + x
But the carpet area of the hall = 300 sq. metre
∴ 2x2 + x = 300
⇒ 2x2 + x – 300 = 0
⇒ 2x2 + 25x – 24x – 300 = 0
⇒ x(2x + 25) –12(2x + 25) = 0
⇒ (x – 12) (2x + 25) = 0
⇒ x – 12 = 0
or 2x + 25 = 0
⇒x = 12
or x = - 252But x = - 252 is not required as the length
or breadth cannot be negative.
∴ x = 12 m and 2x + 1 = (2 × 12) + 1 = 25 m
∴ Breadth of the hall = 12 m
Length of the hall = 25 m
(ii) Quadratic equations
(iii) Enhancing prayer and God fearing feelings.
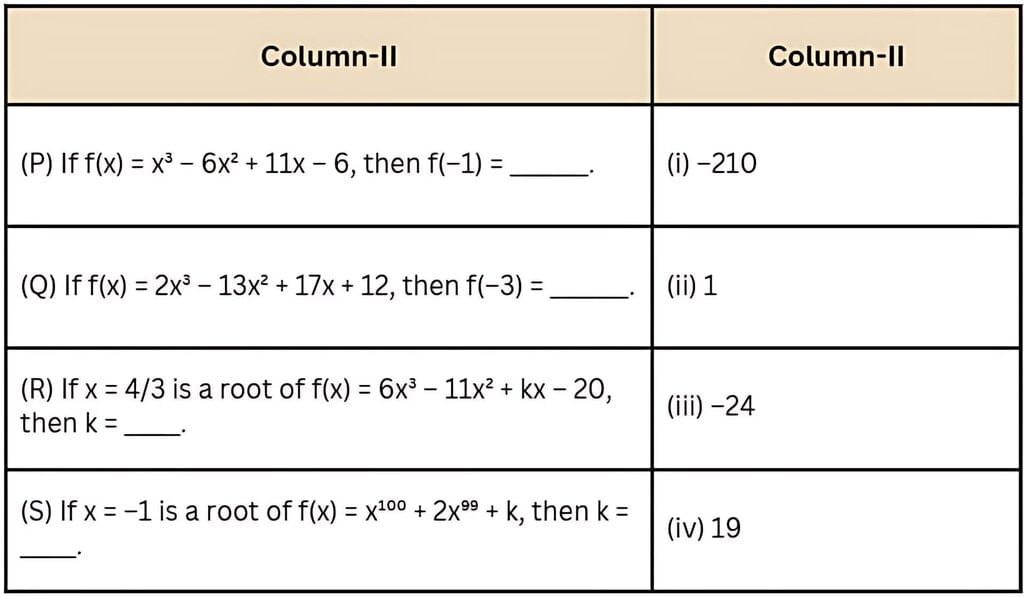
Q2. Match the following,
Sol:
(P)
f(x) = x³ − 6x² + 11x − 6.
Find f(−1):
f(−1) = (−1)³ − 6(−1)² + 11(−1) − 6
= −1 − 6 − 11 − 6
= −24.
So, P → −24 (matches (iii)).(Q)
f(x) = 2x³ − 13x² + 17x + 12.
Find f(−3):
f(−3) = 2(−3)³ − 13(−3)² + 17(−3) + 12
= 2(−27) − 13(9) − 51 + 12
= −54 − 117 − 51 + 12
= −210.
So, Q → −210 (matches (i))(R)
Given x = 4/3 is a root of f(x) = 6x³ − 11x² + kx − 20.
A “root” means f(4/3) = 0. Substitute x = 4/3:
6(4/3)³ − 11(4/3)² + k(4/3) − 20 = 0
6·64/27 − 11·16/9 + 4k/3 − 20 = 0
= 128/9 − 176/9 + 4k/3 − 20 = 0
= (−48/9) + 4k/3 − 20 = 0
= (−16/3) + 4k/3 − 20 = 0.
Multiply everything by 3 to clear denominators:
−16 + 4k − 60 = 0 ⇒ 4k − 76 = 0 ⇒ k = 19.
So, R → 19 (matches (iv))
(S)Given x = −1 is a root of f(x) = x¹⁰⁰ + 2x⁹⁹ + k.
So f(−1) = 0:(−1)¹⁰⁰ + 2(−1)⁹⁹ + k = 0
1 − 2 + k = 0 ⇒ k = 1.
So, S → 1 (matches (ii)).
Q3. Santosh has ₹ (x³ – 3x² + 4x + 50). He want to buy chocolates each of cost ₹ (x – 3). After buying maximum number of chocolates with his money, how much money is left with him?
Sol:
Step 1: Understand the question
Total money Santosh has: M = x³ – 3x² + 4x + 50
Cost of 1 chocolate: C = x – 3
We need to find remainder money after buying maximum chocolates. This means we have to divide the total money by the cost of one chocolate and see what is left (the remainder).Step 2: Use polynomial division
We divide x³ – 3x² + 4x + 50 by x – 3.
After using long division method , we get
So, x³ – 3x² + 4x + 50 = (x – 3)(x² + 4) + 62Step 3: Interpret remainder
The remainder 62 is the money left after buying the maximum number of chocolates.
Q4. Area of a rectangular field is (2x³ − 11x² − 4x + 5) sq. units and side of a square field is (2x² + 4) units. Find the difference between their areas (in sq. units).
Sol: Area of the square = (2x² + 4)² = 4x⁴ + 16x² + 16.
Area of the rectangle = 2x³ − 11x² − 4x + 5.
Difference = square area − rectangle area
= (4x⁴ + 16x² + 16) − (2x³ − 11x² − 4x + 5)
= 4x⁴ − 2x³ + 27x² + 4x + 11
Q5. Length, breadth and height of a cuboidal tank are (x − 3y) m, (x + 3y) m and (x² + 9y²) m respectively. Find the volume of the tank.
Sol: Volume = length × breadth × height
= (x − 3y)(x + 3y)(x² + 9y²)
= (x² − 9y²)(x² + 9y²) [using (a − b)(a + b) = a² − b²]
= x⁴ − 81y⁴.
|
127 videos|692 docs|84 tests
|
FAQs on Class 10 Maths Chapter 2 Question Answers - Polynomials
| 1. What are polynomials and how are they classified? |  |
| 2. How do you add and subtract polynomials? |  |
| 3. What is the importance of the degree of a polynomial? |  |
| 4. How can polynomials be factored? |  |
| 5. What are real-world applications of polynomials? |  |