Value of Polynomial and Division Algorithm - 2 | Algebra - Mathematics PDF Download
Factor Theorem
In this part, we will look at the Factor Theorem, which uses the remainder theorem and learn how to factorise polynomials. Further, we will be covering the splitting method and the factor theorem method.

If p(x) is a polynomial of degree n > 1 and a is any real number, then
- x – a is a factor of p(x), if p(a) = 0, and
- p(a) = 0, if x – a is a factor of p(x).
Let’s look at an example to understand this theorem better.
Example: Examine whether x + 2 is a factor of x3 + 3x2 + 5x + 6.
Solution: To begin with, we know that the zero of the polynomial (x + 2) is –2. Let p(x) = x3 + 3x2 + 5x + 6
Then, p(–2) = (–2)3 + 3(–2)2 + 5(–2) + 6 = –8 + 12 – 10 + 6 = 0
According to the factor theorem, if p(a) = 0, then (x – a) is a factor of p(x). In this example, p(a) = p(- 2) = 0
Therefore, (x – a) = {x – (-2)} = (x + 2) is a factor of ‘x3 + 3x2 + 5x + 6’ or p(x).
Factorisation of polynomials
You can factorise polynomials by splitting the middle term as follows: to begin with, consider a polynomial ax2 + bx + c with factors (px + q) and (rx + s). Therefore, we have ax2 + bx + c = (px + q) (rx + s). So, ax2 + bx + c = prx2 + (ps + qr) x + qs
If we compare the coefficients of x2, we get a = pr. Also, on comparing the coefficients of x, we get b = ps + qr. Finally, on comparing the constants, we get c = qs. Hence, b is the sum of two numbers ‘ps’ and ‘qr’, whose product is (ps)(qr) = (pr)(qs) = ac.
Therefore, to factorise ax2 + bx + c, we have to write b as the sum of two numbers whose product is ‘ac’. Let’s look at an example to understand this clearly.
Example
Factorise 6×2 + 17x + 5 by splitting the middle term.
Solution 1 (By splitting method): As explained above, if we can find two numbers, ‘p’ and ‘q’ such that, p + q = 17 and pq = 6 x 5 = 30, then we can get the factors.
After looking at the factors of 30, we find that numbers ‘2’ and ‘15’ satisfy both the conditions, i.e. p + q = 2 + 15 = 17 and pq = 2 x 15 = 30. So,
6x2 + 17x + 5 = 6x2 + (2 + 15)x + 5
= 6x2 + 2x + 15x + 5
= 2x(3x + 1) + 5(3x + 1)
= (3x + 1) (2x + 5)
Therefore, the factors of (6x2 + 17x + 5) are (3x + 1) and (2x + 5) with a remainder, zero.
Example
Factorise y2 – 5y + 6 by using the Factor Theorem.
Solution: Let p(y) = y2 – 5y + 6. Now, if p(y) = (y – a) (y – b), the constant term will be ab as can be seen below,
p(y) = (y – a)(y – b)
= y2 – by – ay + ab
On comparing the constants, we get ab = 6. Next, the factors of 6 are 1, 2 and 3. Now, p(2) = 22– (5 × 2) + 6 = 4 – 10 + 6 = 0. So, (y – 2) is a factor of p(y). Also, p(3) = 32 – (5 × 3) + 6 = 9 – 15 + 6 = 0. So, (y – 3) is also a factor of y2 – 5y + 6. Therefore, y2 – 5y + 6 = (y – 2)(y – 3)
More Solved Examples for You
Question: Factorise x3 – 23x2 + 142x – 120
Solution: Let p(x) = x3 – 23x2 + 142x – 120. To begin with, we will start finding the factors of the constant ‘– 120’, which are:
±1, ±2, ±3, ±4, ±5, ±6, ±8, ±10, ±12, ±15, ±20, ±24, ±30, ±40, ±60 and ±120
Further, by trial, we find that p(1) = 0. Hence, we conclude that (x – 1) is a factor of p(x). Also, we see that
[x3 – 23x2 + 142x – 120] = x3 – x2 – 22x2 + 22x + 120x – 120
So, by removing the common factors, we have x3 – 23x2 + 142x – 120 = x2(x –1) – 22x(x – 1) + 120(x – 1)
Further, taking ‘x – 1’ common, we get x3 – 23x2 + 142x – 120 = (x – 1) (x2 – 22x + 120)
Therefore, x3 – 23x2 + 142x – 120 = (x – 1) (x2 – 22x + 120)
Also, note that if we divide p(x) by ‘x – 1’, then the result will be (x2 – 22x + 120)
Going on, x2 – 22x + 120 can be factorised further. So, by splitting the middle term, we get:
x2 – 22x + 120 = x2 – 12x – 10x + 120 … [ (– 12 – 10 = – 22) and {(–12)( –10) = 120}]
= x(x – 12) – 10(x – 12)
= (x – 12) (x – 10)
Therefore, we have x3 – 23x2 – 142x – 120 = (x – 1)(x – 10)(x – 12)
Question: Factorise x3 – 2x2 – x + 2
Solution: Let p(x) = x3 – 2x2 – x + 2. To begin with, we will start finding the factors of the constant ‘2’, which are: 1, 2
By trial, we find that p(1) = 0. Hence, we conclude that (x – 1) is a factor of p(x).
So, by removing the common factors, we have x3 – 2x2 – x + 2 = x2(x – 2) – (x – 2) = (x2– 1)(x – 2)
= (x + 1)(x – 1)(x – 2) … [Using the identity (x2 – 1) = (x + 1)(x – 1)]
Therefore, the factors of x3 – 2x2 – x + 2 are (x + 1), (x – 1) and (x – 2)
Geometrical Representation of Zeroes of a Polynomial
In the study of polynomials, you are aware that a real number ‘k’ is a zero of the polynomial p(x) if p(k) = 0. Remember, zero of a polynomial is different from a zero polynomial. We have seen the Remainder theorem use the concept of zeroes of a polynomial too. In order to understand their importance, we will look at the geometrical representations of linear and quadratic polynomials and the geometrical meaning of their zeroes.
Linear Polynomial
Let’s look at a linear polynomial ax + b, where a ≠ 0. You have already studied that the graph of y = ax + b is a straight line. Let’s look at the graph of y = 2x + 3.

The straight line y = 2x + 3 will pass through the points (- 2, – 1) and (2, 7). Here is how the graph looks like:
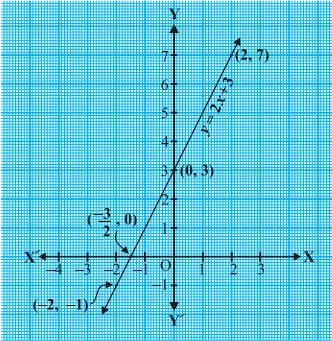
Fig. 1
From the Fig.1 above, you can see that the graph of y = 2x + 3 intersects the x-axis at the point (- 3/2, 0). Now, the zero of (2x + 3) is (- 3/2). Therefore, the zero of the linear polynomial (2x + 3) is the x-coordinate of the point where the graph of y = 2x + 3 intersects the x-axis. Hence, we can say,
For a linear polynomial ax + b, a ≠ 0, the graph of y = ax + b is a straight line which intersects the x-axis at exactly one point, namely, (- b/a, 0). Also, this linear polynomial has only one zero which is the x-coordinate of the point where the graph of y = ax + b intersects the x-axis.
Quadratic Polynomial
Let’s look at a quadratic polynomial, x2 – 3x – 4. To look at the graph of y = x2 – 3x – 4, let’s list some values:
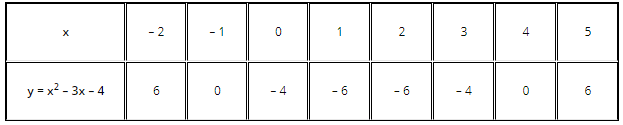
The graph of y = x2 – 3x – 4 will pass through (- 2, 6), (- 1, 0), (0, – 4), (1, – 6), (2, – 6), (3, – 4), (4, 0) and (5, 6). Here is how the graph looks:
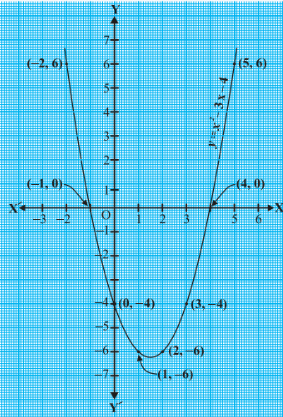
Fig.2
For that matter, for any quadratic polynomial y = ax2 + bx + c, a ≠ 0, the graph of y = ax2 + bx + c has either one of these two shapes:
- If a > 0, then it is open upwards like the one shown in the graph above
- If a < 0, then it is open downwards.
These curves are parabolas. A quick look at the table above shows that (- 1) and (4) are zeroes of the quadratic polynomial. From the Fig. 2 above, you can see that (- 1) and (4) are the x-coordinates of the points where the graph of y = x2 – 3x – 4 intersects the x-axis. Therefore, we can say,
As far as the shape of the graph is concerned, the following three cases are possible:
Case (i)
The graph cuts x-axis at two distinct points A and A′, where the x-coordinates of A and A′ are the two zeroes of the quadratic polynomial ax2 + bx + c, as shown below:
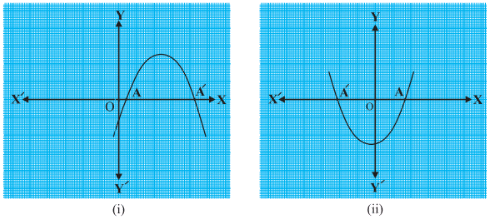
Fig.3
Case (ii)
The graph intersects the x-axis at only one point, or at two coincident points. Also, the x-coordinate of A is the only zero for the quadratic polynomial ax2 + bx + c, as shown below:
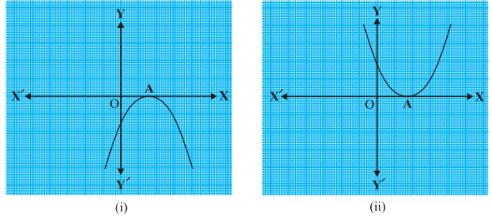
Fig.4
Case (iii)
The graph is either
- Completely above the x-axis or
- Completely below the x-axis.
So, it does not cut the x-axis at any point. Hence, the quadratic polynomial ax2 + bx + c has no zero, as shown below:
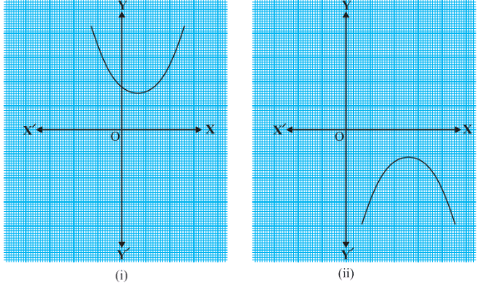
Fig.5
To summarize, a quadratic polynomial can have either:
- Two distinct zeroes (as shown in Case i)
- Two equal zeroes (or one zero as shown in Case ii)
- No zero (as shown in Case iii)
It can also be summarized by saying that a polynomial of degree 2 has a maximum of 2 zeroes.
Cubic Polynomial
Let’s look at a cubic polynomial, x3 – 4x. Next, let’s list a few values to plot the graph of y = x3 – 4x.
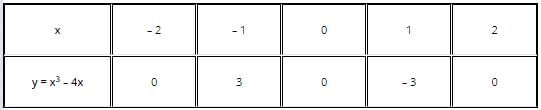
The graph of y = x3 – 4x will pass through (- 2, 0), (- 1, 3), (0, 0), (1, – 3), and (2, 0). Here is how the graph looks like:
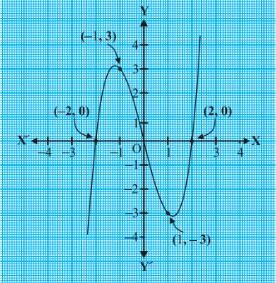
Fig.6
From the table above, we can see that 2, 0 and – 2 are the zeroes of the cubic polynomial x3 – 4x. You can also observe that the graph of y = x3 – 4x intersects the x-axis at 2, 0 and -
2. Let’s take a quick look at some examples:
Let’s plot the graph of the following two cubic polynomials:
- x3
- x3 – x2
The graphs of y = x3 and y = x3 – x2 look as follows:
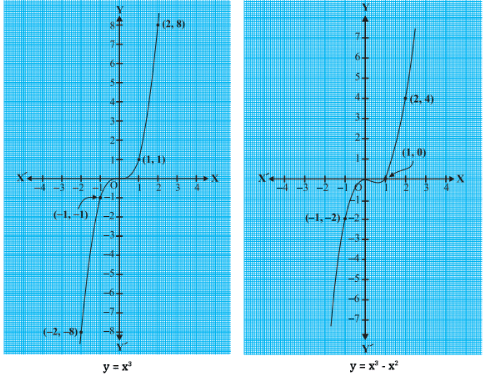
Fig.7
From the first graph, you can observe that 0 is the only zero of the polynomial x3, since the graph of y = x3 intersects the x-axis only at 0. Similarly, the polynomial x3 – x2 = x2(x – 1) has two zeroes, 0 and 1. From the second diagram, you can see that the graph of y = x3 – x2 intersects the x-axis at 0 and 1.
Hence, we can conclude that there is a maximum of three zeroes for any cubic polynomial. Or, any polynomial with degree 3 can have maximum 3 zeroes. In general,
Given a polynomial p(x) of degree n, the graph of y = p(x) intersects the x-axis at a maximum of n points. Therefore, a polynomial p(x) of degree n has a maximum of n zeroes.
Solved Examples for You
Question: The graphs of y = p(x) are given in the figure below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.
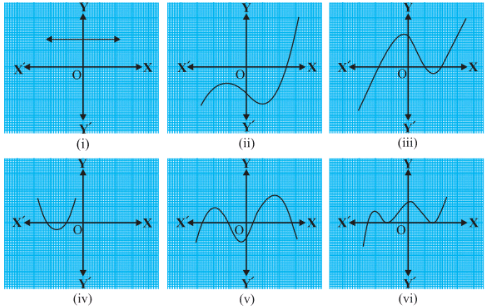
Fig.8
Solution: The number of zeroes in each of the graphs above are:
- 0, since the line is not intersecting the x-axis.
- 1, since the line intersects the x-axis once.
- 2, since the line intersects the x-axis twice.
- 2, since the line intersects the x-axis twice.
- 4, since the line intersects the x-axis four times.
- 3, since the line intersects the x-axis thrice.
|
161 videos|58 docs
|
FAQs on Value of Polynomial and Division Algorithm - 2 - Algebra - Mathematics
| 1. What is the value of a polynomial? |  |
| 2. How is the value of a polynomial calculated? |  |
| 3. What is the Division Algorithm in mathematics? |  |
| 4. How is the Division Algorithm applied to polynomials? |  |
| 5. Why is the Division Algorithm important in polynomial division? |  |






















