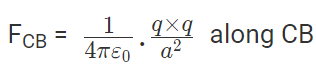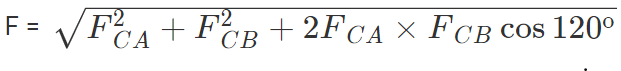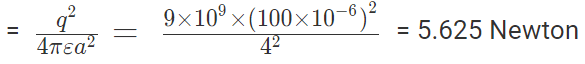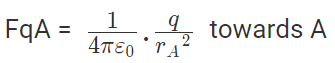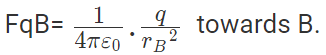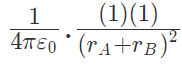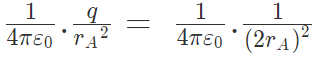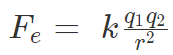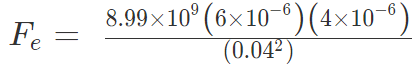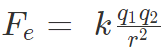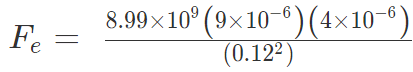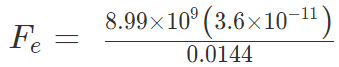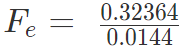Coulomb's Law | Physics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
What is Coulomb’s Law?
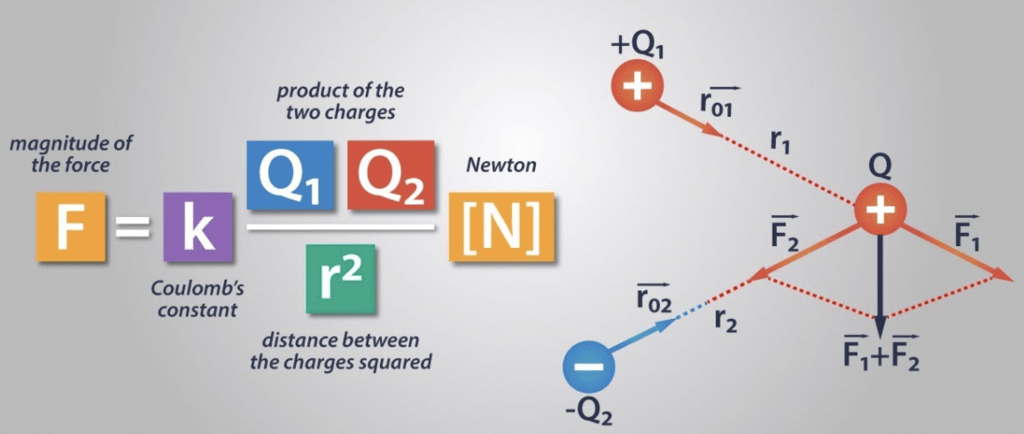
According to Coulomb’s law, the force of attraction or repulsion between two charged bodies is directly proportional to the product of their charges and inversely proportional to the square of the distance between them. It acts along the line joining the two charges considered to be point charges.
 Coulomb's Law Formula
Coulomb's Law Formula
History of Coulomb’s Law
A French physicist Charles Augustin de Coulomb in 1785 coined a tangible relationship in mathematical form between two bodies that have been electrically charged. He published an equation for the force causing the bodies to attract or repel each other which is known as Coulomb’s law or Coulomb’s inverse-square law.
Vector Form of Coulomb’s Law
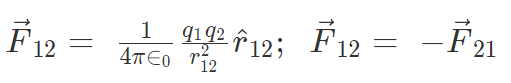 Here F12 is the force exerted by q1 on q2 and F21 is the force exerted by q2 on q1.
Here F12 is the force exerted by q1 on q2 and F21 is the force exerted by q2 on q1.
Coulomb’s law holds for stationary charges only which are point sized. This law obeys Newton’s third law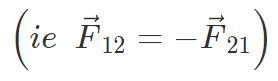
Force on a charged particle due to a number of point charges is the resultant of forces due to individual point charges i.e.
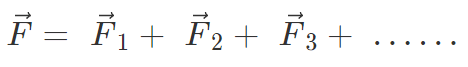
What is 1 Coulomb of Charge?
A coulomb is that charge which repels an equal charge of the same sign with a force of 9 × 109 N, when the charges are one meter apart in a vacuum. Coulomb force is the conservative mutual and internal force.
The value of εo is 8.86 × 10-12 C2/Nm2 (or) 8.86 × 10-12 Fm–1Note: Coulomb force is true only for static charges.
Conditions for Stability
If q is slightly displaced towards A, FA increases in magnitude while FB decreases in magnitude. Now the net force on q is toward A so it will not return to its original position. So for axial displacement, the equilibrium is unstable.
If q is displaced perpendicular to AB, the force FA and FB bring the charge to its original position. So for perpendicular displacement, the equilibrium is stable.
Limitations of Coulomb’s Law
- The law is applicable only for the point charges at rest.
- Coulomb’s Law can be only applied in those cases where the inverse square law is obeyed.
- It is difficult to implement Coulomb’s law where charges are in arbitrary shape because in such cases we cannot determine the distance’ between the charges.
- The law can’t be used directly to calculate the charge on the big planets.
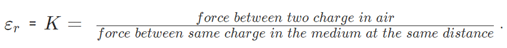
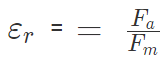
- For air K = 1
- For metals K = infinity
The force between 2 charges depends upon the nature of the intervening medium, whereas gravitational force is independent of the intervening medium.
For air or vacuum, 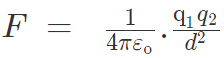 since for air or vacuum, εr = K = 1
since for air or vacuum, εr = K = 1
The value of 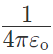 is equal to 9 × 109 Nm2/C2.
is equal to 9 × 109 Nm2/C2.
Application of The Coulombs Law
- To calculate the distance and force between the two charges.
- The electric field can be calculated using the coulombs law
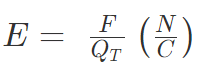
Where E = Strength of the electric field
F = Electrostatic force
QT = Test charge in coulombs
- To calculate the force on one point due to the presence of several points (Theorem of superposition).
Key Points on Coulomb’s Law
1. If the force between two charges in two different media is the same for different separations,  = constant.
= constant.
2. Kr2 = constant or K1r12 = K2r22
3. If the force between two charges separated by a distance ‘r0’ in a vacuum is the same as the force between the same charges separated by a distance ‘r’ in a medium, then from Coulomb’s Law; Kr2 = r02
4. Two identical conductors having charges q1 and q2 are put to contact and then separated after which each will have a charge equal to q1 + q2/2. If the charges are q1 and – q2, then each will have a charge equal to q1 - q2/2.
5. Two spherical conductors having charges q1 and q2 and radii r1 and r2 are put to contact and then separated the charges of the conductors after contact is;
q1 = [r1/(r1 + r2)] (q1 + q2) and q2 = [r2/(r1 + r2)] (q1 + q2)
6. If the force of attraction or repulsion between two identical conductors having charges q1 and q2 when separated by a distance d is F. Also if they are put to contact and then separated by the same distance the new force between them is
7. If charges are q1 and -q2 then, F = F(q1 + q2)2 / 4q1q2
8. Between two electrons separated by a certain distance: Electrical force/Gravitational force = 1042
9. Between two protons separated by a certain distance: Electrical force/Gravitational force = 1036
10. Between a proton and an electron separated by a certain distance: Electrical force/Gravitational force = 1039
11. The relationship between the velocity of light, the permeability of free space and permittivity of free space is given by the expression c = 1 / √ (μoεo)
12. If Coulomb’s law is applied to two identical balls of mass m are hung by silk thread of length ‘l’ from the same hook and carry similar charges q then;
- The distance between balls =
- The tension in the thread =
- If the total system is kept in space then the angle between threads is 180° and tension in a thread is given by
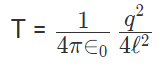
- A charge Q is divided into q and (Q – q). Then electrostatic force between them is maximum when
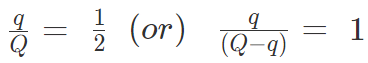
Solved Examples on Coulomb's Law
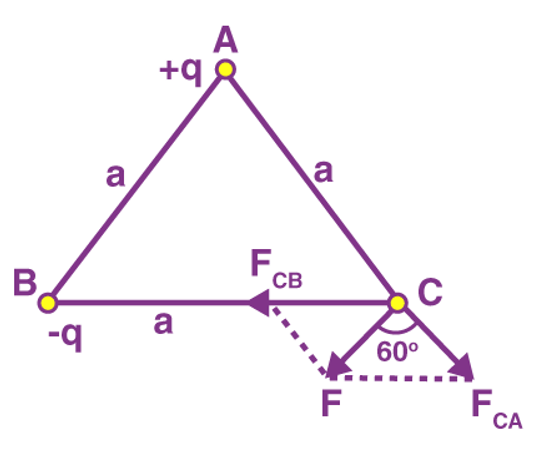
Example 1: Charges of magnitude 100 microcoulomb each are located in vacuum at the corners A, B and C of an equilateral triangle measuring 4 meters on each side. If the charge at A and C are positive and the charge B negative, what is the magnitude and direction of the total force on the charge at C?
The situation is shown in fig. Let us consider the forces acting on C due to A and B.
Now, from Coulomb’s law, the force of repulsion on C due to A i.e., FCA in direction AC is given by
The force of attraction on C due to B i.e., FCB in direction CB is given by
Thus the two forces are equal in magnitude. The angle between them is 120º. The resultant force F is given by
This force is parallel to AB.
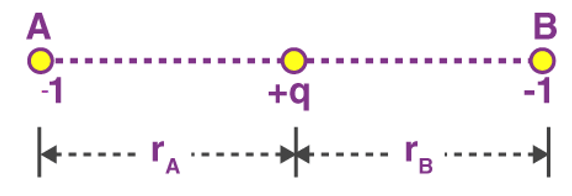
Example 2: The negative point charges of unit magnitude and a positive point charge q are placed along the straight line. At what position and for what value of q will the system be in equilibrium? Check whether it is stable, unstable or neutral equilibrium.
The two negative charges A and B of unit magnitude are shown in fig. Let the positive charge q be at a distance rA from A and at a distance rB from B.
Now, from coulombs law, Force on q due to A
Force on q due to B
These two forces acting on q are opposite and collinear. For the equilibrium of q, the two forces must also be equal i.e.
|FqA| = |FqB|
orHence rA = rB
So for the equilibrium of q, it must be equidistant from A & B i.e. at the middle of AB Now for the equilibrium of the system, A and B must be in equilibrium. For the equilibrium of A
Force on A by q =towards q
Force on A by B =away from q
The two forces are opposite and collinear. For equilibrium the forces must be equal, opposite and collinear. Hence
or q = 1/4 in magnitude of either charge.
It can also be shown that for the equilibrium of B, the magnitude of q must be 1/4 of the magnitude of either charge.
Example 3: A positive charge of 6 × 10-6 C is 0.040m from the second positive charge of 4 × 10-6 C. Calculate the force between the charges.
Given
q1 = 6 × 10-6 C
q2 = 4 × 10-6 C
r = 0.040 m
Fe = 134.85 N
Example 4: Two-point charges, q1 = +9 μC and q2 = 4 μC, are separated by a distance r = 12 cm. What is the magnitude of the electric force?
given
k = 8.988 x 109 Nm2C−2
q1 = 9 ×10-6 C
q2 = 4 ×10-6 C
Fe = 22.475 N
|
201 videos|410 docs|280 tests
|
FAQs on Coulomb's Law - Physics for Airmen Group X - Airforce X Y / Indian Navy SSR
| 1. What is Coulomb's Law? |  |
| 2. What is the formula for Coulomb's Law? |  |
| 3. What is the significance of Coulomb's constant in Coulomb's Law? |  |
| 4. How does Coulomb's Law explain the behavior of charged particles? |  |
| 5. What are the limitations of Coulomb's Law? |  |